Par exemple : Calculez une distribution qui corresponde au modèle de la loi Normale DdP (Normal Pdf).
| 1. | Cliquez sur la cellule de formule (deuxième cellule en partant du haut) de la colonne A. |
| 2. | Cliquez sur Statistiques > Distributions > Normal DdP pour sélectionner le modèle de distribution. |
La boîte de dialogue Normal DdP affiche alors des champs pour la saisie ou la sélection des arguments du calcul.
| 3. | Appuyez sur Tab autant de fois que nécessaire pour passer d’un champ à l’autre et fournir chaque argument. Vous pouvez entrer les valeurs ou les sélectionner dans la liste déroulante : |
| - | Valeur de X : Cliquez sur la flèche déroulante pour choisir une liste dans l’activité afin de fournir les valeurs de x nécessaires au calcul. |
| - | Moyenne : Entrez une valeur pour la moyenne ou cliquez sur la flèche déroulante pour choisir une variable qui contienne cette valeur. |
| - | Écart type : Entrez une valeur pour l’écart type ou sélectionnez une variable qui contienne cette valeur. |
| 4. | Cochez la case Dessin pour voir la distribution tracée dans l'application Données & statistiques. |
Remarque : l’option de dessin n’est pas disponible pour toutes les distributions.
| 5. | Cliquez sur OK. |
L’application Tableur & listes insère deux colonnes : la première affichant les noms des résultats et la seconde les valeurs correspondantes Les résultats sont représentés graphiquement dans l'application Données & statistiques.
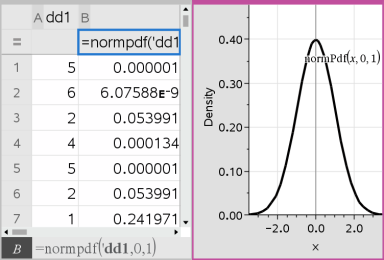
Remarque : les résultats sont liés aux données sources. Par exemple, si vous modifiez une valeur de la colonne A, l’équation est automatiquement actualisée.
Les distributions suivantes sont accessibles depuis l'application Tableur & listes. Pour plus d’informations sur ces fonctions, consultez le Manuel de l’utilisateur TI-Nspire™.
| • | Pour retourner un seul résultat de distribution basé sur une valeur unique, entrez la fonction dans une seule cellule. |
| • | Pour retourner une liste de résultats de distribution basée sur une liste de valeurs, entrez la fonction dans une cellule de formule de colonne. Dans ce cas, spécifiez une liste (colonne) qui contient les valeurs. Pour chaque valeur de la liste, la fonction de distribution retourne le résultat correspondant. |
Remarque : Pour les fonctions de distribution qui prennent en charge l'option de dessin (normPDF, tPDF, χ²Pdf et FPdf), cette option n’est disponible que si vous saisissez la fonction de distribution dans une cellule de formule.
Normal DdP (normPdf)
Calcule la densité de probabilité (DdP) de la distribution de la loi normale à la valeur x spécifiée. Les valeurs par défaut sont une moyenne μ= 0 et l’écart-type σ= 1. La densité de probabilité (DdP) est :
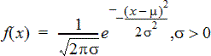
Cette distribution permet de déterminer la probabilité qu’une variable suivant une loi normale prenne une valeur particulière. L’option de dessin est disponible lorsque la fonction Normal DdP (Normal PDF) est invoquée depuis une cellule de formule.
Lorsque vous accédez aux distributions depuis la cellule de formule, vous devez sélectionner une liste valide dans le menu déroulant pour éviter des résultats inattendus. Si vous y accédez depuis une cellule de formule, vous devez spécifier un nombre pour la valeur de x. La distribution retourne la probabilité selon laquelle une variable prendra la valeur spécifiée.
Normal FdR (normCdf)
Calcule la probabilité qu’une variable suivant la loi normale de moyenne µ (valeur par défaut = 0) et d’écart type s (valeur par défaut = 1) prenne des valeurs entre la borne inférieure et la borne supérieure. Vous pouvez cocher la case Dessiner (Ombrer la zone) pour ombrer la zone qui se trouve entre les bornes inférieure et supérieure. Les modifications apportées à la borne inférieure et à la borne supérieure initiales sont automatiquement appliquées à la distribution.
Cette distribution permet de déterminer la probabilité qu’une variable suivant une loi normale prenne des valeurs entre deux bornes supérieure et inférieure. Elle est équivalente au calcul de l’aire de la région sous la courbe de la fonction de répartition d’une loi normale spécifiée entre les bornes.
Inverse Normale (invNorm)
Calcule la valeur de l’inverse de la fonction de répartition de la loi normale de paramètres m et s pour une aire donnée sous la courbe de distribution normale spécifiée par la moyenne µ et l’écart type s.
Cette fonction permet de déterminer la valeur de x pour laquelle la fonction de répartition de la loi normale prend la valeur area comprise entre 0 et x<1.
tDdP (tPdf)
Calcule la densité de probabilité (DdP) de la loi de Student t en une valeur spécifiée de x.df (degrés de liberté), df doit être > 0. La fonction de densité de probabilité (DdP) est :
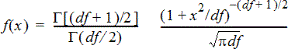
Cette distribution permet de déterminer la probabilité de l’occurrence d’une valeur lorsque l’écart type de population est inconnu et que la taille de l’échantillon est réduite. L’option de dessin est disponible lorsque la fonction t DdP est invoquée depuis une cellule de formule.
t FdR (tCdf)
Calcule la fonction de répartition de la loi de Student-t entre la borne inférieure et la borne supérieure pour les df (degrés de liberté) spécifiés. Vous pouvez cocher la case Dessiner (Ombrer la zone) pour ombrer la zone qui se trouve entre les bornes inférieure et supérieure. Les modifications apportées à la borne inférieure et la borne supérieure initiales sont automatiquement appliquées à la distribution.
Cette fonction permet de calculer la probabilité qu’une variable normalement répartie prenne des valeurs entre deux bornes pour une population normalement distribuée, lorsque l’écart type de population est inconnu.
Inverset t (invt)
Calcule l’inverse de la fonction de répartition de Student t de degrés de liberté df, pour une zone donnée sous la courbe.
Cette fonction permet de déterminer la valeur x pour laquelle la probabilité que la variable prenne des valeurs comprises entre 0 et x<1. Cette fonction est utilisée lorsque la moyenne et/ou l’écart-type de la population n’est pas connu(e).
c2 Pdf (c2 Pdf())
Calcule la fonction de densité de probabilité (DdP) pour la distribution c2 (chi-deux) pour une valeur x spécifiée. df (degrés de liberté), df doit être un entier > 0. La fonction de densité de probabilité (DdP) est :
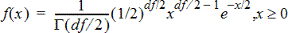
Cette distribution permet de déterminer la probabilité qu’une variable prenne une valeur dans une population suivant une loi du c2. L’option de dessin est disponible lorsque la fonction c2 Pdf est invoquée depuis une cellule de formule.
c2 FdR (c2 FdR())
Cette fonction calcule la probabilité qu’une variable suivant une loi du c2 (chi-deux) prenne une valeur entre les bornes lowBound et upBound pour la valeur df (degrés de liberté) spécifiée. Vous pouvez cocher la case Dessiner (Ombrer la zone) pour ombrer la zone qui se trouve entre les bornes inférieure et supérieure. Les modifications apportées aux valeurs lowBound et upBound sont automatiquement appliquées à la distribution.
Cette distribution permet de déterminer la probabilité qu’une variable prenne une valeur dans une population suivant une loi du c2.
F DdP (F DdP())
Calcule la densité de probabilité (DdP) de la loi de Fisher F à une valeur x spécifiée. Le numérateur df (degrés de liberté) et le dénominateur df doivent être des entiers > 0. La fonction de densité de probabilité (DdP) est :
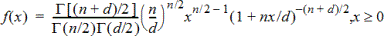
|
où |
n = degrés de liberté du numérateur |
Cette distribution permet de déterminer la probabilité selon laquelle deux échantillons ont la même variance. L’option de dessin est disponible lorsque la fonction F Pdf est invoquée depuis une cellule de formule.
F FdR (F FdR())
Calcule la fonction de répartition de la loi de Fisher F de degrés de liberté dfNumer et dfDenom entre lowBound et upBound. Vous pouvez cocher la case Dessiner (Ombrer la zone) pour ombrer la zone qui se trouve entre les bornes inférieure et supérieure. Les modifications apportées aux valeurs lowBound et upBound sont automatiquement appliquées à la distribution.
Cette distribution permet de déterminer la probabilité qu’une observation appartienne à la plage des valeurs comprises entre les bornes inférieures et supérieures.
Binomiale DdP (binomPdf())
Calcule la probabilité qu’une variable, suivant une loi binomiale discrète de paramètres n=nombre d’essais et p=probabilité de réussite, prenne la valeur x. Le paramètre x peut être un entier ou une liste d’entiers. 0{p{1 doit être vrai. nombre d’essais doit être un entier > 0. Si x n’est pas spécifié, une liste de probabilités de 0 à nombre d’essais est obtenue La fonction de densité de probabilité (DdP) est :
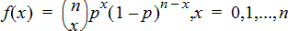
où n = nombre d’essais
Cette distribution permet de déterminer la probabilité de réussite/échec d’un essai, pour un nombre d’essais n donné. Vous pouvez par exemple utiliser cette distribution pour connaître la probabilité d’obtenir une fois « pile » au cours de cinq lancers indépendants d’une pièce
Binomiale FdR (binomCdf())
Calcule la fonction de répartition d’une loi binomiale discrète avec un nombre n d’essais et une probabilité p de réussite pour chaque essai.
Cette distribution permet de déterminer la probabilité de réussite d’un essai avant que tous les essais ne soient effectués. Par exemple, si « pile » est un lancer réussi et si vous prévoyez de lancer la pièce 10 fois, cette distribution pourra prédire le pourcentage de chance d’obtenir au moins un « pile » sur 10 lancers.
Binomiale Inverse (invBinom())
Étant donné le nombre d’essais (NumTrials) et la probabilité de réussite de chaque essai (Prob), cette fonction renvoie le nombre minimal de réussites, k, tel que la probabilité cumulée de k réussites soit supérieure ou égale à une probabilité cumulée donnée (CumulativeProb).
Binomiale Inverse en fonction de N (invBinomN())
Étant donné la probabilité de réussite de chaque essai (Prob) et le nombre de réussites (NumSuccess), cette fonction renvoie le nombre minimal d’essais, N, tel que la probabilité cumulée de x réussites soit inférieure ou égale à une probabilité cumulée donnée (CumulativeProb).
Poisson DdP (poissPdf())
Poisson DdP calcule la valeur en x de la densité de probabilité de la loi de Poisson de moyenne (µ), µ réel > 0. x peut être un entier ou une liste d’entiers. La fonction de densité de probabilité (DdP) est :
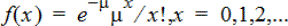
Cette distribution permet de déterminer la probabilité d’obtenir un certain nombre de réussites avant de démarrer des essais. Vous pouvez par exemple utiliser ce calcul pour anticiper le nombre de « piles » que vous obtiendrez sur huit lancers de pièce.
Poisson FdR (poissCdf())
Calcule la fonction de répartition d’une loi de Poisson discrète avec une moyenne x spécifiée.
Cette distribution permet de déterminer la probabilité selon laquelle un certain nombre de réussites sera obtenu entre deux bornes inférieure et supérieure d’essais. Vous pouvez par exemple utiliser ce calcul pour anticiper le nombre de « piles » que vous obtiendrez entre les lancers 3 et 8
Géométrique DdP (geomPdf())
Calcule la probabilité que le premier succès intervienne au rang x, pour la loi géométrique discrète en fonction de la probabilité de réussite p spécifiée. 0{p{1 doit être vrai. x peut être un entier ou une liste d’entiers. La densité de probabilité (DdP) est :
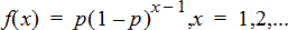
Cette distribution permet de déterminer le nombre d’essais le plus probable à effectuer avant d’obtenir une réussite. Vous pouvez par exemple utiliser ce calcul pour anticiper le nombre de lancers de pièce nécessaires avant d’obtenir un « pile ».
Géométrique FdR (geomCdf())
Calcule la fonction de répartition de la loi géométrique entre lowBound et upBound en fonction de la probabilité de réussite p spécifiée.
Cette distribution permet de déterminer la probabilité associée à la première réussite obtenue au cours des essais de 1 à n. Vous pouvez par exemple utiliser ce calcul pour déterminer la probabilité que « pile » sera obtenu au lancer Nº 1, 2, 3, ..., Nºn.