Middle grades/Algebra I
Question 1 - The Kick
Download FilesBuild reasoning skills by visualizing the flight of a field goal, observing relationships of time, distance and elevation, and discussing why the kick was good … or fell short.
You’ll need the program files, student activity pages, pre-assignment documents, and teacher notes and solutions to get started on the middle grades/algebra I activity.
Step 1
Four seconds left in the Big Game and the score is 27 to 28 - you’re behind. A 50-yard field goal wins the game. Your task is to use a mathematical model to demonstrate kicking a field goal to win the game.
Step 2
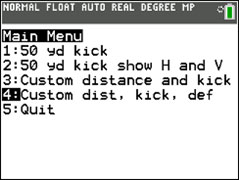
Turn on your TI-84 Plus, press [PRGM] and run the program THEKICK.
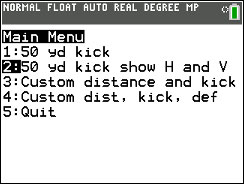
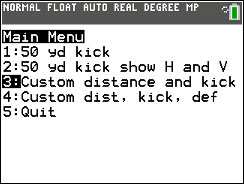
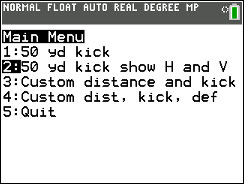
Follow the on-screen prompts to the main menu.
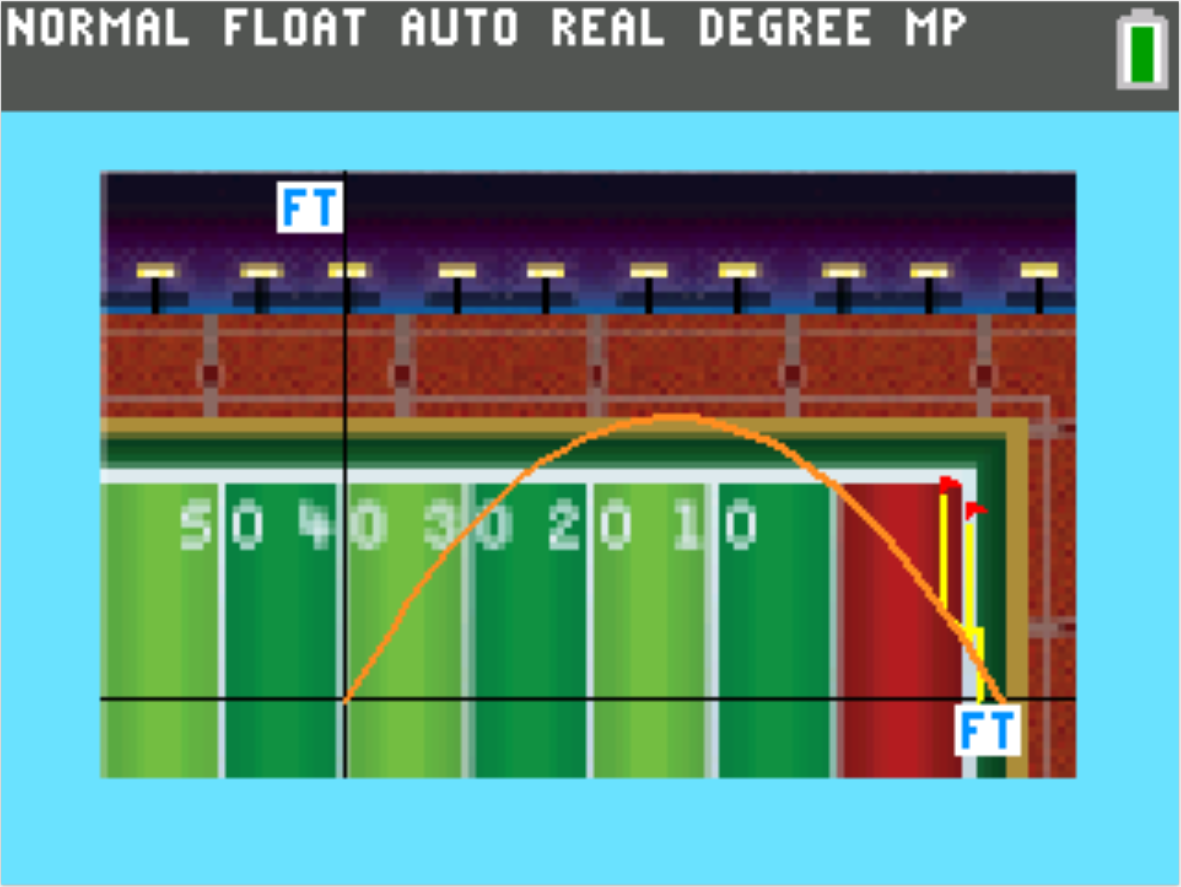
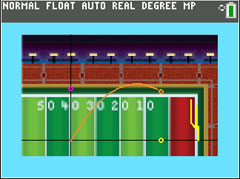
Press 1 to see the 50-yard kick.

Step 3
a. Is the field goal good? Write your guess here. (Note: To see the flight of the ball again press [2nd] [MODE] (quit) and press [ENTER] to run the program again.)
Step 4
b. Discuss with your group: When kicking a football, what things affect how far the ball travels downfield and how high the ball reaches?
Step 5
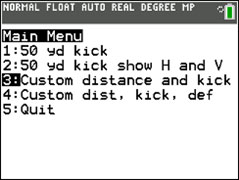
c. Press [2nd] [mode] (quit). Then run the program again but this time select Option 3 (Custom distance and kick). Use:
| Length of kick (Yards): | 50 | press [ENTER] | ||
| Angle of kick (DEG): | 35 | press [ENTER] | ||
| Velocity of kick (FT/S) | 70 | press [ENTER] |
What do you notice about the kick?
Step 6
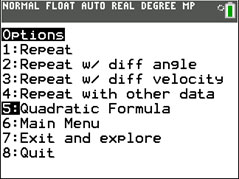
d. Professional kickers kick the football with a velocity between 70 and 88 feet per second (between 48 and 60 mph). The angle varies between 27 and 43 degrees. Press [ENTER] to view the Options menu. Using values in these ranges, take two minutes and explore several kicks using options 2, 3, and 4.
Step 7
e. Press [ENTER] to return to the Options menu. Press 6 (Main Menu). Then Option 1. Press [TRACE]. Look at the information on the screen. Notice the three variables, T, X, and Y. Press the right arrow three times and record the values to the nearest hundredth.
Step 8
f. Discuss what the values of these variables mean in this problem with your group. Include units in your discussions.
Step 9
g. Trace on the graph to where T is three-quarters of a second. (Note: just type 0.75 and press [ENTER]). Discuss what these values mean with your group; include units in your discussion.
Step 10
h. Press [2nd] [MODE] (quit) and press [ENTER] to run the program again but this time select Option 2. (Note: To see this graph again, press [ENTER] then choose Option 1, Repeat). Discuss in your groups what the yellow, pink, and orange circles represent.
Step 11
i. Press [ENTER] to return to the Options menu. Press 6 (Main Menu). Press Option 1. Press [TRACE] and graphically investigate the time when the ball is 150 feet from where it was kicked in the horizontal direction. Between what two values of T is the ball 150 feet downfield? Record the times to the nearest tenth of a second and the corresponding distances to the nearest hundredth of a foot.
Question 2 - Modeling horizontal and vertical motion
Download FilesIn order to answer Question 1i. (When is the ball 150 ft from where it was kicked?) with more precision, we need an expression to model the horizontal distance the ball travels downfield after it is kicked. Call it x(t) (read “x of t”). We also need an expression to model the vertical distance (height) of the ball after it is kicked. Call it y(t) (read “y of t”).
Both of these expressions involve ratios that are usually studied in geometry: sine and cosine. You may have been introduced to them in a pre-assignment.
Step 1
For our kick, the football was kicked at an angle of 43° with a velocity of 72 ft/s.
The function for horizontal distance traveled downfield is:
x(t) = 72 · cos(43°) · t
The function for vertical distance (height):
y(t) = 72 · sin(43°) · t - 16 · t²
Step 2
a. Algebraically calculate how long it will take for the ball to travel 150 feet downfield. Store your answer in H.
Step 3
b. Press [TRACE] and trace to this value for H and explain what the numbers on the screen mean. Is the field goal good? Explain how you know.
Question 3 - Application of the model
Download FilesRun the program THEKICK again and select Option 3. You’re going to kick a field goal to win the game. Professional kickers kick the ball with a velocity of about 70 to 88 fps (48 to 60 mph) and at an angle that varies between 27 and 43 degrees. Choose your velocity and kick angle and run the program to graph your kick.
| Length of kick (yards): | 50 | Angle (degrees): | ||
| Velocity (ft/s): |
Step 1
a. Use the equations from Question 2 that model the horizontal and vertical positions of the ball to model the actual flight of the ball after it is kicked. Write the equations for your kick below.
Step 2
b. Based on the table and graph, can you tell if the ball passes above the 10 foot crossbar on the goal posts? How can you tell?
Step 3
c. Solve algebraically for when the ball is 50 yards downfield. Use your solution to decide if the field goal is made or not. Explain your response.
Step 4
d. Attempt a 45-yard kick with a different angle or velocity and determine graphically if the kick is made using the program. Then use algebra to confirm your answer.
Extensions
Download FilesBut what about the defense?
Run the program THEKICK again and select Option 4. You’re going to kick a 50-yard field goal to win the game. Professional kickers kick the ball with a velocity of about 70 to 88 fps (48 to 60 mph) and at an angle that varies between 27 and 43 degrees. Choose your velocity and kick angle and run the program to graph your kick. The kicker kicks from 7 yards behind the line of scrimmage and the defense typically gets little or no rush (between 0 and 2 yards) and can reach about 8 to 9 feet in the air.
| Angle: | Velocity: | |||
| Rush: | Reach: |

Step 1
a. Based on your model, will a defender block the kick?
Defend your answer graphically and algebraically.
Step 2
b. Based on your model, will the ball pass above the 10-foot crossbar on the goal posts? How can you tell? Defend your answer more than one way.
Step 3
c. Attempt the kick with a different angle or velocity and determine algebraically if the kick makes it over the defense and is good. Then use the program to confirm your answer.
| Angle | Velocity | |||
| Rush | Reach | |||
| Blocked (Y/N) | Made(Y/N) |
Step 4
More Extensions
Graphically and algebraically find:
- When the ball hits the ground
- How far the ball travels horizontally
- The maximum height of the ball
Run the program and select Option 1 (1: 50-yard kick).
Step 5
a. [TRACE] to discover when the ball hits the ground and how far away the ball is from where it was kicked. Write your answers below.
Step 6
b. Algebraically find when the ball hits the ground and use that value to find how far the ball is downfield when it hits the ground. Include units in your answers and do not round the answers.
Step 7
c. Trace to discover when the ball attains its maximum height and what is the maximum height?
- Question 1
- Question 2
- Question 3
- Extensions
Geometry
Question 1 - The Kick
Download FilesBuild problem-solving abilities by manipulating variables in linear and quadratic equations to get the field goal up and over the crossbar.
You’ll need the program files, student activity pages, pre-assignment documents, and teacher notes and solutions to get started on the geometry activity.

Step 1
Four seconds left in the Big Game and the score is 27 to 28 - you're behind. A 50-yard field goal wins the game. Your task is to use a mathematical model to demonstrate kicking a field goal to win the game.
Press [PRGM] and run the program THEKICK.
Step 2
Follow the on-screen prompts to the main menu. Press 1 to see the 50-yard kick. Then press [TRACE].
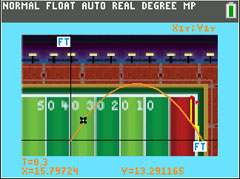
Step 3
a. Investigate the information on the screen. Notice the three variables, T, X, and Y. Press the right arrow three times and record the values of the variables to the nearest thousandth.
Step 4
b. Interpret the values of these variables in context, including units.
Step 5
c. Trace on the function to a different point and stop. Record T, X, and Y, then discuss what these values mean with your group.
Step 6
d. Using the trace feature, graphically investigate the time when the ball is 150 feet from where it was kicked in the horizontal direction. Between which two values of T does the ball pass 150 feet downfield? Record your answers to the nearest tenth of a second. How high is the ball at each of these times?
Step 7
e. Using the trace feature, graphically investigate a time when the ball is 10 feet high. Between which two values of T does the ball reach 10 feet high? Record your answers to the nearest tenth of a second. How far downfield is the ball at each of these times?
Step 8
f. Does it appear that you made the field goal? How can you tell? Can you prove you made the field goal graphically? Justify your response.
Question 2 - Modeling Horizontal Motion
Download FilesIn order to answer Question 1f. algebraically instead of on the graph, we need a function to model the horizontal distance the ball travels downfield after it’s kicked as a function of time, x(t).
Run the program THEKICK.
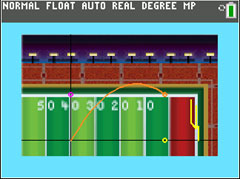
On the main menu press 2 to see a kick with the horizontal and vertical components shown. The angle of the kick is 43 degrees and the velocity of the kick is 72 ft/s. Press [ENTER] and watch the kick. You will be placed into trace mode. Press [ENTER] when you are done exploring.
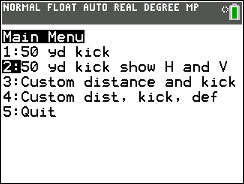
Step 1
a. Repeat the kick and watch the horizontal component (yellow). Does its speed increase, decrease, or remain constant? What does that tell you about the kind of equation that will model the horizontal motion?
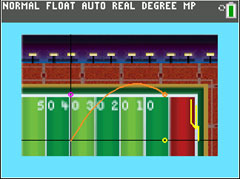
Step 2
b. The function, for the horizontal distance traveled downfield, if the ball is kicked with initial velocity 72 ft/s and an angle of 43 degrees is x(t) = 72 · cos(43°) · t. Is x(t) linear or nonlinear?
Step 3
c. How long will it take for the ball to travel 150 feet? Exit the program, then solve x(t) = 150 and store your answer in variable F.
Step 4
d. Press [TRACE]. Using the trace feature, trace to the value for F and explain what the numbers on the screen mean.
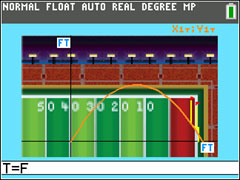
Step 5
e. Did you make the kick and win the game? How do you know?
Question 3 - Modeling Vertical Motion
Download FilesA second way to answer Question 1f. algebraically instead of graphically, uses a function to model the height of the ball during a kick as a function of time, y(t).
Run the program THEKICK.
On the main menu press 2 to see a kick with the horizontal and vertical components shown. The angle of the kick is 43 degrees and the velocity of the kick is 72 ft/s. Press [ENTER] and watch the kick. You will be placed into trace mode. Press [ENTER] when you are done exploring.
Step 1
a. Repeat the kick (Option 1 in the submenu) and this time, pay attention to the vertical component (light pink). Describe its motion. Include its speed and direction in your description. Does its speed increase, decrease, remain constant? What does that tell you about the kind of equation that will model the vertical component?
Step 2
b. What other factors besides the kick contribute to the vertical position of the ball after it’s kicked?
Step 3
Acceleration due to gravity is -32 ft/s². The negative is because the ball is being pulled down toward the ground. When modeling vertical position, we can apply physics laws to know we can add the initial velocity multiplied by the time (this gives how high the ball would be if there were no gravity) and -(1/2)g · t². The function for modeling the ball’s height, y(t), if it is kicked with an initial velocity of
72 ft/s at an angle of 43 degrees is:
y(t) = 72 · sin(43°) · t - 16 · t².
Step 4
c. What kind equation is y(t)? Is it linear or nonlinear?
Step 5
d. Solve for y(t) = 10 to determine when the ball is 10 feet in the air. (Hint: You may want to use the quadratic formula option in the program. It is Option 5 in the submenu after you’ve drawn the graph.) Use the trace feature to confirm your solution.
Step 6
e. Explain how your solution is consistent to your answer from 2e.
Extensions
Download FilesRun the program THEKICK again and select Option 3. You’re going to kick a field goal to win the game. Professional kickers kick the ball with a velocity of about 70 to 88 ft/s (48 to 60 mph) and at an angle that varies between 27 and 43 degrees. Choose your velocity and kick angle and run the program to graph your kick.
| Length of kick (yards): | Angle (degrees): | |||
| Velocity (ft/s): |
The equations you used in Questions 2 and 3 to model the horizontal and vertical positions of the ball can be used at the same time to model the actual flight of the ball after it is kicked.
Step 1
a. Based on the graph, can you tell if the ball passes above the 10-foot crossbar on the goal posts? How can you tell?
Step 2
b. Fill in the equation for x(t) and solve algebraically for when the ball passes through the goal posts. Use your solution to decide if the field goal is made or not.
x(t) = _____ cos(_____) · t
Step 3
c. Attempt the kick with a different angle or velocity and determine graphically if the kick is made using the program. Then use algebra to confirm your answer.
Angle _____ Velocity _____ Made (Y/N) _____
Step 4
But what about the defense?
Run the program Field Goal again and select Option 4. You’re going to kick a field goal to win the game. Professional kickers kick the ball with a velocity of about 70 to 88 fps (48 to 60 mph) and at an angle that varies between 27 and 43 degrees. Choose your velocity and kick angle and run the program to graph your kick. The kicker kicks from 7 yards behind the line of scrimmage and the defense typically gets little or no rush (between 0 and 2 yards) and can reach about 8 to 9 feet in the air.
Length: _______
Angle: _______
Velocity: _______
Rush: _______
Reach: _______
Step 5
a. Based on your model, will a defender block the kick? Defend your answer graphically and algebraically.
Step 6
b. Based on your model, will the ball pass above the 10-foot crossbar on the goal posts? How can you tell? Defend your answer more than one way.
Step 7
c. Attempt the kick with a different angle or velocity and determine algebraically if the kick makes it over the defense and is good. Then use the program to confirm your answer.
Angle ______ Velocity _______
Rush _______ Reach ______
Blocked (Y/N) _______ Made (Y/N) _______
- Question 1
- Question 2
- Question 3
- Extensions
Algebra II
Question 1 - The Kick
Download FilesDevelop equations and graphs to analyze the success (or failure) of your season’s final play.
You’ll need the program files, student activity pages, pre-assignment documents, and teacher notes and solutions to get started on the algebra II activity.

Step 1
Four seconds left in the Big Game and the score is 27 to 28 - you’re behind. A 50-yard field goal wins the game. Your task is to create a mathematical model to demonstrate kicking a field goal to win the game.
Press [PRGM] and run the program THEKICK.
Step 2
Follow the on-screen prompts to the main menu.
Press 1 to see the 50-yard kick. Then press [TRACE].
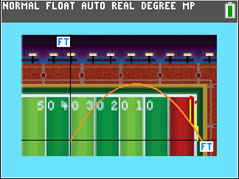
Step 3
a. Investigate the information on the screen. Notice the three variables, T, X, and Y. Press the right arrow three times and record the values of the variables to the nearest thousandth.
T = __________
X = __________
Y = __________
Step 4
b. Interpret the values of these variables in context, including units.
Step 5
c. Trace on the function to a different point and stop. Record T, X, and Y, then discuss what these values mean with your group.
Step 6
d. Using the trace feature, graphically investigate the time when the ball is 150 feet from where it was kicked in the horizontal direction. Between which two values of T does the ball pass 150 feet downfield? Record your answers to the nearest tenth of a second. How high is the ball at each of these times?
Step 7
e. Does it appear that you made the field goal? How can you tell? Can you prove you made the field goal graphically? Justify your response.
Question 2 - Modeling Horizontal Motion
Download FilesIn order to answer Question 1e. algebraically instead of on the graph, we need a function to model the horizontal distance the ball travels downfield after it’s kicked as a function of time, x(t).
When the ball is kicked at a given angle, θ, with a given velocity, the velocity has a horizontal component, and a vertical component.
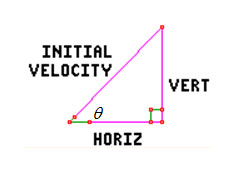
Step 1
Run the program THEKICK.
On the main menu press 2 to see a kick with the horizontal and vertical components shown. The angle of the kick is 43 degrees and the velocity of the kick is 72 ft/s. Press [ENTER] and watch the kick. You will be placed into trace mode. Press [ENTER] when you are done exploring.
Step 2
a. If the velocity of the kick is 72 ft/s at an angle of 43°, complete the triangle below.
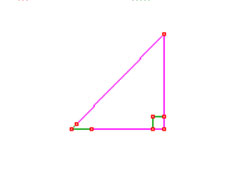

Step 3
b. Repeat the kick and watch the horizontal component (yellow). Does its speed increase, decrease, or remain constant? What does that tell you about the kind of equation that will model the horizontal motion?
Step 4
c. Write a function, x(t) for the horizontal distance traveled downfield, if the ball is kicked with initial velocity 72 ft/s and an angle of 43 degrees. (Hint: recall your trigonometric ratios and the fact that distance = rate · time )
Step 5
d. How long will it take for the ball to travel 150 feet? Exit the program, then solve x(t) = 150 and store your answer in variable F.
Step 6
e. Press [TRACE]. Using the trace feature, trace to the value for F and explain what the numbers on the screen mean.
Step 7
f. Did you make the kick and win the game? How do you know?
Question 3 - Modeling Vertical Motion
Download FilesA second way to answer question 1f. algebraically instead of graphically, uses a function to model the height of the ball during a kick as a function of time, y(t).
Step 1
Run the program THEKICK.
On the main menu press 2 to see a kick with the horizontal and vertical components shown. The angle of the kick is 43 degrees and the velocity of the kick is 72 ft/s. Press [ENTER] and watch the kick. You will be placed into trace mode. Press [ENTER] when you are done exploring.
Step 2
a. If the velocity of the kick is 72 ft/s at an angle of 43°, complete the triangle below.


Step 3
b. Repeat the kick and this time, pay attention to the vertical component (light pink). Describe its motion. Include its speed and direction in your description. Does its speed increase, decrease, remain constant? What does that tell you about the kind of equation that will model the vertical position of the ball as a function of time?

Step 4
c. What other factors besides the kick contribute to the vertical position of the ball after it’s kicked?
Step 5
d. Acceleration due to gravity is -32 ft/s². The negative is because the ball is being pulled down toward the ground. When modeling vertical position, we can apply physics laws to know we can add the vertical component of the kick multiplied by the time (this gives how high the ball would be if there were no gravity) and -(1/2)g · t². Write the function for modeling the ball’s vertical position, y(t), if it is kicked with an initial velocity of 72 ft/s at an angle of 43°.
Step 6
e. Solve for y(t) = 10 to determine when the ball is 10 feet in the air. (Hint: you may want to use the quadratic formula option in the program. It is Option 5 in the submenu after you’ve drawn the graph.) Use the trace feature to confirm your solution.
Step 7
f. Explain how your solution is consistent to your answer from 2f.
Extensions
Download FilesApplication of the model
Run the program THEKICK again and select Option 3. You’re going to kick field goal to win the game. Professional kickers kick the ball with a velocity of about 72 to 88 ft/s (49 to 60 mph) and at an angle that varies between 27 and 43 degrees. Choose your velocity and kick angle and run the program to graph your kick.
| Length of kick (yards): | Angle (degrees): | |||
| Velocity (ft/s): |

Step 1
a. Based on the table and graph can you tell if the ball passes above the 10-foot crossbar on the goal posts? How can you tell?
Step 2
b. Fill in the equation for x(t) and solve algebraically for when the ball passes through the goal posts. Use your solution to decide if the field goal is made or not.
x(t) = _______ cos(_____)·t
Step 3
c. Attempt the kick with a different angle or velocity and determine graphically if the kick is made using the program. Then use algebra to confirm your answer.
Angle _____ Velocity _____ Made (Y/N) _____
Step 4
But what about the defense?
Run the program THEKICK again and select Option 4. You’re going to kick a 50-yard field goal to win the game. Professional kickers kick the ball with a velocity of about 70 to 88 ft/s (48 to 60 mph) and at an angle that varies between 27 and 43 degrees. Choose your velocity and kick angle and run the program to graph your kick. The kicker kicks from 7 yards behind the line of scrimmage and the defense typically gets little or no rush (between 0 and 1 yards) and can reach about 8 to 9 feet in the air.
Length: _______
Angle: _______
Velocity: _______
Rush: _______
Reach: _______

Step 5
a. Based on your model, will a defender block the kick? Defend your answer graphically and algebraically.
Step 6
b. Based on your model, will the ball pass above the 10-foot crossbar on the goal posts? How can you tell? Defend your answer more than one way.
Step 7
c. Attempt the kick with a different angle or velocity and determine algebraically if the kick makes it over the defense and is good. Then use the program to confirm your answer.
Angle ______ Velocity _______
Rush _______ Reach ______
Blocked (Y/N) _______ Made (Y/N) _______
- Question 1
- Question 2
- Question 3
- Extensions
Porta Ultricies Cras
Sign up for updates