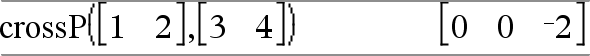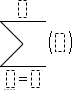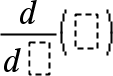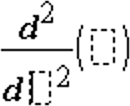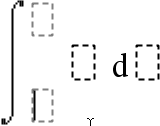Expression Templates

Expression templates give you an easy way to enter math expressions in standard mathematical notation. When you insert a template, it appears on the entry line with small blocks at positions where you can enter elements. A cursor shows which element you can enter.

Position the cursor on each element, and type a value or expression for the element.

Fraction template

/p keys

Note: See also / (divide), here.

Example:

Exponent template

l key

Note: Type the first value, press l, and then type the exponent. To return the cursor to the baseline, press right arrow (¢).

Note: See also ^ (power), here.

Example:

Square root template

/q keys

Note: See also √() (square root), here.

Example:

Nth root template

/l keys

Note: See also root(), here.

Example:

e exponent template

u keys

Natural exponential e raised to a power

Note: See also e^(), here.

Example:

Log template

/s key

Calculates log to a specified base. For a default of base 10, omit the base.

Note: See also log(), here.

Example:

Piecewise template (2-piece)

Catalog >

Lets you create expressions and conditions for a two‑piece piecewise function. To add a piece, click in the template and repeat the template.

Note: See also piecewise(), here.

Example:

Piecewise template (N-piece)

Catalog >

Lets you create expressions and conditions for an N‑piece piecewise function. Prompts for N.

Note: See also piecewise(), here.

Example:

See the example for Piecewise template (2-piece).

System of 2 equations template

Catalog >

Creates a system of two linear equations. To add a row to an existing system, click in the template and repeat the template.

Note: See also system(), here.

Example:

System of N equations template

Catalog >

Lets you create a system of N linear equations. Prompts for N.

Note: See also system(), here.

Example:

See the example for System of equations template (2-equation).

Absolute value template

Catalog >

Note: See also abs(), here.

Example:

dd°mm’ss.ss’’ template

Catalog >

 

Lets you enter angles in dd°mm’ss.ss’’ format, where dd is the number of decimal degrees, mm is the number of minutes, and ss.ss is the number of seconds.

Example:

Matrix template (2 x 2)

Catalog >

Creates a 2 x 2 matrix.

Example:

Matrix template (1 x 2)

Catalog >

.

Example:

Matrix template (2 x 1)

Catalog >

Example:

Matrix template (m x n)

Catalog >

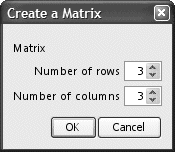
The template appears after you are prompted to specify the number of rows and columns.

Note: If you create a matrix with a large number of rows and columns, it may take a few moments to appear.

Example:

Sum template (Σ)

Catalog >

Note: See also Σ() (sumSeq), here.

Example:

Product template (Π)

Catalog >

Note: See also Π() (prodSeq), here.

Example:

First derivative template

Catalog >

The first derivative template can be used to calculate first derivative at a point numerically, using auto differentiation methods.

Note: See also d() (derivative), here.

Example:

Second derivative template

Catalog >

The second derivative template can be used to calculate second derivative at a point numerically, using auto differentiation methods.

Note: See also d() (derivative), here.

Example:

Definite integral template

Catalog >

The definite integral template can be used to calculate the definite integral numerically, using the same method as nInt().

Note: See also nInt(), here.

Example:
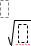
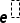
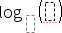
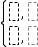
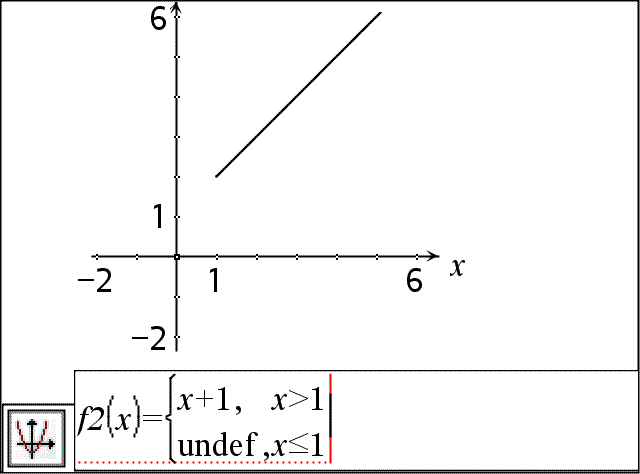
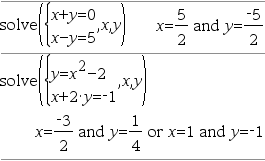