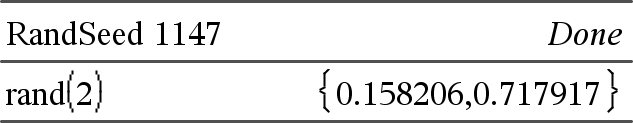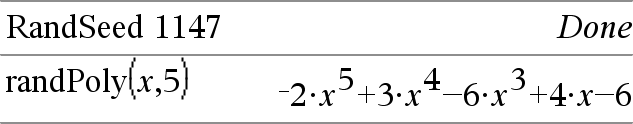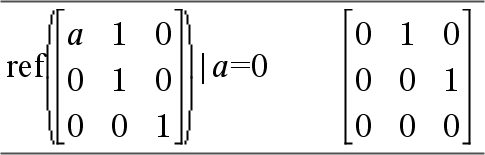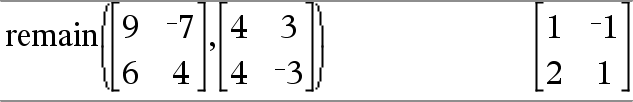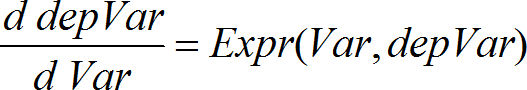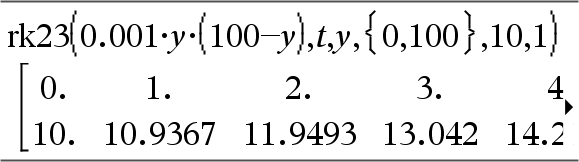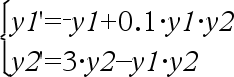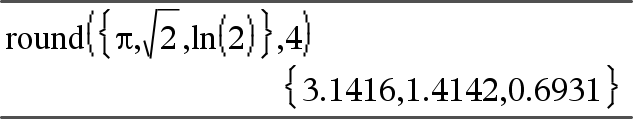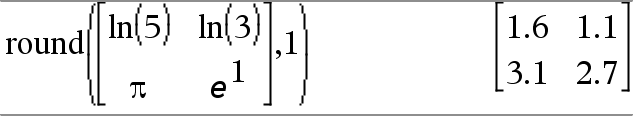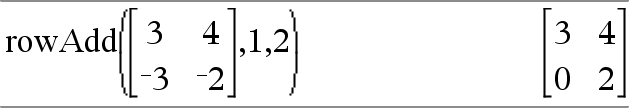R

R►Pθ()

Catalog >


R►Pθ (xValue, yValue) ⇒ value
R►Pθ (xList, yList) ⇒ list
R►Pθ (xMatrix, yMatrix) ⇒ matrix

Returns the equivalent θ-coordinate of the
(x,y) pair arguments.

Note: The result is returned as a degree, gradian or radian angle, according to the current angle mode setting.

Note: You can insert this function from the computer keyboard by typing R@>Ptheta(...).

In Degree angle mode:


In Gradian angle mode:


In Radian angle mode:

R►Pr()

Catalog >


R►Pr (xValue, yValue) ⇒ value
R►Pr (xList, yList) ⇒ list
R►Pr (xMatrix, yMatrix) ⇒ matrix

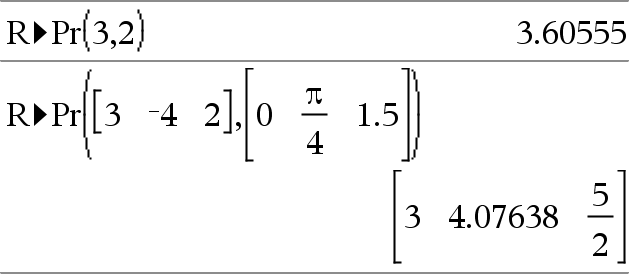
Returns the equivalent r-coordinate of the (x,y) pair arguments.

Note: You can insert this function from the computer keyboard by typing R@>Pr(...).

In Radian angle mode:

►Rad

Catalog >

Value1►Rad ⇒ value

Converts the argument to radian angle measure.

Note: You can insert this operator from the computer keyboard by typing @>Rad.

In Degree angle mode:


In Gradian angle mode:

rand()

Catalog >

rand() ⇒ expression
rand(#Trials) ⇒ list

rand() returns a random value between 0 and 1.

rand(#Trials) returns a list containing #Trials random values between 0 and 1.

Set the random-number seed.

randBin()

Catalog >

randBin(n, p) ⇒ expression
randBin(n, p, #Trials) ⇒ list

randBin(n, p) returns a random real number from a specified Binomial distribution.

randBin(n, p, #Trials) returns a list containing #Trials random real numbers from a specified Binomial distribution.

randInt()

Catalog >

randInt(lowBound,upBound) ⇒ expression
randInt(lowBound,upBound ,#Trials) ⇒ list

randInt(lowBound,upBound) returns a random integer within the range specified by lowBound and upBound integer bounds.

randInt(lowBound,upBound ,#Trials) returns a list containing #Trials random integers within the specified range.

randMat()

Catalog >

randMat(numRows, numColumns) ⇒ matrix

Returns a matrix of integers between -9 and 9 of the specified dimension.

Both arguments must simplify to integers.

Note: The values in this matrix will change each time you press ·.

randNorm()

Catalog >

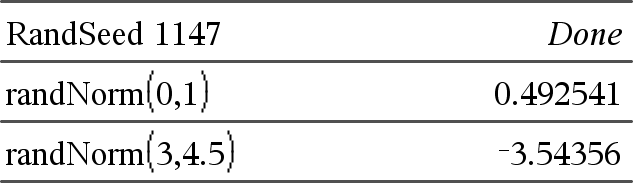
randNorm(μ, σ) ⇒ expression
randNorm(μ, σ, #Trials) ⇒ list

randNorm(μ, σ) returns a decimal number from the specified normal distribution. It could be any real number but will be heavily concentrated in the interval [μ−3•σ, μ+3•σ].

randNorm(μ, σ, #Trials) returns a list containing #Trials decimal numbers from the specified normal distribution.

randPoly()

Catalog >

randPoly(Var, Order) ⇒ expression

Returns a polynomial in Var of the specified Order. The coefficients are random integers in the range −9 through 9. The leading coefficient will not be zero.

Order must be 0–99.

randSamp()

Catalog >

randSamp(List,#Trials[,noRepl]) ⇒ list

Returns a list containing a random sample of #Trials trials from List with an option for sample replacement (noRepl=0), or no sample replacement (noRepl=1). The default is with sample replacement.

RandSeed

Catalog >

RandSeed Number

If Number = 0, sets the seeds to the factory defaults for the random-number generator. If Number ≠ 0, it is used to generate two seeds, which are stored in system variables seed1 and seed2.

real()

Catalog >

real(Value1) ⇒ value

Returns the real part of the argument.

real(List1) ⇒ list

Returns the real parts of all elements.

real(Matrix1) ⇒ matrix

Returns the real parts of all elements.

►Rect

Catalog >

Vector ►Rect

Note: You can insert this operator from the computer keyboard by typing @>Rect.

Displays Vector in rectangular form [x, y, z]. The vector must be of dimension 2 or 3 and can be a row or a column.

Note: ►Rect is a display-format instruction, not a conversion function. You can use it only at the end of an entry line, and it does not update ans.

Note: See also ►Polar, here.

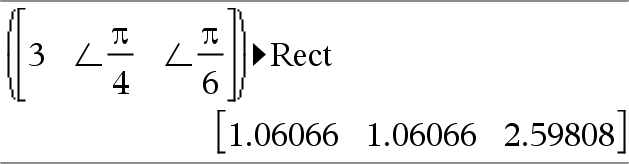
complexValue ►Rect

Displays complexValue in rectangular form a+bi. The complexValue can have any complex form. However, an reiθ entry causes an error in Degree angle mode.

Note: You must use parentheses for an (r∠θ) polar entry.

In Radian angle mode:


In Gradian angle mode:


In Degree angle mode:

Note: To type ∠, select it from the symbol list in the Catalog.

ref()

Catalog >

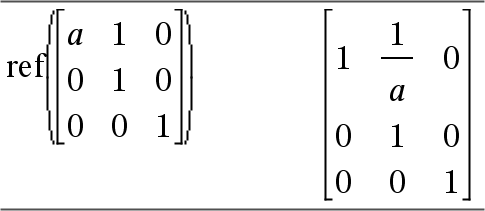
ref(Matrix1[, Tol]) ⇒ matrix

Returns the row echelon form of Matrix1.

Optionally, any matrix element is treated as zero if its absolute value is less than Tol. This tolerance is used only if the matrix has floating-point entries and does not contain any symbolic variables that have not been assigned a value. Otherwise, Tol is ignored.

• If you use /· or set the Auto or Approximate mode to Approximate, computations are done using floating-point arithmetic.
• If Tol is omitted or not used, the default tolerance is calculated as:
5E−14 •max(dim(Matrix1)) •rowNorm(Matrix1)

Avoid undefined elements in Matrix1. They can lead to unexpected results.

For example, if a is undefined in the following expression, a warning message appears and the result is shown as:

The warning appears because the generalized element 1/a would not be valid for a=0.

You can avoid this by storing a value to a beforehand or by using the constraint (“|”) operator to substitute a value, as shown in the following example.

Note: See also rref(), here.

 

RefreshProbeVars

Catalog >

RefreshProbeVars

Allows you to access sensor data from all connected sensor probes in your TI-Basic program.

StatusVar Value

Status

statusVar=0

Normal (continue with the program)

statusVar=1

The Vernier DataQuest™ application is in data collection mode.

Note: The Vernier DataQuest™ application must be in meter mode for this command to work.

statusVar=2

The Vernier DataQuest™ application is not launched.

statusVar=3

The Vernier DataQuest™ application is launched, but you have not connected any probes.

Example

Define temp()=

Prgm

© Check if system is ready

RefreshProbeVars status

If status=0 Then

Disp "ready"

For n,1,50

RefreshProbeVars status

temperature:=meter.temperature

Disp "Temperature: ",temperature

If temperature>30 Then

Disp "Too hot"

EndIf

© Wait for 1 second between samples

Wait 1

EndFor

Else

Disp "Not ready. Try again later"

EndIf

EndPrgm

 

Note: This can also be used with TI-Innovator™ Hub.

 

remain()

Catalog >


remain(Value1, Value2) ⇒ value
remain(List1, List2) ⇒ list
remain(Matrix1, Matrix2) ⇒ matrix

Returns the remainder of the first argument with respect to the second argument as defined by the identities:

remain(x,0)   x
remain(x,y)   x−y•iPart(x/y)

As a consequence, note that remain(−x,y) − remain(x,y). The result is either zero or it has the same sign as the first argument.

Note: See also mod(), here.

Request

Catalog >

Request promptString, var[, DispFlag [, statusVar]]

Request promptString, func(arg1, ...argn)  [, DispFlag [, statusVar]]

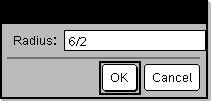
Programming command: Pauses the program and displays a dialog box containing the message promptString and an input box for the user’s response.

When the user types a response and clicks OK, the contents of the input box are assigned to variable var.

If the user clicks Cancel, the program proceeds without accepting any input. The program uses the previous value of var if var was already defined.

The optional DispFlag argument can be any expression.

• If DispFlag is omitted or evaluates to 1, the prompt message and user’s response are displayed in the Calculator history.
• If DispFlag evaluates to 0, the prompt and response are not displayed in the history.

Define a program:

Define request_demo()=Prgm
    Request “Radius: ”,r
    Disp “Area = “,pi*r2
EndPrgm

 

Run the program and type a response:

request_demo()

Result after selecting OK:

Radius: 6/2
Area= 28.2743

The optional statusVar argument gives the program a way to determine how the user dismissed the dialog box. Note that statusVar requires the DispFlag argument.

• If the user clicked OK or pressed Enter or Ctrl+Enter, variable statusVar is set to a value of 1.
• Otherwise, variable statusVar is set to a value of 0.

The func() argument allows a program to store the user’s response as a function definition. This syntax operates as if the user executed the command:

     Define func(arg1, ...argn) = user’s response

The program can then use the defined function func(). The promptString should guide the user to enter an appropriate user’s response that completes the function definition.

Note: You can use the Request command within a user-defined program but not within a function.

To stop a program that contains a Request command inside an infinite loop:

• Handheld: Hold down the c key and press · repeatedly.
• Windows®: Hold down the F12 key and press Enter repeatedly.
• Macintosh®: Hold down the F5 key and press Enter repeatedly.
• iPad®: The app displays a prompt. You can continue waiting or cancel.

Note: See also RequestStr, here.

Define a program:

Define polynomial()=Prgm
    Request "Enter a polynomial in x:",p(x)
    Disp "Real roots are:",polyRoots(p(x),x)
EndPrgm

 

Run the program and type a response:

polynomial()

Result after entering x^3+3x+1 and selecting OK:

Real roots are: {-0.322185}

RequestStr

Catalog >

RequestStr promptString, var[, DispFlag]

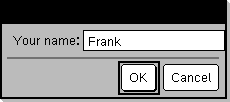
Programming command: Operates identically to the first syntax of the Request command, except that the user’s response is always interpreted as a string. By contrast, the Request command interprets the response as an expression unless the user encloses it in quotation marks (““).

Note: You can use the RequestStr command within a user-defined program but not within a function.

To stop a program that contains a RequestStr command inside an infinite loop:

• Handheld: Hold down the c key and press · repeatedly.
• Windows®: Hold down the F12 key and press Enter repeatedly.
• Macintosh®: Hold down the F5 key and press Enter repeatedly.
• iPad®: The app displays a prompt. You can continue waiting or cancel.

Note: See also Request, here.

Define a program:

Define requestStr_demo()=Prgm
    RequestStr “Your name:”,name,0
    Disp “Response has “,dim(name),” characters.”
EndPrgm

 

Run the program and type a response:

requestStr_demo()

 

Result after selecting OK (Note that the DispFlag argument of 0 omits the prompt and response from the history):

 

requestStr_demo()

Response has 5 characters.

Return

Catalog >

Return [Expr]

Returns Expr as the result of the function. Use within a Func...EndFunc block.

Note: Use Return without an argument within a Prgm...EndPrgm block to exit a program.

Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook.

right()

Catalog >

right(List1[, Num]) ⇒ list

Returns the rightmost Num elements contained in List1.

If you omit Num, returns all of List1.

right(sourceString[, Num]) ⇒ string

Returns the rightmost Num characters contained in character string sourceString.

If you omit Num, returns all of sourceString.

right(Comparison) ⇒ expression

Returns the right side of an equation or inequality.

rk23 ()

Catalog >

rk23(Expr, Var, depVar, {Var0, VarMax}, depVar0, VarStep [, diftol]) ⇒ matrix

rk23(SystemOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

rk23(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0, VarStep[, diftol]) ⇒ matrix

Uses the Runge-Kutta method to solve the system

with depVar(Var0)=depVar0 on the interval [Var0,VarMax]. Returns a matrix whose first row defines the Var output values as defined by VarStep. The second row defines the value of the first solution component at the corresponding Var values, and so on.

Expr is the right hand side that defines the ordinary differential equation (ODE).

SystemOfExpr is a system of right-hand sides that define the system of ODEs (corresponds to order of dependent variables in ListOfDepVars).

ListOfExpr is a list of right-hand sides that define the system of ODEs (corresponds to order of dependent variables in ListOfDepVars).

Var is the independent variable.

ListOfDepVars is a list of dependent variables.

{Var0, VarMax} is a two-element list that tells the function to integrate from Var0 to VarMax.

ListOfDepVars0 is a list of initial values for dependent variables.

If VarStep evaluates to a nonzero number: sign(VarStep) = sign(VarMax-Var0) and solutions are returned at Var0+i*VarStep for all i=0,1,2,… such that Var0+i*VarStep is in [var0,VarMax] (may not get a solution value at VarMax).

if VarStep evaluates to zero, solutions are returned at the "Runge-Kutta" Var values.

diftol is the error tolerance (defaults to 0.001).

Differential equation:

y'=0.001*y*(100-y) and y(0)=10

To see the entire result,
press 5 and then use 7 and 8 to move the cursor.

Same equation with diftol set to 1.E−6

System of equations:

with y1(0)=2 and y2(0)=5

root()

Catalog >

root(Value) ⇒ root
root(Value1, Value2) ⇒ root

root(Value) returns the square root of Value.

root(Value1, Value2) returns the Value2 root of Value1. Value1 can be a real or complex floating point constant or an integer or complex rational constant.

Note: See also Nth root template, here.

rotate()

Catalog >

rotate(Integer1[,#ofRotations]) ⇒ integer

Rotates the bits in a binary integer. You can enter Integer1 in any number base; it is converted automatically to a signed, 64-bit binary form. If the magnitude of Integer1 is too large for this form, a symmetric modulo operation brings it within the range. For more information, see ►Base2,  here.

In Bin base mode:

 

To see the entire result,
press 5 and then use 7 and 8 to move the cursor.

If #ofRotations is positive, the rotation is to the left. If #ofRotations is negative, the rotation is to the right. The default is −1 (rotate right one bit).

For example, in a right rotation:

In Hex base mode:

Each bit rotates right.

0b00000000000001111010110000110101

Rightmost bit rotates to leftmost.

produces:

0b10000000000000111101011000011010

The result is displayed according to the Base mode.

Important: To enter a binary or hexadecimal number, always use the 0b or 0h prefix (zero, not the letter O).

rotate(List1[,#ofRotations]) ⇒ list

Returns a copy of List1 rotated right or left by #of Rotations elements. Does not alter List1.

If #ofRotations is positive, the rotation is to the left. If #of Rotations is negative, the rotation is to the right. The default is −1 (rotate right one element).

In Dec base mode:

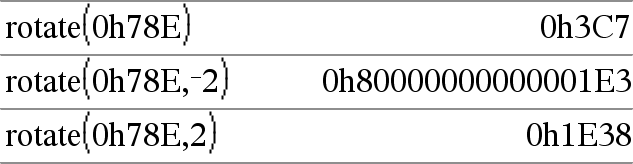
rotate(String1[,#ofRotations]) ⇒ string

Returns a copy of String1 rotated right or left by #ofRotations characters. Does not alter String1.

If #ofRotations is positive, the rotation is to the left. If #ofRotations is negative, the rotation is to the right. The default is −1 (rotate right one character).

round()

Catalog >

round(Value1[, digits]) ⇒ value

Returns the argument rounded to the specified number of digits after the decimal point.

digits must be an integer in the range 0–12. If digits is not included, returns the argument rounded to 12 significant digits.

Note: Display digits mode may affect how this is displayed.

round(List1[, digits]) ⇒ list

Returns a list of the elements rounded to the specified number of digits.

round(Matrix1[, digits]) ⇒ matrix

Returns a matrix of the elements rounded to the specified number of digits.

rowAdd()

Catalog >

rowAdd(Matrix1, rIndex1, rIndex2) ⇒ matrix

Returns a copy of Matrix1 with row rIndex2 replaced by the sum of rows rIndex1 and rIndex2.

rowDim()

Catalog >

rowDim(Matrix) ⇒ expression

Returns the number of rows in Matrix.

Note: See also colDim(), here.

rowNorm()

Catalog >

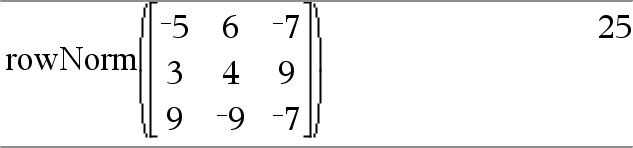
rowNorm(Matrix) ⇒ expression

Returns the maximum of the sums of the absolute values of the elements in the rows in Matrix.

Note: All matrix elements must simplify to numbers. See also colNorm(), here.

rowSwap()

Catalog >

rowSwap(Matrix1, rIndex1, rIndex2) ⇒ matrix

Returns Matrix1 with rows rIndex1 and rIndex2 exchanged.

rref()

Catalog >

rref(Matrix1[, Tol]) ⇒ matrix

Returns the reduced row echelon form of Matrix1.

Optionally, any matrix element is treated as zero if its absolute value is less than Tol. This tolerance is used only if the matrix has floating-point entries and does not contain any symbolic variables that have not been assigned a value. Otherwise, Tol is ignored.

• If you use /· or set the Auto or Approximate mode to Approximate, computations are done using floating-point arithmetic.
• If Tol is omitted or not used, the default tolerance is calculated as:
5E−14 •max(dim(Matrix1)) •rowNorm(Matrix1)

Note: See also ref(), here.