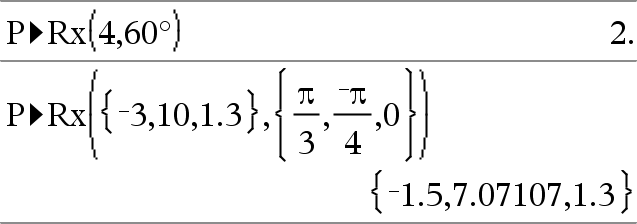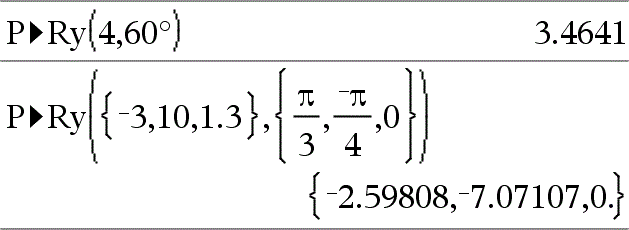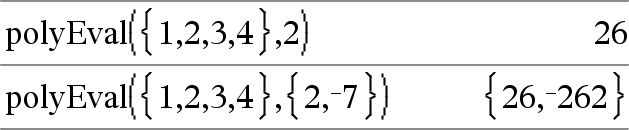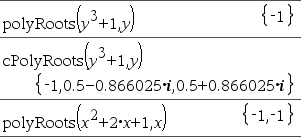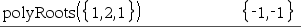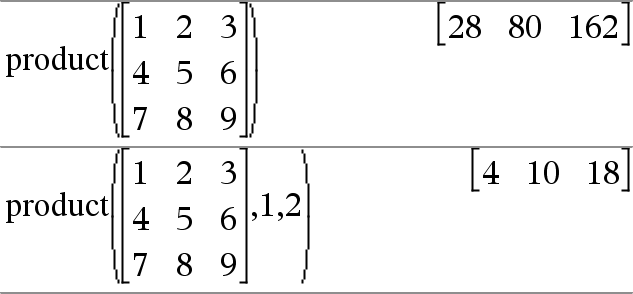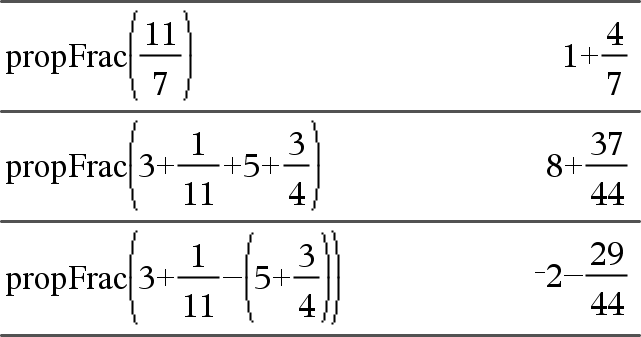P►Rx(rExpr, θExpr) ⇒ expression
P►Rx(rList, θList) ⇒ list
P►Rx(rMatrix, θMatrix) ⇒ matrix

Returns the equivalent x-coordinate of the (r, θ) pair.

Note: The θ argument is interpreted as either a degree, gradian or radian angle, according to the current angle mode. If the argument is an expression, you can use °, G, or r to override the angle mode setting temporarily.

Note: You can insert this function from the computer keyboard by typing P@>Rx(...).

P►Ry(rValue, θValue) ⇒ value
P►Ry(rList, θList) ⇒ list
P►Ry(rMatrix, θMatrix) ⇒ matrix

Returns the equivalent y-coordinate of the (r, θ) pair.

Note: The θ argument is interpreted as either a degree, radian or gradian angle, according to the current angle mode.°r

Note: You can insert this function from the computer keyboard by typing P@>Ry(...).

PassErr

Passes an error to the next level.

If system variable errCode is zero, PassErr does not do anything.

The Else clause of the Try...Else...EndTry block should use ClrErr or PassErr. If the error is to be processed or ignored, use ClrErr. If what to do with the error is not known, use PassErr to send it to the next error handler. If there are no more pending Try...Else...EndTry error handlers, the error dialog box will be displayed as normal.

Note: See also ClrErr, here, and Try, here.

Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook.

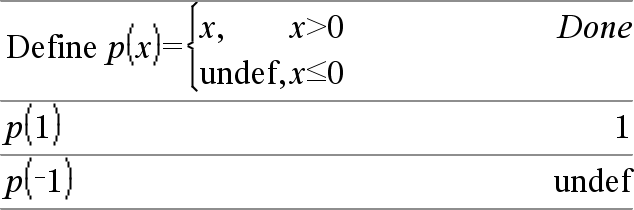
piecewise(Expr1[, Cond1[, Expr2 [, Cond2[, … ]]]])

Returns definitions for a piecewise function in the form of a list. You can also create piecewise definitions by using a template.

Note: See also Piecewise template, here.

poissCdf(λ,lowBound,upBound) ⇒ number if lowBound and upBound are numbers, list if lowBound and upBound are lists

poissCdf(λ,upBound)for P(0≤X≤upBound) ⇒ number if upBound is a number, list if upBound is a list

Computes a cumulative probability for the discrete Poisson distribution with specified mean λ.

For P(X ≤ upBound), set lowBound=0

poissPdf(λ,XVal) ⇒ number if XVal is a number, list if XVal is a list

Computes a probability for the discrete Poisson distribution with the specified mean λ.

complexValue ►Polar

Displays complexVector in polar form.

complexValue can have any complex form. However, an reiθ entry causes an error in Degree angle mode.

Note: You must use the parentheses for an (r∠θ) polar entry.

polyEval(List1, Expr1) ⇒ expression
polyEval(List1, List2) ⇒ expression

Interprets the first argument as the coefficient of a descending-degree polynomial, and returns the polynomial evaluated for the value of the second argument.

polyRoots(Poly,Var) ⇒ list

polyRoots(ListOfCoeffs) ⇒ list

The first syntax, polyRoots(Poly,Var), returns a list of real roots of polynomial Poly with respect to variable Var. If no real roots exist, returns an empty list: { }.

Poly must be a polynomial in expanded form in one variable. Do not use unexpanded forms such as y2•y+1 or x•x+2•x+1

The second syntax, polyRoots(ListOfCoeffs), returns a list of real roots for the coefficients in ListOfCoeffs.

Note: See also cPolyRoots(), here.

PowerReg X,Y[, Freq][, Category, Include]]

Computes the power regressiony = (a•(x)b)on lists X and Y with frequency Freq. A summary of results is stored in the stat.results variable. (See here.)

All the lists must have equal dimension except for Include.

X and Y are lists of independent and dependent variables.

Freq is an optional list of frequency values. Each element in Freq specifies the frequency of occurrence for each corresponding X and Y data point. The default value is 1. All elements must be integers ≥ 0.

Category is a list of numeric or string category codes for the corresponding X and Y data.

Include is a list of one or more of the category codes. Only those data items whose category code is included in this list are included in the calculation.

For information on the effect of empty elements in a list, see “Empty (Void) Elements,” here.

Prgm
     Block
EndPrgm

Template for creating a user-defined program. Must be used with the Define, Define LibPub, or Define LibPriv command.

Block can be a single statement, a series of statements separated with the “:” character, or a series of statements on separate lines.

Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook.

product(Matrix1[, Start[, End]]) ⇒ matrix

Returns a row vector containing the products of the elements in the columns of Matrix1. Start and end are optional. They specify a range of rows.

Empty (void) elements are ignored. For more information on empty elements, see here.

You can use the propFrac() function to represent mixed fractions and demonstrate addition and subtraction of mixed fractions.