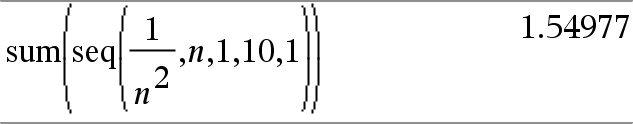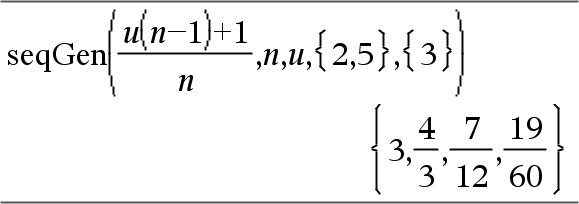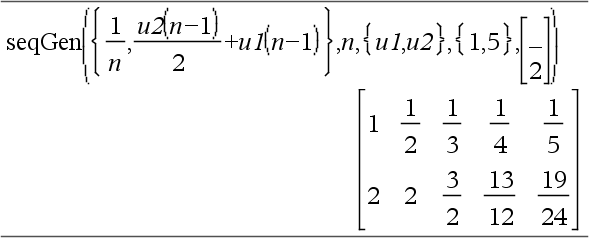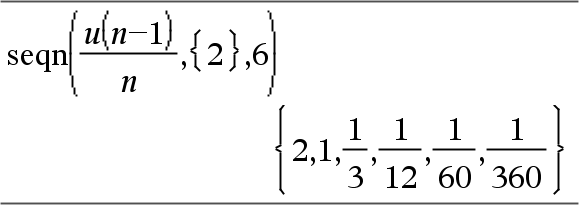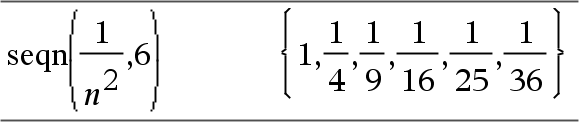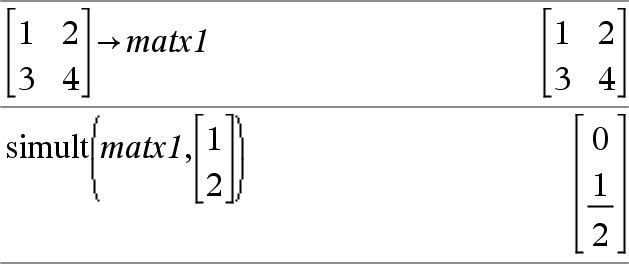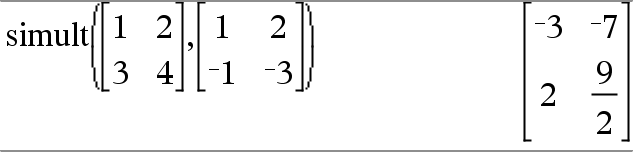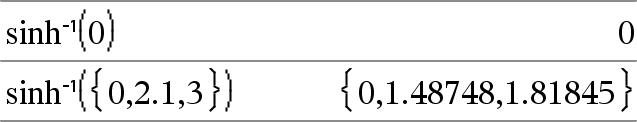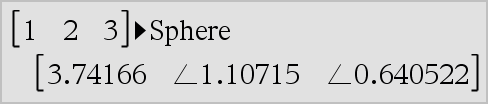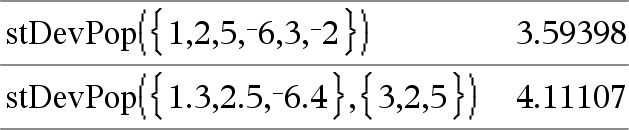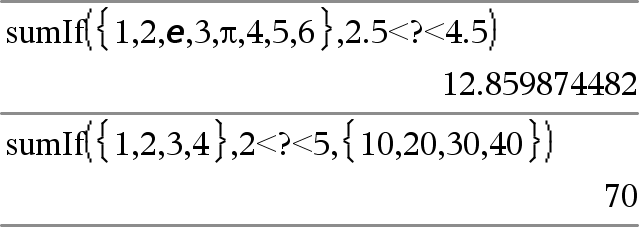|
µ key |
|
|
Returns the secant of Value1 or returns a list containing the secants of all elements in List1. Note: The argument is interpreted as a degree, gradian or radian angle, according to the current angle mode setting. You can use °, G, or r to override the angle mode temporarily. |
In Degree angle mode:
|
|
µ key |
|
|
Returns the angle whose secant is Value1 or returns a list containing the inverse secants of each element of List1. Note: The result is returned as a degree, gradian, or radian angle, according to the current angle mode setting. Note: You can insert this function from the keyboard by typing arcsec(...). |
In Degree angle mode:
|
|
Catalog > |
|
|
|
|
|
Catalog > |
|
|
Returns the inverse hyperbolic secant of Value1 or returns a list containing the inverse hyperbolic secants of each element of List1. Note: You can insert this function from the keyboard by typing arcsech(...). |
In Radian angle and Rectangular complex mode:
|
|
Hub Menu |
|
|
Programming command: Sends one or more TI-Innovator™ Hub commands to a connected hub. exprOrString must be a valid TI-Innovator™ Hub Command. Typically, exprOrString contains a "SET ..." command to control a device or a "READ ..." command to request data. The arguments are sent to the hub in succession. Note: You can use the Send command within a user-defined program but not within a function. Note: See also Get (here), GetStr (here), and eval() (here). |
Example: Turn on the blue element of the built-in RGB LED for 0.5 seconds.
Example: Request the current value of the hub's built-in light-level sensor. A Get command retrieves the value and assigns it to variable lightval.
Example: Send a calculated frequency to the hub's built-in speaker. Use special variable iostr.SendAns to show the hub command with the expression evaluated.
|
|
Catalog > |
|
|
seq(Expr, Var, Low, High[, Step]) ⇒ list Increments Var from Low through High by an increment of Step, evaluates Expr, and returns the results as a list. The original contents of Var are still there after The default value for Step = 1. |
Note: To force an approximate result, Handheld: Press / ·.
|
|
Catalog > |
|
|
Generates a list of terms for sequence depVar(Var)=Expr as follows: Increments independent variable Var from Var0 through VarMax by VarStep, evaluates depVar(Var) for corresponding values of Var using the Expr formula and ListOfInitTerms, and returns the results as a list.
Generates a matrix of terms for a system (or list) of sequences ListOfDepVars(Var)=ListOrSystemOfExpr as follows: Increments independent variable Var from Var0 through VarMax by VarStep, evaluates ListOfDepVars(Var) for corresponding values of Var using ListOrSystemOfExpr formula and MatrixOfInitTerms, and returns the results as a matrix. The original contents of Var are unchanged after The default value for VarStep = 1. |
Generate the first 5 terms of the sequence u(n) = u(n-1)2/2, with u(1)=2 and VarStep=1.
Example in which Var0=2:
System of two sequences:
Note: The Void (_) in the initial term matrix above is used to indicate that the initial term for u1(n) is calculated using the explicit sequence formula u1(n)=1/n. |
|
Catalog > |
|
|
Generates a list of terms for a sequence u(n)=Expr(u, n) as follows: Increments n from 1 through nMax by 1, evaluates u(n) for corresponding values of n using the Expr(u, n) formula and ListOfInitTerms, and returns the results as a list.
Generates a list of terms for a non-recursive sequence u(n)=Expr(n) as follows: Increments n from 1 through nMax by 1, evaluates u(n) for corresponding values of n using the Expr(n) formula, and returns the results as a list. If nMax is missing, nMax is set to 2500 If nMax=0, nMax is set to 2500 Note: |
Generate the first 6 terms of the sequence u(n) = u(n-1)/2, with u(1)=2.
|
|
Catalog > |
|
|
setMode(modeNameInteger, settingInteger) ⇒ integer Valid only within a function or program. setMode(modeNameInteger, settingInteger) temporarily sets mode modeNameInteger to the new setting settingInteger, and returns an integer corresponding to the original setting of that mode. The change is limited to the duration of the program/function’s execution. modeNameInteger specifies which mode you want to set. It must be one of the mode integers from the table below. settingInteger specifies the new setting for the mode. It must be one of the setting integers listed below for the specific mode you are setting. setMode(list) lets you change multiple settings. list contains pairs of mode integers and setting integers. setMode(list) returns a similar list whose integer pairs represent the original modes and settings. If you have saved all mode settings with getMode(0)→var, you can use setMode(var) to restore those settings until the function or program exits. See getMode(), here. Note: The current mode settings are passed to called subroutines. If any subroutine changes a mode setting, the mode change will be lost when control returns to the calling routine. Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook. |
Display approximate value of π using the default setting for Display Digits, and then display π with a setting of Fix2. Check to see that the default is restored after the program executes.
|
|
Mode |
Mode |
|
|
Display Digits |
1 |
1=Float, 2=Float1, 3=Float2, 4=Float3, 5=Float4, 6=Float5, 7=Float6, 8=Float7, 9=Float8, 10=Float9, 11=Float10, 12=Float11, 13=Float12, 14=Fix0, 15=Fix1, 16=Fix2, 17=Fix3, 18=Fix4, 19=Fix5, 20=Fix6, 21=Fix7, 22=Fix8, 23=Fix9, 24=Fix10, 25=Fix11, 26=Fix12 |
|
Angle |
2 |
1=Radian, 2=Degree, 3=Gradian |
|
Exponential Format |
3 |
1=Normal, 2=Scientific, 3=Engineering |
|
Real or Complex |
4 |
1=Real, 2=Rectangular, 3=Polar |
|
Auto or Approx. |
5 |
1=Auto, 2=Approximate |
|
Vector Format |
6 |
1=Rectangular, 2=Cylindrical, 3=Spherical |
|
Base |
7 |
1=Decimal, 2=Hex, 3=Binary |
|
Catalog > |
|
|
shift(Integer1[,#ofShifts]) ⇒ integer Shifts the bits in a binary integer. You can enter Integer1 in any number base; it is converted automatically to a signed, 64-bit binary form. If the magnitude of Integer1 is too large for this form, a symmetric modulo operation brings it within the range. For more information, see ►Base2, here. If #ofShifts is positive, the shift is to the left. If #ofShifts is negative, the shift is to the right. The default is −1 (shift right one bit). In a right shift, the rightmost bit is dropped and 0 or 1 is inserted to match the leftmost bit. In a left shift, the leftmost bit is dropped and 0 is inserted as the rightmost bit. For example, in a right shift: Each bit shifts right. 0b0000000000000111101011000011010 Inserts 0 if leftmost bit is 0, produces: 0b00000000000000111101011000011010 The result is displayed according to the Base mode. Leading zeros are not shown. |
In Bin base mode:
Important: To enter a binary or hexadecimal number, always use the 0b or 0h prefix (zero, not the letter O). |
|
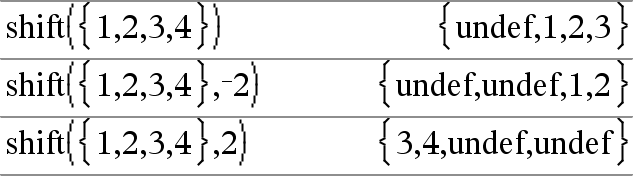
shift(List1[,#ofShifts]) ⇒ list Returns a copy of List1 shifted right or left by #ofShifts elements. Does not alter List1. If #ofShifts is positive, the shift is to the left. If #ofShifts is negative, the shift is to the right. The default is −1 (shift right one element). Elements introduced at the beginning or end of list by the shift are set to the symbol “undef”. |
In Dec base mode:
|
|
shift(String1[,#ofShifts]) ⇒ string Returns a copy of String1 shifted right or left by #ofShifts characters. Does not alter String1. If #ofShifts is positive, the shift is to the left. If #ofShifts is negative, the shift is to the right. The default is −1 (shift right one character). Characters introduced at the beginning or end of string by the shift are set to a space. |
|
|
Catalog > |
|
|
For real and complex Value1, returns Value1 / abs(Value1) when Value1 ≠ 0. Returns 1 if Value1is positive.Returns −1 if Value1 is negative. sign(0) returns „1 if the complex format mode is Real; otherwise, it returns itself. sign(0) represents the unit circle in the complex domain. For a list or matrix, returns the signs of all the elements. |
|
|
Catalog > |
|||||||
|
simult(coeffMatrix, constVector[, Tol]) ⇒ matrix Returns a column vector that contains the solutions to a system of linear equations. Note: See also coeffMatrix must be a square matrix that contains the coefficients of the equations. constVector must have the same number of rows (same dimension) as coeffMatrix and contain the constants. Optionally, any matrix element is treated as zero if its absolute value is less than Tol. This tolerance is used only if the matrix has floating-point entries and does not contain any symbolic variables that have not been assigned a value. Otherwise, Tol is ignored.
|
Solve for x and y:
The solution is x=−3 and y=2.
|
||||||
|
simult(coeffMatrix, constMatrix[, Tol]) ⇒ matrix Solves multiple systems of linear equations, where each system has the same equation coefficients but different constants. Each column in constMatrix must contain the constants for a system of equations. Each column in the resulting matrix contains the solution for the corresponding system. |
Solve: x + 2y = 2
For the first system, x=−3 and y=2. For the second system, x=−7 and y=9/2. |
|
µ key |
|
|
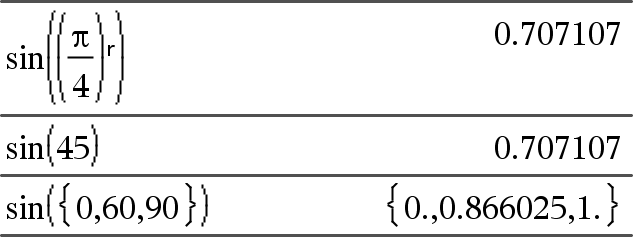
sin(Value1) returns the sine of the argument. sin(List1) returns a list of the sines of all elements in List1. Note: The argument is interpreted as a degree, gradian or radian angle, according to the current angle mode. You can use °, g, or r to override the angle mode setting temporarily. |
In Degree angle mode:
|
|
sin(squareMatrix1) ⇒ squareMatrix Returns the matrix sine of squareMatrix1. This is not the same as calculating the sine of each element. For information about the calculation method, refer to squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode:
|
|
µ key |
|
|
sin-1(Value1) returns the angle whose sine is Value1. sin-1(List1) returns a list of the inverse sines of each element of List1. Note: The result is returned as a degree, gradian or radian angle, according to the current angle mode setting. Note: You can insert this function from the keyboard by typing arcsin(...). |
In Degree angle mode:
|
|
sin-1(squareMatrix1) ⇒ squareMatrix Returns the matrix inverse sine of squareMatrix1. This is not the same as calculating the inverse sine of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode and Rectangular complex format mode:
|
|
Catalog > |
|
|
sinh (Value1) returns the hyperbolic sine of the argument. sinh (List1) returns a list of the hyperbolic sines of each element of List1. |
|
|
sinh(squareMatrix1) ⇒ squareMatrix Returns the matrix hyperbolic sine of squareMatrix1. This is not the same as calculating the hyperbolic sine of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode:
|
|
Catalog > |
|
|
sinh-1(Value1) returns the inverse hyperbolic sine of the argument. sinh-1(List1) returns a list of the inverse hyperbolic sines of each element of List1. Note: You can insert this function from the keyboard by typing arcsinh(...). |
|
|
sinh-1(squareMatrix1) ⇒ squareMatrix Returns the matrix inverse hyperbolic sine of squareMatrix1. This is not the same as calculating the inverse hyperbolic sine of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
In Radian angle mode:
|
|
Catalog > |
|
|
SinReg X, Y[, [Iterations],[Period][, Category, Include]] Computes the sinusoidal regression on lists X and Y. A summary of results is stored in the stat.results variable. (See here.) All the lists must have equal dimension except for Include. X and Y are lists of independent and dependent variables. Iterations is a value that specifies the maximum number of times (1 through 16) a solution will be attempted. If omitted, 8 is used. Typically, larger values result in better accuracy but longer execution times, and vice versa. Period specifies an estimated period. If omitted, the difference between values in X should be equal and in sequential order. If you specify Period, the differences between x values can be unequal. Category is a list of Include is a list of one or more of the category codes. Only those data items whose category code is included in this list are included in the calculation. The output of SinReg is always in radians, regardless of the angle mode setting. For information on the effect of empty elements in a list, see “Empty (Void) Elements,” here. |
|
|
Output variable |
Description |
|
stat.RegEqn |
Regression Equation: a•sin(bx+c)+d |
|
stat.a, stat.b, stat.c, stat.d |
Regression coefficients |
|
stat.Resid |
Residuals from the regression |
|
stat.XReg |
List of data points in the modified X List actually used in the regression based on restrictions of Freq, Category List, and Include Categories |
|
stat.YReg |
List of data points in the modified Y List actually used in the regression based on restrictions of Freq, Category List, and Include Categories |
|
stat.FreqReg |
List of frequencies corresponding to stat.XReg and stat.YReg |
|
Catalog > |
|
|
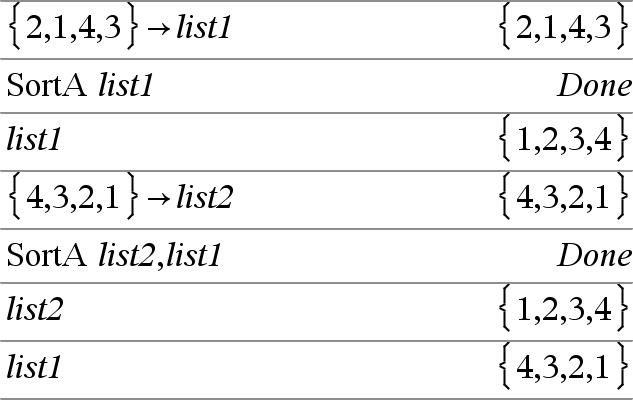
SortA List1[, List2] [, List3]... Sorts the elements of the first argument in ascending order. If you include additional arguments, sorts the elements of each so that their new positions match the new positions of the elements in the first argument. All arguments must be names of lists or vectors. All arguments must have equal dimensions. Empty (void) elements within the first argument move to the bottom. For more information on empty elements, see here. |
|
|
Catalog > |
|
|
SortD List1[, List2][, List3]... Identical to SortA, except SortD sorts the elements in descending order. Empty (void) elements within the first argument move to the bottom. For more information on empty elements, see here. |
|
|
Catalog > |
|
|
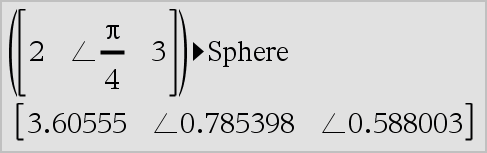
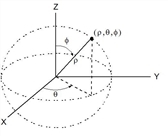
Vector►Sphere Note: You can insert this operator from the computer keyboard by typing @>Sphere. Displays the row or column vector in spherical form [ρ∠θ∠φ]. Vector must be of dimension 3 and can be either a row or a column vector. Note: ►Sphere is a display-format instruction, not a conversion function. You can use it only at the end of an entry line. |
|
|
Catalog > |
|
|
Returns the square root of the argument. For a list, returns the square roots of all the elements in List1. Note: See also Square root template, here. |
|
|
Catalog > |
|
|
stat.results Displays results from a statistics calculation. The results are displayed as a set of name-value pairs. The specific names shown are dependent on the most recently evaluated statistics function or command. You can copy a name or value and paste it into other locations.
Note: Avoid defining variables that use the same names as those used for statistical analysis. In some cases, an error condition could occur. Variable names used for statistical analysis are listed in the table below. |
|
|
stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.χ² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d |
stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX |
stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n Stat.Ç stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y |
stat.Q3X stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.σx stat.σy stat.σx1 stat.σx2 stat.Σx stat.Σx² stat.Σxy stat.Σy stat.Σy² stat.s stat.SE stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS |
stat.SSBlock stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1 stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w stat.y stat.yList stat.YReg |
|
Note: Each time the Lists & Spreadsheet application calculates statistical results, it copies the “stat.” group variables to a “stat#.” group, where # is a number that is incremented automatically. This lets you maintain previous results while performing multiple calculations. |
|
Catalog > |
|
|
stat.values Displays a matrix of the values calculated for the most recently evaluated statistics function or command. Unlike stat.results, stat.values omits the names associated with the values. You can copy a value and paste it into other locations. |
See the stat.results example. |
|
Catalog > |
|
|
stDevPop(List [, freqList]) ⇒ expression Returns the population standard deviation of the elements in List. Each freqList element counts the number of consecutive occurrences of the corresponding element in List. Note:List must have at least two elements. Empty (void) elements are ignored. For more information on empty elements, see here. |
In Radian angle and auto modes:
|
|
stDevPop(Matrix1[, freqMatrix]) ⇒ matrix Returns a row vector of the population standard deviations of the columns in Matrix1. Each freqMatrix element counts the number of consecutive occurrences of the corresponding element in Matrix1. Note:Matrix1must have at least two rows. Empty (void) elements are ignored. For more information on empty elements, see here. |
|
|
Catalog > |
|
|
stDevSamp(List[, freqList]) ⇒ expression Returns the sample standard deviation of the elements in List. Each freqList element counts the number of consecutive occurrences of the corresponding element in List. Note:List must have at least two elements. Empty (void) elements are ignored. For more information on empty elements, see here. |
|
|
stDevSamp(Matrix1[, freqMatrix]) ⇒ matrix Returns a row vector of the sample standard deviations of the columns in Matrix1. Each freqMatrix element counts the number of consecutive occurrences of the corresponding element in Matrix1. Note:Matrix1must have at least two rows. Empty (void) elements are ignored. For more information on empty elements, see here. |
|
|
Catalog > |
|
|
Stop Programming command: Terminates the program. Stop is not allowed in functions. Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook. |
|
|
See →(store), here. |
|
|
|
|
|
Catalog > |
|
|
string(Expr) ⇒ string Simplifies Expr and returns the result as a character string. |
|
|
Catalog > |
|
|
subMat(Matrix1[, startRow][, startCol][, endRow][, endCol]) ⇒ matrix Returns the specified submatrix of Matrix1. Defaults: startRow=1, startCol=1, endRow=last row, endCol=last column. |
|
|
Sum (Sigma) |
See Σ(), here. |
|
|
|
|
Catalog > |
|
|
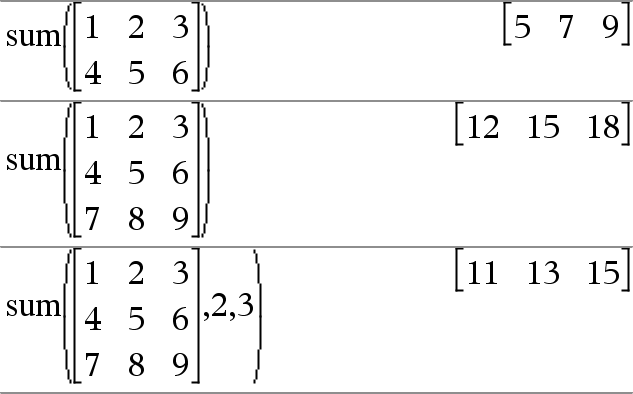
sum(List[, Start[, End]]) ⇒ expression Returns the sum of all elements in List. Start and End are optional. They specify a range of elements. Any void argument produces a void result. Empty (void) elements in List are ignored. For more information on empty elements, see here. |
|
|
sum(Matrix1[, Start[, End]]) ⇒ matrix Returns a row vector containing the sums of all elements in the columns in Matrix1. Start and End are optional. They specify a range of rows. Any void argument produces a void result. Empty (void) elements in Matrix1 are ignored. For more information on empty elements, see here. |
|
|
Catalog > |
|||||||
|
sumIf(List,Criteria[, SumList]) ⇒ value Returns the accumulated sum of all elements in List that meet the specified Criteria. Optionally, you can specify an alternate list, sumList, to supply the elements to accumulate. List can be an expression, list, or matrix. SumList, if specified, must have the same dimension(s) as List. Criteria can be:
When a List element meets the Criteria, the element is added to the accumulating sum. If you include sumList, the corresponding element from sumList is added to the sum instead. Within the Lists & Spreadsheet application, you can use a range of cells in place of List and sumList. Empty (void) elements are ignored. For more information on empty elements, see here. Note: See also countIf(), here. |
|
|
See Σ(), here. |
|
|
|
|
|
Catalog > |
|
|
system(Value1[, Value2[, Value3[, ...]]]) Returns a system of equations, formatted as a list. You can also create a system by using a template. |
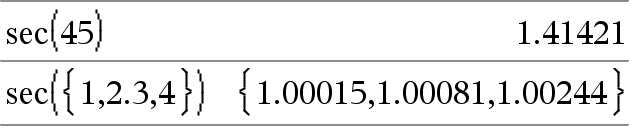


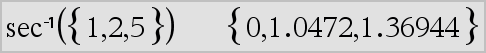






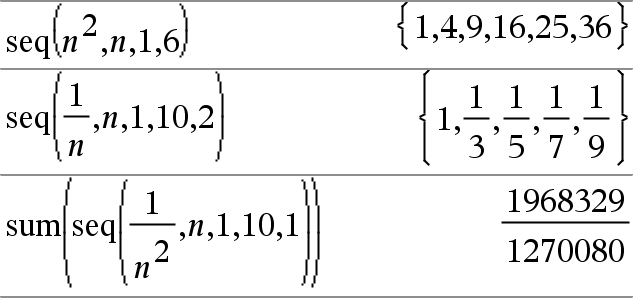
 .
.