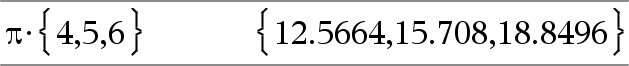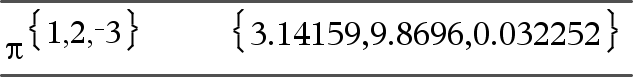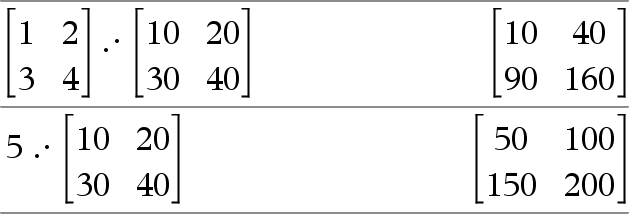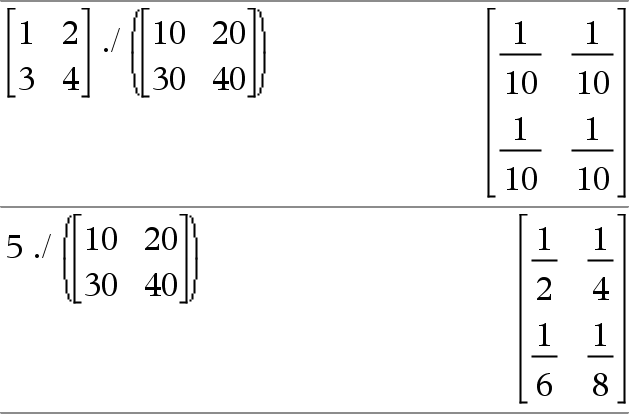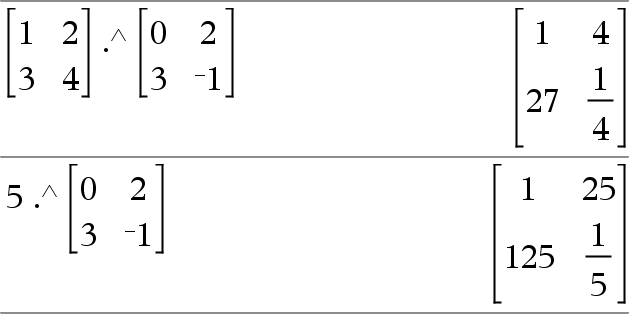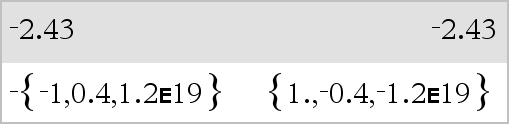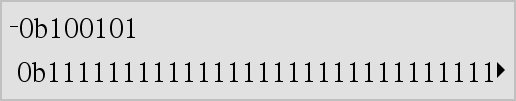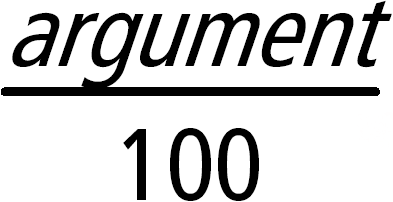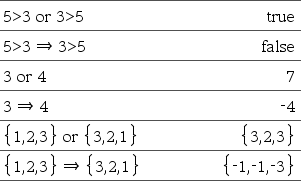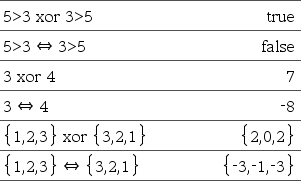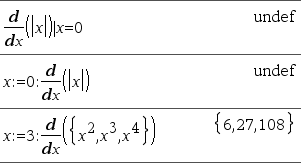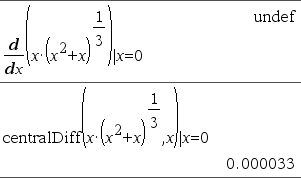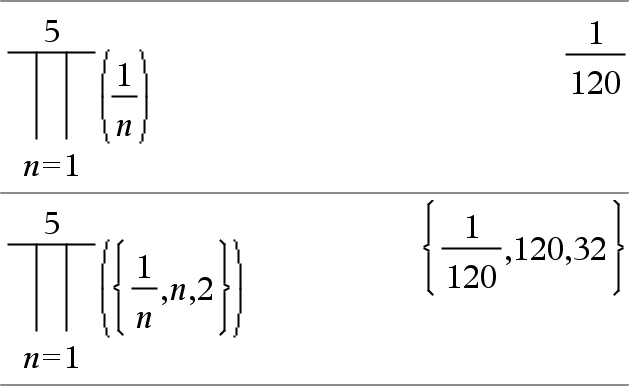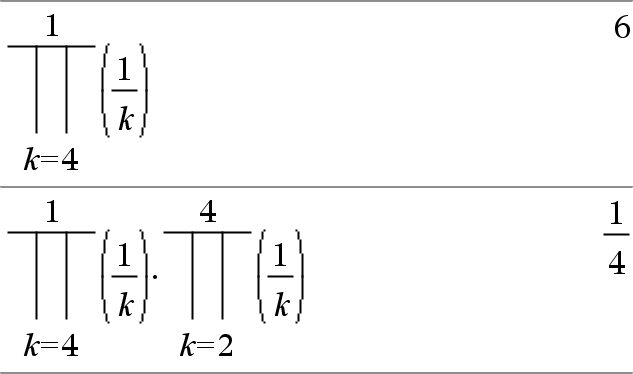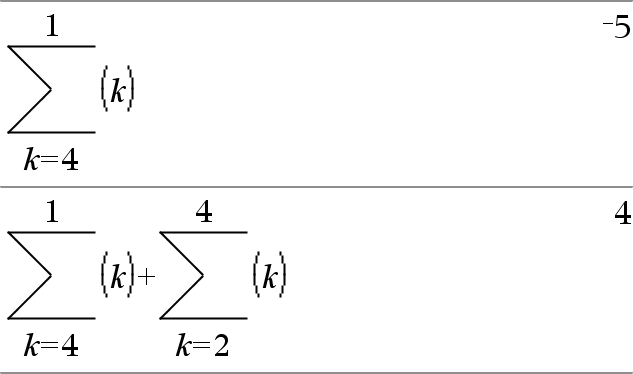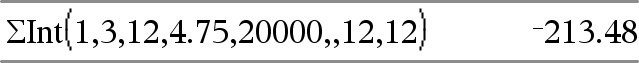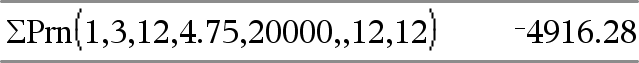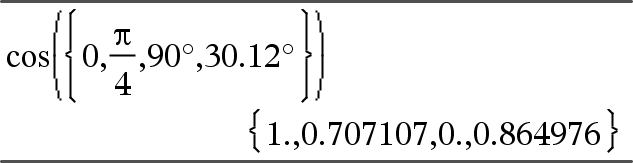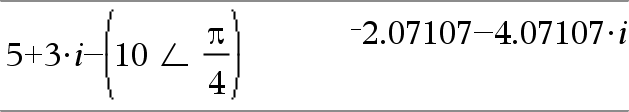|
+ key |
|
|
Value1 + Value2 ⇒ value Returns the sum of the two arguments. |
|
|
List1 + List2 ⇒ list Matrix1 + Matrix2 ⇒ matrix Returns a list (or matrix) containing the sums of corresponding elements in List1 and List2 (or Matrix1 and Matrix2). Dimensions of the arguments must be equal. |
|
|
Value + List1 ⇒ list List1 + Value ⇒ list
|
|
|
Value + Matrix1 ⇒ matrix Matrix1 + Value ⇒ matrix Returns a matrix with Value added to each element on the diagonal of Matrix1. Matrix1 must be square. Note: Use .+ (dot plus) to add an expression to each element. |
|
|
- key |
|
|
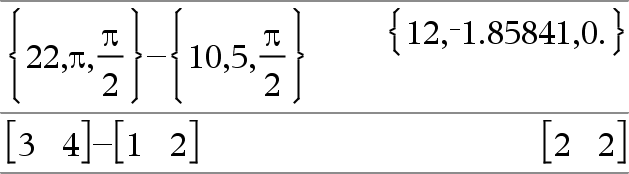
Value1−Value2 ⇒ value Returns Value1 minus Value2. |
|
|
List1 −List2⇒ list Matrix1 −Matrix2 ⇒ matrix Subtracts each element in List2 (or Matrix2) from the corresponding element in List1 (or Matrix1), and returns the results. Dimensions of the arguments must be equal. |
|
|
Value − List1 ⇒ list List1 − Value ⇒ list Subtracts each List1 element from Value or subtracts Value from each List1 element, and returns a list of the results. |
|
|
Value − Matrix1 ⇒ matrix Matrix1 − Value ⇒ matrix Value − Matrix1 returns a matrix of Value times the identity matrix minus Matrix1. Matrix1 must be square. Matrix1 − Value returns a matrix of Value times the identity matrix subtracted from Matrix1. Matrix1 must be square. Note: Use .− (dot minus) to subtract an expression from each element. |
|
|
r key |
|
|
Value1•Value2 ⇒ value Returns the product of the two arguments. |
|
|
List1•List2 ⇒ list Returns a list containing the products of the corresponding elements in List1 and List2. Dimensions of the lists must be equal. |
|
|
Matrix1•Matrix2 ⇒ matrix Returns the matrix product of Matrix1 and Matrix2. The number of columns in Matrix1 must equal the number of rows in Matrix2. |
|
|
|
|
|
Returns a matrix containing the products of Value and each element in Matrix1. Note: Use .•(dot multiply) to multiply an expression by each element. |
|
|
p key |
|
|
Value1 ⁄ Value2 ⇒ value Returns the quotient of Value1 divided by Value2. Note: See also Fraction template, here. |
|
|
List1 ⁄ List2 ⇒ list Returns a list containing the quotients of List1 divided by List2. Dimensions of the lists must be equal. |
|
|
Value ⁄ List1 ⇒ list List1 ⁄ Value ⇒ list Returns a list containing the quotients of Value divided by List1 or List1 divided by Value. |
|
|
Value ⁄ Matrix1 ⇒ matrix Matrix1 ⁄ Value ⇒ matrix Returns a matrix containing the quotients of Matrix1 ⁄ Value. Note: Use . ⁄ (dot divide) to divide an expression by each element. |
|
|
l key |
|
|
List1 ^ List2 ⇒ list Returns the first argument raised to the power of the second argument. Note: See also Exponent template, here. For a list, returns the elements in List1 raised to the power of the corresponding elements in List2. In the real domain, fractional powers that have reduced exponents with odd denominators use the real branch versus the principal branch for complex mode. |
|
|
|
|
|
|
|
|
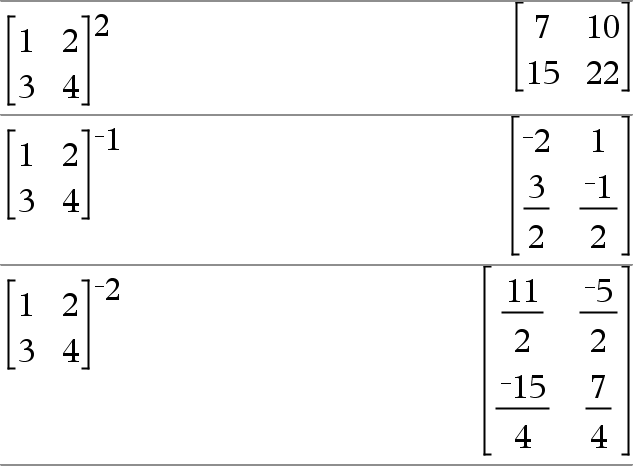
squareMatrix1 ^ integer ⇒ matrix Returns squareMatrix1 raised to the integer power. squareMatrix1 must be a square matrix. If integer = −1, computes the inverse matrix. |
|
|
q key |
|
|
Returns the square of the argument. List12 ⇒ list Returns a list containing the squares of the elements in List1. squareMatrix12 ⇒ matrix Returns the matrix square of squareMatrix1. This is not the same as calculating the square of each element. Use .^2 to calculate the square of each element. |
|
|
^+ keys |
|
|
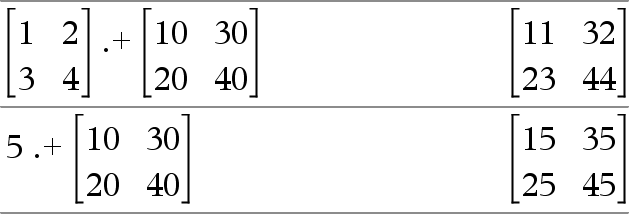
Matrix1 .+ Matrix2 ⇒ matrix
Matrix1.+Matrix2 returns a matrix that is the sum of each pair of corresponding elements in Matrix1 and Matrix2.
|
|
|
^- keys |
|
|
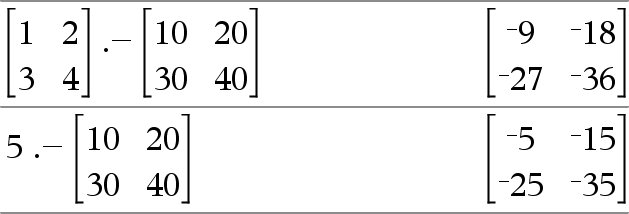
Matrix1 .− Matrix2⇒ matrix
Matrix1.− Matrix2 returns a matrix that is the difference between each pair of corresponding elements in Matrix1 and Matrix2.
|
|
|
^r keys |
|
|
Matrix1 .• Matrix2⇒ matrix
Matrix1.• Matrix2 returns a matrix that is the product of each pair of corresponding elements in Matrix1 and Matrix2.
|
|
|
^p keys |
|
|
Matrix1. ⁄ Matrix2 ⇒ matrix Value . ⁄ Matrix1⇒ matrix Matrix1 . ⁄ Matrix2 returns a matrix that is the quotient of each pair of corresponding elements in Matrix1 and Matrix2. Value . ⁄ Matrix1 returns a matrix that is the quotient of Value and each element in Matrix1. |
|
|
^l keys |
|
|
Matrix1 .^ Matrix2 ⇒ matrix
Matrix1.^ Matrix2 returns a matrix where each element in Matrix2 is the exponent for the corresponding element in Matrix1.
|
|
|
v key |
|
|
−
−List1 ⇒ list −Matrix1 ⇒ matrix Returns the negation of the argument. For a list or matrix, returns all the elements negated. If the argument is a binary or hexadecimal integer, the negation gives the two’s complement. |
Important: Zero, not the letter O.
To see the entire result, |
|
/k keys |
|
|
List1% ⇒ list Matrix1% ⇒ matrix Returns For a list or matrix, returns a list or matrix with each element divided by 100. |
|
|
= key |
|
|
Expr1=Expr2 ⇒ Boolean expression List1=List2 ⇒ Boolean list Matrix1=Matrix2 ⇒ Boolean matrix Returns true if Expr1 is determined to be equal to Expr2. Returns false if Expr1 is determined to not be equal to Expr2. Anything else returns a simplified form of the equation. For lists and matrices, returns comparisons element by element. Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook. |
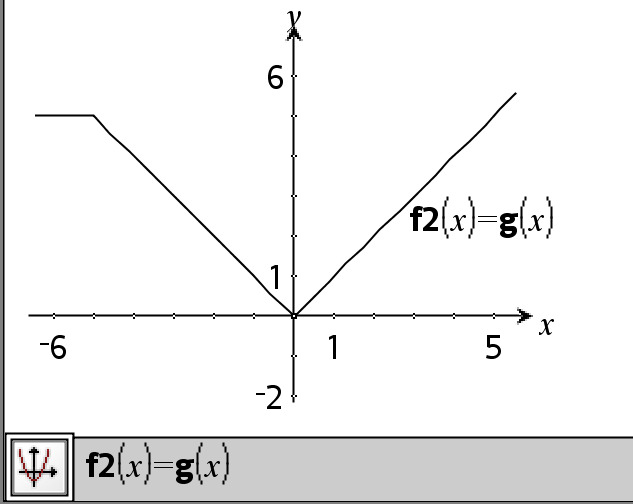
Example function that uses math test symbols: =, ≠, <, ≤, >, ≥
Result of graphing g(x)
|
|
/= keys |
|
|
Expr1≠Expr2 ⇒ Boolean expression List1≠List2 ⇒ Boolean list Matrix1≠Matrix2 ⇒ Boolean matrix Returns true if Expr1 is determined to be not equal to Expr2. Returns false if Expr1 is determined to be equal to Expr2. Anything else returns a simplified form of the equation. For lists and matrices, returns comparisons element by element. Note: You can insert this operator from the keyboard by typing /= |
See “=” (equal) example. |
|
/= keys |
|
|
Expr1<Expr2 ⇒ Boolean expression List1<List2 ⇒ Boolean list Matrix1<Matrix2 ⇒ Boolean matrix Returns true if Expr1 is determined to be less than Expr2. Returns false if Expr1 is determined to be greater than or equal to Expr2. Anything else returns a simplified form of the equation. For lists and matrices, returns comparisons element by element. |
See “=” (equal) example. |
|
/= keys |
|
|
Expr1≤Expr2 ⇒ Boolean expression List1≤List2 ⇒ Boolean list Matrix1 ≤Matrix2 ⇒ Boolean matrix Returns true if Expr1 is determined to be less than or equal to Expr2. Returns false if Expr1 is determined to be greater than Expr2. Anything else returns a simplified form of the equation. For lists and matrices, returns comparisons element by element. Note: You can insert this operator from the keyboard by typing <= |
See “=” (equal) example. |
|
/= keys |
|
|
Expr1>Expr2 ⇒ Boolean expression List1>List2 ⇒ Boolean list Matrix1>Matrix2 ⇒ Boolean matrix Returns true if Expr1 is determined to be greater than Expr2. Returns false if Expr1 is determined to be less than or equal to Expr2. Anything else returns a simplified form of the equation. For lists and matrices, returns comparisons element by element. |
See “=” (equal) example. |
|
/= keys |
|
|
Expr1≥Expr2 ⇒ Boolean expression List1≥List2 ⇒ Boolean list Matrix1 ≥Matrix2 ⇒ Boolean matrix Returns true if Expr1 is determined to be greater than or equal to Expr2. Returns false if Expr1 is determined to be less than Expr2. Anything else returns a simplified form of the equation. For lists and matrices, returns comparisons element by element. Note: You can insert this operator from the keyboard by typing >= |
See “=” (equal) example. |
|
/= keys |
|
|
BooleanExpr1 ⇒ BooleanExpr2 returns Boolean expression BooleanList1 ⇒ BooleanList2 returns Boolean list BooleanMatrix1 ⇒ BooleanMatrix2 returns Boolean matrix Integer1 ⇒ Integer2 returns Integer Evaluates the expression not <argument1> or <argument2> and returns true, false, or a simplified form of the equation. For lists and matrices, returns comparisons element by element. Note: You can insert this operator from the keyboard by typing => |
|
|
/= keys |
|
|
BooleanExpr1 ⇔ BooleanExpr2 returns Boolean expression BooleanList1 ⇔ BooleanList2 returns Boolean list BooleanMatrix1 ⇔ BooleanMatrix2 returns Boolean matrix Integer1 ⇔ Integer2 returns Integer Returns the negation of an XOR Boolean operation on the two arguments. Returns true, false, or a simplified form of the equation. For lists and matrices, returns comparisons element by element. Note: You can insert this operator from the keyboard by typing <=> |
|
|
º key |
|
|
List1! ⇒ list Matrix1! ⇒ matrix Returns the factorial of the argument. For a list or matrix, returns a list or matrix of factorials of the elements. |
|
|
/k keys |
|
|
String1 & String2 ⇒ string Returns a text string that is String2 appended to String1. |
|
|
Catalog > |
|
|
d(Expr1, Var[, Order]) ⇒ value d(List1, Var[, Order]) ⇒ list d(Matrix1, Var[, Order]) ⇒ matrix Except when using the first syntax, you must store a numeric value in variable Var before evaluating d(). Refer to the examples.
Order, if included, must be=1 or 2. The default is 1. Note: You can insert this function from the keyboard by typing Note: See also First derivative, here or Second derivative, here. |
|
|
Consider the example on the right. The first derivative of x•(x^2+x)^(1/3) at x=0 is equal to 0. However, because the first derivative of the subexpression (x^2+x)^(1/3) is undefined at x=0, and this value is used to calculate the derivative of the total expression, d() reports the result as undefined and displays a warning message.
|
|
|
Catalog > |
|
|
∫(Expr1, Var, Lower,Upper) ⇒ value Returns the integral of Expr1 with respect to the variable Var from Lower to Upper. Can be used to calculate the definite integral numerically, using the same method as nInt(). Note: You can insert this function from the keyboard by typing integral(...). Note: See also nInt(), here, and Definiteintegral template, here. |
|
|
/q keys |
|
|
√(List1) ⇒ list Returns the square root of the argument. For a list, returns the square roots of all the elements in List1. Note: You can insert this function from the keyboard by typing sqrt(...) Note: See also Square root template, here. |
|
|
Catalog > |
|
|
Π(Expr1, Var, Low, High) ⇒ expression Note: You can insert this function from the keyboard by typing prodSeq(...). Evaluates Expr1 for each value of Var from Low to High, and returns the product of the results. Note: See also Product template (Π), here. |
|
|
Π(Expr1, Var, Low, Low−1) ⇒ 1 Π(Expr1, Var, Low, High) ⇒ 1/Π(Expr1, Var, High+1, Low−1) if High < Low−1
The product formulas used are derived from the following reference: Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catalog > |
|
|
Σ(Expr1, Var, Low, High) ⇒ expression Note: You can insert this function from the keyboard by typing sumSeq(...). Evaluates Expr1 for each value of Var from Low to High, and returns the sum of the results. Note: See also Sum template, here. |
|
|
Σ(Expr1, Var, Low, Low−1) ⇒ 0 Σ(Expr1, Var, Low, High) ⇒ μ Σ(Expr1, Var, High+1, Low−1) if High < Low−1
The summation formulas used are derived from the following reference: Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catalog > |
||||||||||
|
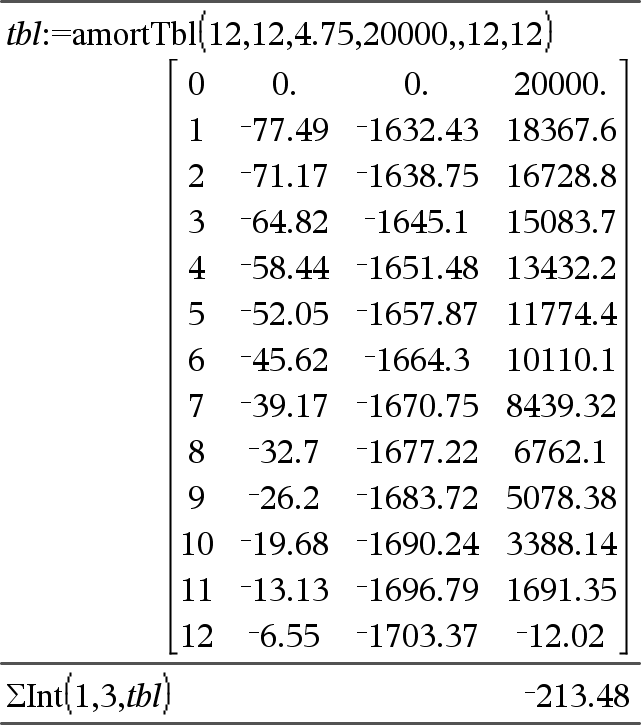
ΣInt(NPmt1, NPmt2, N, I, PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt], [roundValue]) ⇒ value ΣInt(NPmt1,NPmt2,amortTable) ⇒ value Amortization function that calculates the sum of the interest during a specified range of payments. NPmt1 and NPmt2 define the start and end boundaries of the payment range. N, I, PV, Pmt, FV, PpY, CpY, and PmtAt are described in the table of TVM arguments, here.
roundValue specifies the number of decimal places for rounding. Default=2. ΣInt(NPmt1,NPmt2,amortTable) calculates the sum of the interest based on amortization table amortTable. The amortTable argument must be a matrix in the form described under amortTbl(), here. Note: See also ΣPrn(), below, and Bal(), here. |
|
|
Catalog > |
||||||||||
|
ΣPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [roundValue]) ⇒ value ΣPrn(NPmt1, NPmt2, amortTable) ⇒ value Amortization function that calculates the sum of the principal during a specified range of payments. NPmt1 and NPmt2 define the start and end boundaries of the payment range. N, I, PV, Pmt, FV, PpY, CpY, and PmtAt are described in the table of TVM arguments, here.
roundValue specifies the number of decimal places for rounding. Default=2. ΣPrn(NPmt1,NPmt2,amortTable) calculates the sum of the principal paid based on amortization table amortTable. The amortTable argument must be a matrix in the form described under amortTbl(), here. Note: See also ΣInt(), above, and Bal(), here. |
|
|
/k keys |
|
|
# varNameString Refers to the variable whose name is varNameString. This lets you use strings to create variable names from within a function. |
Creates or refers to the variable xyz .
Returns the value of the variable (r) whose name is stored in variable s1. |
|
i key |
|
|
mantissaEexponent Enters a number in scientific notation. The number is interpreted as mantissa × 10exponent. Hint: If you want to enter a power of 10 without causing a decimal value result, use 10^integer. Note: You can insert this operator from the computer keyboard by typing @E. for example, type 2.3@E4 to enter 2.3E4. |
|
|
1 key |
|
|
List1g ⇒ list Matrix1g ⇒ matrix This function gives you a way to specify a gradian angle while in the Degree or Radian mode. In Radian angle mode, multiplies Expr1 by π/200. In Degree angle mode, multiplies Expr1 by g/100. In Gradian mode, returns Expr1 unchanged. Note: You can insert this symbol from the computer keyboard by typing @g. |
In Degree, Gradian or Radian mode:
|
|
1 key |
|
|
List1r ⇒ list Matrix1r ⇒ matrix This function gives you a way to specify a radian angle while in Degree or Gradian mode. In Degree angle mode, multiplies the argument by 180/π. In Radian angle mode, returns the argument unchanged. In Gradian mode, multiplies the argument by 200/π. Hint: Use r if you want to force radians in a function definition regardless of the mode that prevails when the function is used. Note: You can insert this symbol from the computer keyboard by typing @r. |
In Degree, Gradian or Radian angle mode:
|
|
1 key |
|
|
List1° ⇒ list Matrix1° ⇒ matrix This function gives you a way to specify a degree angle while in Gradian or Radian mode. In Radian angle mode, multiplies the argument by π/180. In Degree angle mode, returns the argument unchanged. In Gradian angle mode, multiplies the argument by 10/9. Note: You can insert this symbol from the computer keyboard by typing @d. |
In Degree, Gradian or Radian angle mode:
In Radian angle mode:
|
|
/k keys |
|||||||
|
dd°mm'ss.ss'' ⇒ expression dd A positive or negative number Returns dd+(mm/60)+(ss.ss/3600). This base‑60 entry format lets you:
Note: Follow ss.ss with two apostrophes (''), not a quote symbol ("). |
In Degree angle mode:
|
|
/k keys |
|
|
[Radius,∠θ_Angle] ⇒ vector [Radius,∠θ_Angle,Z_Coordinate] ⇒ vector [Radius,∠θ_Angle,∠θ_Angle] ⇒ vector Returns coordinates as a vector depending on the Vector Format mode setting: rectangular, cylindrical, or spherical. Note: You can insert this symbol from the computer keyboard by typing @<. |
In Radian mode and vector format set to:
|
|
(Magnitude∠Angle) ⇒ complexValue Enters a complex value in (r∠θ) polar form. The Angle is interpreted according to the current Angle mode setting. |
In Radian angle mode and Rectangular complex format:
|
|
_ (underscore as an empty element) |
See “Empty (Void) Elements,” here. |
|
|
|
|
Catalog > |
|
|
10^ (List1) ⇒ list Returns 10 raised to the power of the argument. For a list, returns 10 raised to the power of the elements in List1. |
|
|
10^(squareMatrix1) ⇒ squareMatrix Returns 10 raised to the power of squareMatrix1. This is not the same as calculating 10 raised to the power of each element. For information about the calculation method, refer to cos(). squareMatrix1 must be diagonalizable. The result always contains floating-point numbers. |
|
|
Catalog > |
|
|
List1 ^-1 ⇒ list Returns the reciprocal of the argument. For a list, returns the reciprocals of the elements in List1. |
|
|
squareMatrix1 ^-1 ⇒ squareMatrix Returns the inverse of squareMatrix1. squareMatrix1 must be a non-singular square matrix. |
|
|
/k keys |
||||||||||
|
Expr | BooleanExpr1[ Expr | BooleanExpr1[ The constraint (“|”) symbol serves as a binary operator. The operand to the left of | is an expression. The operand to the right of | specifies one or more relations that are intended to affect the simplification of the expression. Multiple relations after | must be joined by logical “ The constraint operator provides three basic types of functionality:
|
|
|||||||||
|
Substitutions are in the form of an equality, such as x=3 or y=sin(x). To be most effective, the left side should be a simple variable. Expr | Variable = value will substitute value for every occurrence of Variable in Expr. |
|
|||||||||
|
Interval constraints take the form of one or more inequalities joined by logical “and” or “or” operators. Interval constraints also permit simplification that otherwise might be invalid or not computable. |
|
|||||||||
|
Exclusions use the “not equals” (/= or ≠) relational operator to exclude a specific value from consideration. |
|
/h key |
|
|
If the variable Var does not exist, creates it and initializes it to Value, List, or Matrix. If the variable Var already exists and is not locked or protected, replaces its contents with Value, List, or Matrix. Note: You can insert this operator from the keyboard by typing =: as a shortcut. For example, type pi/4 =: myvar. |
|
|
/t keys |
|
|
Var := List Var := Matrix Function(Param1,...) := Expr Function(Param1,...) := List Function(Param1,...) := Matrix If variable Var does not exist, creates Var and initializes it to Value, List, or Matrix. If Var already exists and is not locked or protected, replaces its contents with Value, List, or Matrix. |
|
|
/k keys |
|
|
© [text] © processes text as a comment line, allowing you to annotate functions and programs that you create. © can be at the beginning or anywhere in the line. Everything to the right of ©, to the end of the line, is the comment. Note for entering the example: For instructions on entering multi-line program and function definitions, refer to the Calculator section of your product guidebook. |
|
|
0B keys, 0H keys |
|
|
0b binaryNumber Denotes a binary or hexadecimal number, respectively. To enter a binary or hex number, you must enter the 0b or 0h prefix regardless of the Base mode. Without a prefix, a number is treated as decimal (base 10). Results are displayed according to the Base mode. |
In Dec base mode:
|