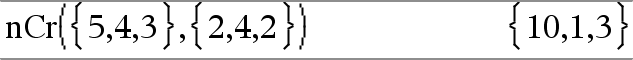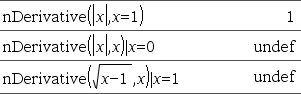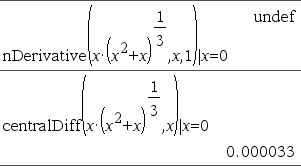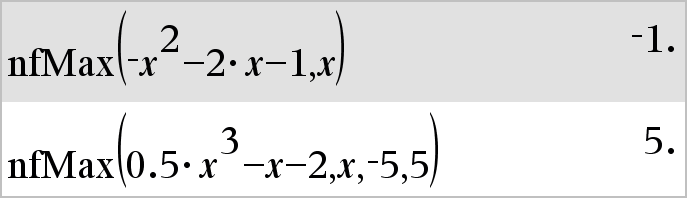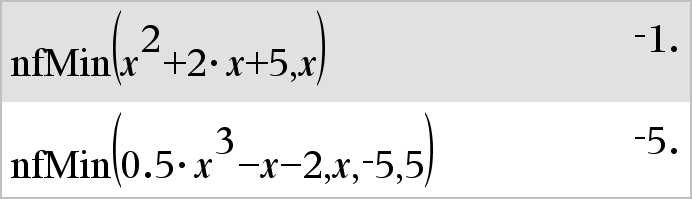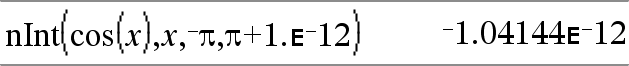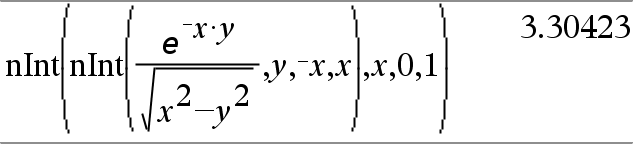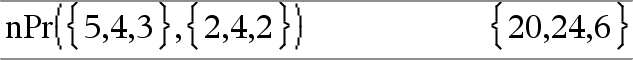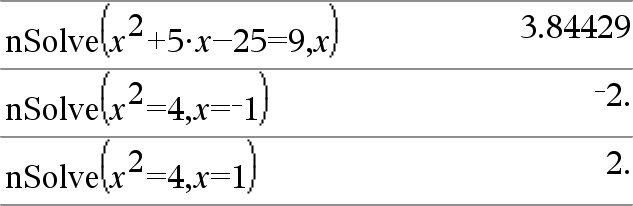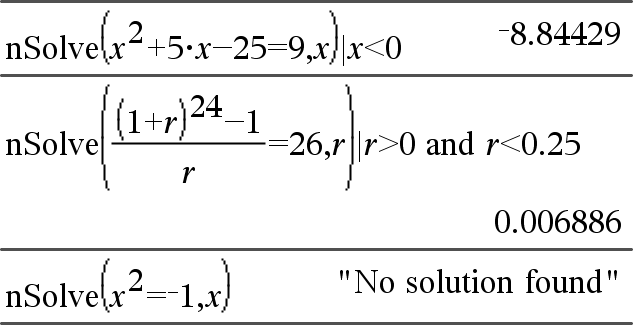|
/= keys |
|
|
BooleanExpr1 Returns the negation of a logical For lists and matrices, returns comparisons element by element. |
|
|
Integer1
Compares two real integers bit-by-bit using a You can enter the integers in any number base. For a binary or hexadecimal entry, you must use the 0b or 0h prefix, respectively. Without a prefix, integers are treated as decimal (base 10). |
|
|
Catalog > |
|
|
nCr(Value1, Value2) ⇒ expression For integer Value1 and Value2 with Value1 ≥ Value2≥ 0, nCr() is the number of combinations of Value1 things taken Value2 at a time. (This is also known as a binomial coefficient.) nCr(Value, 0) ⇒ 1 nCr(Value, negInteger) ⇒ 0 nCr(Value, posInteger) ⇒ Value•(Value−1) ... (Value−posInteger+1)/ posInteger!
|
|
|
nCr(List1, List2) ⇒ list Returns a list of combinations based on the corresponding element pairs in the two lists. The arguments must be the same size list. |
|
|
nCr(Matrix1, Matrix2) ⇒ matrix Returns a matrix of combinations based on the corresponding element pairs in the two matrices. The arguments must be the same size matrix. |
|
|
Catalog > |
|
|
Returns the numerical derivative calculated using auto differentiation methods. When Value is specified, it overrides any prior variable assignment or any current “|” substitution for the variable. If the variable Var does not contain a numeric value, you must provide Value. Order of the derivative must be 1 or 2. |
|
|
Consider the example on the right. The first derivative of x•(x^2+x)^(1/3) at x=0 is equal to 0. However, because the first derivative of the subexpression (x^2+x)^(1/3) is undefined at x=0, and this value is used to calculate the derivative of the total expression, nDerivative() reports the result as undefined and displays a warning message.
|
|
|
Catalog > |
|
|
newList(numElements) ⇒ list Returns a list with a dimension of numElements. Each element is zero. |
|
|
Catalog > |
|
|
newMat(numRows, numColumns) ⇒ matrix Returns a matrix of zeros with the dimension numRows by numColumns. |
|
|
Catalog > |
|
|
nfMax(Expr, Var) ⇒ value Returns a candidate numerical value of variable Var where the local maximum of Expr occurs. If you supply lowBound and upBound, the function looks in the closed interval [lowBound,upBound] for the local maximum. |
|
|
Catalog > |
|
|
nfMin(Expr, Var) ⇒ value Returns a candidate numerical value of variable Var where the local minimum of Expr occurs. If you supply lowBound and upBound, the function looks in the closed interval [lowBound,upBound] for the local minimum. |
|
|
Catalog > |
|
|
nInt(Expr1, Var, Lower, Upper) ⇒ expression If the integrand Expr1 contains no variable other than Var, and if Lower and Upper are constants, positive ∞, or negative ∞, then nInt() returns an approximation of ∫(Expr1, Var, Lower, Upper). This approximation is a weighted average of some sample values of the integrand in the interval Lower<Var<Upper. |
|
|
The goal is six significant digits. The adaptive algorithm terminates when it seems likely that the goal has been achieved, or when it seems unlikely that additional samples will yield a worthwhile improvement. A warning is displayed (“Questionable accuracy”) when it seems that the goal has not been achieved. |
|
|
Nest nInt() to do multiple numeric integration. Integration limits can depend on integration variables outside them. |
|
|
Catalog > |
|
|
nom(effectiveRate,CpY) ⇒ value Financial function that converts the annual effective interest rate effectiveRate to a nominal rate, given CpY as the number of compounding periods per year. effectiveRate must be a real number, and CpY must be a real number > 0. Note: See also eff(), here. |
|
|
/= keys |
|
|
BooleanExpr1
Returns the negation of a logical For lists and matrices, returns comparisons element by element. |
|
|
Integer1
Compares two real integers bit-by-bit using a You can enter the integers in any number base. For a binary or hexadecimal entry, you must use the 0b or 0h prefix, respectively. Without a prefix, integers are treated as decimal (base 10). |
|
|
Catalog > |
|
|
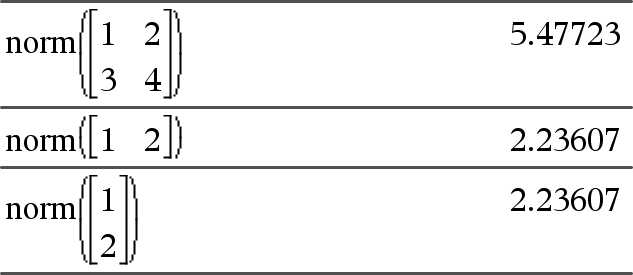
norm(Matrix) ⇒ expression norm(Vector) ⇒ expression Returns the Frobenius norm. |
|
|
Catalog > |
|
|
normCdf(lowBound,upBound[,μ[,σ]]) ⇒ number if lowBound and upBound are numbers, list if lowBound and upBound are lists Computes the normal distribution probability between lowBound and upBound for the specified μ (default=0) and σ (default=1).
|
|
|
Catalog > |
|
|
normPdf(XVal[,μ[,σ]]) ⇒ number if XVal is a number, list if XVal is a list Computes the probability density function for the normal distribution at a specified XVal value for the specified μ and σ. |
|
|
Catalog > |
|
|
not BooleanExpr ⇒ Boolean expression Returns true, false, or a simplified form of the argument. |
|
|
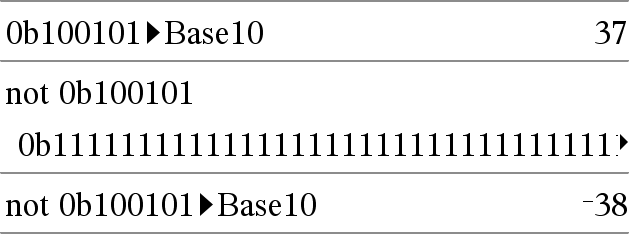
not Integer1 ⇒ integer Returns the one’s complement of a real integer. Internally, Integer1 is converted to a signed, 64-bit binary number. The value of each bit is flipped (0 becomes 1, and vice versa) for the one’s complement. Results are displayed according to the Base mode. You can enter the integer in any number base. For a binary or hexadecimal entry, you must use the 0b or 0h prefix, respectively. Without a prefix, the integer is treated as decimal (base 10). If you enter a decimal integer that is too large for a signed, 64-bit binary form, a symmetric modulo operation is used to bring the value into the appropriate range. For more information, see ►Base2, here. |
In Hex base mode: Important: Zero, not the letter O.
To see the entire result, Note: A binary entry can have up to 64 digits (not counting the 0b prefix). A hexadecimal entry can have up to 16 digits. |
|
Catalog > |
|
|
nPr(Value1, Value2) ⇒ expression For integer Value1 and Value2 with Value1 ≥ Value2 ≥ 0, nPr() is the number of permutations of Value1 things taken Value2 at a time. nPr(Value, 0) ⇒ 1 nPr(Value, negInteger) ⇒ 1 / ((Value+1)•(Value+2)...(Value−negInteger)) nPr(Value, posInteger) ⇒ Value•(Value−1) ... (Value−posInteger+1)
|
|
|
nPr(List1, List2) ⇒ list Returns a list of permutations based on the corresponding element pairs in the two lists. The arguments must be the same size list. |
|
|
nPr(Matrix1, Matrix2) ⇒ matrix Returns a matrix of permutations based on the corresponding element pairs in the two matrices. The arguments must be the same size matrix. |
|
|
Catalog > |
|
|
npv(InterestRate,CFO,CFList[,CFFreq]) Financial function that calculates net present value; the sum of the present values for the cash inflows and outflows. A positive result for npv indicates a profitable investment. InterestRate is the rate by which to discount the cash flows (the cost of money) over one period. CF0 is the initial cash flow at time 0; it must be a real number. CFList is a list of cash flow amounts after the initial cash flow CF0. CFFreq is a list in which each element specifies the frequency of occurrence for a grouped (consecutive) cash flow amount, which is the corresponding element of CFList. The default is 1; if you enter values, they must be positive integers < 10,000. |
|
|
Catalog > |
|
|
nSolve(Equation,Var[=Guess]) ⇒ number or error_string nSolve(Equation,Var[=Guess],lowBound) ⇒ number or error_string nSolve(Equation,Var[=Guess],lowBound,upBound) ⇒ number or error_string nSolve(Equation,Var[=Guess]) | lowBound≤Var≤upBound ⇒ number or error_string Iteratively searches for one approximate real numeric solution to Equation for its one variable. Specify the variable as: variable
For example, x is valid and so is x=3. |
Note: If there are multiple solutions, you can use a guess to help find a particular solution. |
|
nSolve() attempts to determine either one point where the residual is zero or two relatively close points where the residual has opposite signs and the magnitude of the residual is not excessive. If it cannot achieve this using a modest number of sample points, it returns the string “no solution found.” |
|