In Lesson 11.3 you investigated when the surface area of a can was minimized. In this lesson you will explore the more realistic problem of finding when the amount of material used is minimized.

Cleaning Up

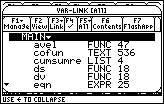
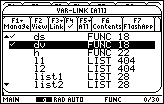
Before you begin this lesson you should delete the functions used in previous lessons to ensure you start with a clean slate, but the commands in the Clean Up menu, such as NewProb, will only delete functions with one-letter names. The following Tech Tip explains how to delete other variables, such as ds.

Deleting Stored Items To delete items, Display the alphabetic listing of stored items by pressing If the Main section is not expanded, highlight it and press to show the list of items stored there. Highlight an item to be deleted Select the highlighted item by pressing You should see a check mark by the selected items. Repeatedly highlight and select items to be deleted Delete the selected items by pressing

Stating the Problem

A can is made from a rectangular piece that forms the lateral surface and two circles cut from square pieces that form the top and bottom. What is the ratio of height to radius if the amount of material used is minimized?

Drawing the Diagrams

The diagrams below illustrate a can of height h and radius r with the top and bottom cut from squares of material.

Although the shaded area is not part of the can, it must be included in the material used.

11.4.1 Use your TI-89 and the methods of Lesson 11.2 and Lesson 11.3 to find the ratio of height to radius that minimizes the amount of material used. Give exact and approximate values. Click here for the answer.

Demonstrating the Solution

Click here to download the script can.89t, which demonstrates the solution to the problem.

Click here to get information about how to obtain the needed cable and to review the procedure to transfer the program from your computer to your calculator.

• Run the script