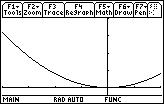
Critical point(s): x = 0

Local and absolute minimum of 0 at x = 0.

Local maximum of 16 at x = –4 and 4 at x = 2.

Absolute maximum of 16 at x = –4.

1. 
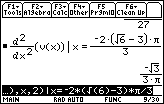
2. The zero of the derivative occurs at x 3.43653.
3. 

When x 3.43653, the surface area is approximately 222.608.

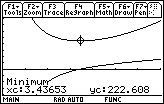
4. The minimum surface area of approximately 222.608 square units occurs when the radius of the can is approximately 3.43653 units.
5. The x-value at the minimum of the function is the same as the zero of the function's derivative. The positive second derivative indicates that the x-value represents a local minimum value.

Thus,

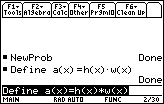
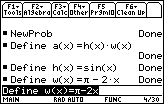
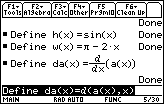
The area function a(x) is continuous on [0, /2] and its derivative is defined for all x in this interval as we can see from the formula in the answer to Self Test Question 4. Thus, the only critical point of a(x) is the zero of the derivative of the area function. Also a(0) = a( /2) = 0. In the two figures below we see that the second derivative is negative at the zero x 0.710463 of the first derivative, so the graph of the area function is concave downward and there is a local maximum at the point (0.710463, 1.12219). This local maximum ( 1.12219) must also be the absolute maximum of a(x) on [0, /2].

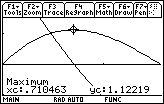
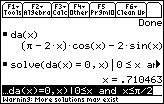
The maximum area of approximately 1.12219 occurs where the first derivative is zero, x 0.710463. The area function is zero at the endpoints of its domain and its first derivative is defined on the entire interval, so this is an absolute maximum.