In this lesson you will explore finding the maximum volume of a cone that is made by removing a sector from a circular piece of paper. You will write a function for volume in terms of the length of the arc that is removed and use the zeros of the function's derivative to identify values that will be used to find maximum volume.

Before beginning the problem start with a clean slate.

• Execute NewProb from the F6:Clean Up menu

Stating the Problem

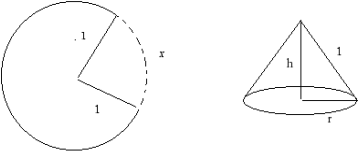
Removing a sector from a circular piece of paper of radius one unit and fastening together the remaining seams creates a cone. Find the length of the arc of the sector that will result in the cone of maximum volume. What is the maximum volume? Solve the problem analytically and support it graphically.

Drawing the Diagrams

Diagrams that represent the problem are shown below. The one on the left depicts the circular piece of paper with a sector removed and the one on the right illustrates the completed cone.

Defining Volume as a Function of r and h

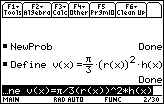
The quantity to be maximized is the volume of the cone. If the cone's height is h and r is its radius, its volume is given by .

Letting x represent the length of the arc removed, the variables r and h can each be written as a function of x. That is, volume can be written as .

• Define v(x)= /3*(r(x))^2*h(x)

Defining r and h as Functions of x

The circumference of the base of the cone is equal to the arc of the circle remaining after the sector is removed. The circumference of the circular base of the cone can be written in two ways:

The formula for finding the circumference of the circular base of a cone of radius r is c = 2 r.

The circumference of the circular piece of paper less the length of the removed arc is c = 2 – x.

Because 2 r and 2 – x represent the same quantity, 2 r = 2 – x .

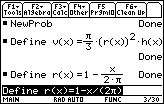
Solving the equation for r gives , which expresses r as a function of x.

• Define r(x)=1-x/(2 )

The equation h ² + r ² = 1, which is obtained from the Pythagorean theorem, can be used to define h as a function of r. Because h can be written as a function of r and r is a function of x, h can be written as a function of .

• Define

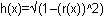
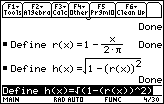
Volume was originally defined as a function of r and h. Because r is a function of x and h is a function of r, volume is now defined as a function of x.

Taking the Derivative of Volume with Respect to x

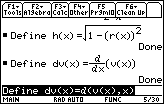
Store the derivative of the volume function, v, in a new function named dv.

• Define dv(x)=d(v(x),x)

Be sure to use the alpha key for "d" in "dv" and the derivative key for "d" in the derivative command.

Finding the Domain of the Problem

Because the length of an arc that can be removed is greater than or equal to 0 and less than or equal to the circle's circumference, 2 , the domain of the problem is 0 x 2 .

Finding Extreme Values of the Function v on [0, 2 ]

Any extreme value of the function must occur at a critical point or an endpoint. These values are :

1. all zeros of the first derivative,
2. all values where the first derivative is undefined, and
3. the endpoints 0 and 2 of the function's domain.

Once all critical points are found, the function may be evaluated at those values and at the endpoints to determine where the maximum occurs.

Finding the Zeros of the Derivative

We need only find the zeros of the derivative function dv on the interior of the interval : 0 < x < 2 .

• Enter solve (dv(x)=0,x)| 0<x and x<2

  The symbol "<" is found above 0 and the logical operator "and" is in the catalog.

• Display the exact value by pressing
• Display a decimal approximation by pressing

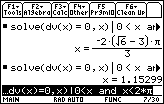
The derivative is zero when , which is a critical point.

Endpoint Values

Evaluate v(0) and v(2 ) to see v(0) = v(2 ) = 0.

Finding when the First Derivative is Undefined

• Compute dv(x).
  The first derivative is defined everywhere in the interval 0 < x 2 , and is undefined at x = 0 as shown below.

You will need to scroll to the right to see that

The derivative dv(x) is undefined at x = 0, which is not a critical point because it is an endpoint.

Finding the Volume at the Critical Point

Find the volume at the critical point .

• Enter

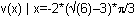
  The last part of this command, " 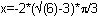" can be pasted from the History Area.

 

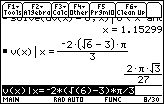
The result shown, , is the exact volume when the length of the removed arc is .

11.2.1 Find a decimal approximation of the volume when . Click here for the answer.

Conclusion

The value at the endpoints is 0, there is only one critical point and the function is positive there. Therefore, the maximum volume is and it occurs when .

Graphing the Function and its Derivative

The maximum volume and its relationship to the corresponding zero of its first derivative can be illustrated by viewing the graphs of the volume function and its derivative.

• Set y1 = v(x)
• Set y2 = dv(x)
• Display the graphs in a [0, 2 ] x [-0.1, 0.5] window with xscl = 1 and yscl = 0.1
• Find the zero of the derivative by using the Zero feature in the F5:Math menu
• Find the maximum value of the function by using the Maximum feature in the F5:Math menu

 

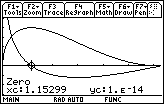
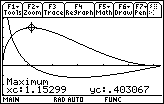
The zero of the derivative corresponds to the x-value at the volume's maximum point.

The length of the removed arc that maximizes the volume is approximately 1.15299 units and the maximum volume is approximately 0.403067 cubic units.

11.2.2 Use the 2nd-derivative test to show that v has a local maximum value at the critical point found above.

Click here for the answer.

Increasing Graphing Speed You may have noticed the TI-89 took a long time to graph y2 = dv(x). You can increase the speed by using the derivative command to compute the derivative of v on the home screen and pasting it into y2.