A rectangle is to be inscribed under the graph of f(x) = sin x in the first quadrant on the interval [0, ], as shown below.

The following questions reflect the procedure used to find the rectangle described above that has maximum area.

Before you begin, execute NewProb to clear stored items.

1. The area of a rectangle is A = hw, where h and w are the height and width of the rectangle, respectively. Assume that h and w are both functions of x and define an area function on your TI-89.
2. Define the height as a function of x.
3. Define the width as a function of x. (Hint: Use the symmetry of the graph.)
4. Define the derivative of the area function and find a formula for it.
5. Find the zeros of the derivative on the interval 0 x
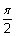
6. Verify that the critical point found in Question 5 produces the absolute maximum of the area function and find the maximum area of the rectangle.
7. Graph the area function and its derivative. Describe the correspondence between the derivative and the maximum of the function.

Click here to check your answers.