Du kan utföra statistiska beräkningar för att analysera data. Följande exempel anpassar den linjära regressionsmodellen y=mx+b till de två listorna i kolumn A och B.

1.

På menyn Statistik, välj Statistisk beräkning> och sedan Linjär regression (mx+b) för att välja regressionsmodellen.

Dialogrutan Linjär regression (mx+b) öppnas.

2.

Ange a[] som kolumn för X-listan.

3.

Ange b[] som kolumn för Y-listan.

4.

För att lagra regressionsekvationen i en angiven variabel ersätter du Spara RegEqn i med namnet på variabeln.

5.

Ange c[] som kolumn för första resultatet.

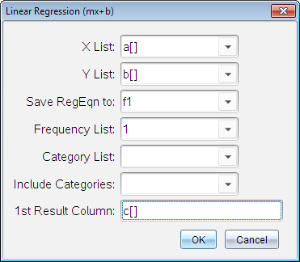
6.

Klicka på OK.

Listor och kalkylblad infogar två kolumner: en innehåller namnen på resultaten och en innehåller motsvarande värden.

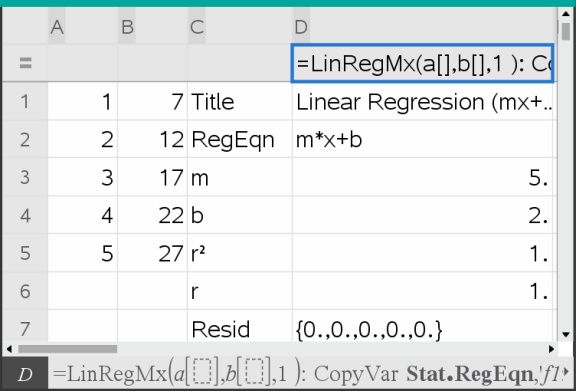
Obs: Resultaten är länkade till dina källdata. Om du t.ex. ändrar ett värde i kolumn A uppdateras regressionsekvationen automatiskt.

 

Listor och kalkylblad lagrar statistiska resultat med ett variabelgruppnamn med formatet stat.nnn, där nnn är resultatnamnet (till exempel stat.RegEqn eller stat.Resid). Användningen av standardnamn på variabler gör det enklare att identifiera och använda de statistiska variablerna senare. Om du vill använda en anpassad variabelgrupp i stället för standardnamnet kan du redigera formeln i kolumnformelcellen.

Du kan använda följande formel för att lagra resultaten i variabelgruppen MystatsB.

=LinRegMx(a[],b[],1 ): CopyVar Stat., MystatsB.

Du kan senare visa resultaten genom att mata in följande formel i applikationen Räknare eller i en annan kolumn i applikationen Listor och kalkylblad:

MiystatsB.resultat

 

I menynStatistiska beräkningar kan du välja från de beräkningar som beskrivs nedan. Se handboken för TI-Nspire™ för mer information.

Envariabelstatistik (OneVar)

Analyserar data med en uppmätt variabel. Du kan specificera en valfri frekvenslista. De statistiska data som erhålls med denna analysteknik är:

•

Medelvärdet för ett urval, x

•

Summan av data, Gx

•

Kvadratsumman, Gx2

•

Standardavvikelse för urvalet, sx

•

Standardavvikelse för populationen, sx

•

Urvalsstorlek, n

•

X-min

•

Undre kvartil, Q1

•

Median

•

Övre kvartil, Q3

•

X-max

•

Summan av kvadratiska avvikelser, SSx = G(x Nx)2

Tvåvariabelstatistik (TwoVar)

Analys av parvisa data. Lista 1 är den oberoende variabeln. Lista 2 är den beroende variabeln. Du kan specificera en valfri frekvenslista. De statistiska data som erhålls med denna analysteknik är:

För varje lista:

•

Medelvärdet för ett urval, x eller y

•

Summan av data, Gx eller Gy

•

Kvadratsumman, Gx2 eller Gy2

•

Standardavvikelse för urvalet, sx = sn-1x eller sy = sn-1y

•

Standardavvikelse för populationen, sx = snx eller sy = sny

•

X-min eller Y-min

•

Undre kvartil, Q1X eller Q1Y

•

Median

•

Övre kvartil, Q3X eller Q3Y

•

X-max eller Y-max

•

Summan av kvadratiska avvikelser, SSx = G(x Nx)2 eller SSy = G(y Ny)2

Övriga data:

•

Urvalsstorlek för varje datauppsättning, n

•

Gxy

•

Korrelationskoefficient, R.

Linjär regression (mx+b) (LinRegMx)

Anpassar modellekvationen y=ax+b efter data med minsta kvadrat-metoden. Den visar värden för m (lutning) och b (skärning med y-axeln).

Linjär regression (a+bx) (LinRegBx)

Anpassar modellekvationen y=a+bx efter data med minsta kvadrat-metoden. Den visar värden för a (skärning med y-axeln), b (lutning), r2 och r.

Median–Median-linje (MedMed)

Anpassar modellekvationen y=mx+b efter data med tekniken median-median-linje (fast linje) och beräknar summapunkterna x1, y1, x2, y2, x3 och y3. Median–median-linje visar värden för m (lutning) och b (skärning med y-axeln).

Kvadratisk regression (QuadReg)

Anpassar andragradspolynomet y=ax2+bx+c efter data. Den visar värden för a, b, c, och R2. För tre datapunkter är ekvationen en polynomanpassning. För fyra eller fler punkter är den en polynomregression. Minst tre datapunkter krävs.

Kubisk regression (CubicReg)

Anpassar tredjegradspolynomet y=ax3+bx2+cx+d efter data. Den visar värden för a, b, c, d, och R2. För fyra datapunkter är ekvationen en polynomanpassning. För fem eller fler punkter är den en polynomregression. Minst fyra datapunkter krävs.

Kvartär regression (QuartReg)

Anpassar fjärdegradspolynomet y=ax4+bx3+cx2+dx+e efter data. Den visar värden för a, b, c, d, e, och R2. För fem datapunkter är ekvationen en polynomanpassning; För sex eller fler punkter är den en polynomregression. Minst fem datapunkter krävs.

Potensregression (PowerReg)

Anpassar modellekvationen y=axb efter data med minsta kvadrat-metoden och de transformerade värdena ln(x) och ln(y). Den visar värden för a, b, r2 och r.

Exponentiell regression (ExpReg)

Anpassar modellekvationen y=abx efter data med minsta kvadrat-metoden och de transformerade värdena x och ln(y). Den visar värden för a, b, r2 och r.

Logaritmisk regression (LogReg)

Anpassar modellekvationen y=a+b ln(x) efter data med minsta kvadrat-metoden och de transformerade värdena ln(x) och y. Den visar värden för a, b, r2 och r.

Sinusregression (SinReg)

Anpassar modellekvationen y=a sin(bx+c)+d efter data med en iterativ minsta kvadrat-metod. Den visar värden för a, b, c, och d. Minst fyra datapunkter krävs Minst två datapunkter per cykel krävs för att undvika bristfälliga frekvensuppskattningar.

Obs: Resultatet av SinReg är alltid i radianer, oavsett inställningen av Radian/Grad-läget.

Logistisk regression (d=0) (Logistic)

Anpassar modellekvationen y=c/(1+a*e-bx) efter data med en iterativ minsta kvadrat-metod. Den visar värden för a, b och c.

Logistisk regression (dƒ0) (LogisticD)

Anpassar modellekvationen y=c(1+a*e(-bx))+d efter data med en iterativ minsta kvadrat-metod. Den visar värden för a, b, c och d.

Multipel linjär regression (MultReg)

Beräknar den multipla linjära regressionen i lista Y på listorna X1, X2, …, X10.