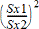Statistiska tester som stöds
Hypotestester är tillgängliga från applikationen Listor och kalkylblad. För mer information om dessa funktioner kan du se referensguiden för TI-Nspire™.
Vissa guider för Stat Tests visar en kryssruta för Rita. Som förval är rutan inte markerad. Om du markerar denna kryssruta skapas ett arbetsområde i Data och statistik på sidan och resultaten plottas i det arbetsområdet.
z-test (zTest)
Utför ett hypotestest för ett okänt populationsmedelvärde, m, när populationens standardavvikelse, s, är känd. Detta testar nollhypotesen H0: m=m0 mot ett av nedanstående alternativ
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Detta test används för stora populationer som är normalfördelade. Standardavvikelsen måste vara känd.
Detta test kan användas för att bestämma om skillnaden mellan medelvärdet för ett urval och medelvärdet för en population är statistiskt signifikant när du vet den sanna avvikelsen för en population.
t-test (tTest)
Utför ett hypotestest för ett okänt populationsmedelvärde, m, när populationens standardavvikelse, s, är okänd. Detta testar nollhypotesen H0: m=m0 mot ett av nedanstående alternativ
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Detta test liknar ett z-test, men det används när populationen är liten och normalfördelad. Testet används oftare än z-testet eftersom små urvalspopulationer är vanligare än stora inom statistik.
Som exempel kan detta test användas för att bestämma om två normalfördelade populationer har samma medelvärden, eller när du vill bestämma om medelvärdet för ett urval skiljer sig signifikant från medelvärdet för en population och populationens standardavvikelse är okänd.
2-sampel z-test (zTest_2Samp)
Testar överensstämmelsen mellan medelvärdena för två populationer (m1 och m2) baserat på oberoende urval när båda populationernas standardavvikelser (s1 och s2) är kända. Nollhypotesen H0: m1=m2 testas mot ett av nedanstående alternativ.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
2-sampel t-test (tTest_2Samp)
Testar överensstämmelsen mellan medelvärdena för två populationer (m1 och m2) baserat på oberoende urval när ingen av populationernas standardavvikelser (s1 eller s2) är känd. Nollhypotesen H0: m1=m2 testas mot ett av nedanstående alternativ.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
1-prop z-test (zTest_1Prop)
Beräknar ett test för en okänd proportion av lyckade försök (prop). Som indata används antalet lyckade försök i urvalet x och antalet observationer i urvalet n. 1-prop z-test testar nollhypotesen H0: prop=p0 mot ett av nedanstående alternativ.
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
Detta test kan användas för att bestämma om sannolikheten för att lyckas i ett försök som observerats i ett urval signifikant skiljer sig från sannolikheten för att lyckas i ett försök i populationen, eller om skillnaden beror på samplingsfel, avvikelse eller andra faktorer.
2-prop z-test (zTest_2Prop)
Beräknar ett test för att jämföra proportionerna av lyckade försök (p1 och p2) i två populationer. Som indata används antalet lyckade försök i varje urval (x1 och x2) och antalet observationer i varje urval (n1 och n2). 2-prop z-test testar nollhypotesen H0: p1=p2 (med den sammanvägda urvalsproportionen Ç) mot ett av nedanstående alternativ.
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
Detta test kan användas för att bestämma om sannolikheten för att lyckas i två urval är lika.
c2GOF (c2GOF)
Utför ett test för att bekräfta att urvalsdata är från en population som följer en specificerad fördelning. Som exempel kan c2 GOF bekräfta att urvalsdata kommer från en normalfördelning.
c2 2-vägstest (c22way)
Beräknar ett chi-kvadrat-test för associationer i tvåvägstabellen över värden i specificerad Observerad matris. Nollhypotesen H0 för en tvåvägstabell är: ingen association föreligger mellan radvariabler och kolumnvariabler. Den alternativa hypotesen är: variablerna är relaterade.
2-sampel F-test (FTest_2Samp)
Utför ett F--test för att jämföra två normalpopulationers standardavvikelser (s1 och s2). Populationernas medelvärden och standardavvikelser är alla okända. 2-sampel F-test, vilket använder förhållandet mellan urvalsvarianserna Sx12/Sx22, testar nollhypotesen H0: s1=s2 mot ett av nedanstående alternativ.
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
Nedan följer definitionen på 2-sampel F-test.
|
Sx1, Sx2 |
= |
Standardavvikelser hos urval med respektive n1N1 och n2N1 frihetsgrader df. |
|
|
|
F-statistisk = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ) med frihetsgrader df, n1N1 och n2N1 |
|
p |
= |
rapporterat p-värde |
2-sampel F-test för den alternativa hypotesen s1 > s2.
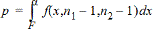
2-sampel F-test för den alternativa hypotesen s1 < s2.
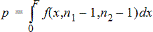
2-sampelF-test för den alternativa hypotesen s1ƒs2. Gränsvärden måste uppfylla följande:
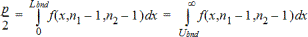
där: [Lbnd,Ubnd]=nedre och övre gränser
F-statistika används som den gräns som ger den minsta integralen. Den återstående gränsen väljs för att uppnå den föregående integralens likhetsförhållande.
Linjär reg t-test (LinRegtTest)
Utför en linjär regressionsanalys på givna data och ett t-test på lutningens värde b samt korrelationskoefficienten r för ekvationen y=a+bx. Det testar nollhypotesen H0: b=0 (ekvivalent, r=0) mot ett av nedanstående alternativ.
| • | Ha: bƒ0 och rƒ0 |
| • | Ha: b<0 och r<0 |
| • | Ha: b>0 och r>0 |
Multipla reg tester (MultRegTest)
Utför en linjär regression på givna data och ger F-teststatistik på linjäritet.
Se referensguiden för TI-Nspire™ för mer information.
ANOVA (ANOVA)
Beräknar en 1-vägs variansanalys för att jämföra medelvärdena hos 2 till 20 populationer. ANOVA-proceduren för att jämföra dessa medelvärden omfattar analys av variationen hos urvalsdata. Nollhypotesen H0: m1=m2=...=mk testas mot alternativet Ha: inte alla m1...mk är lika.
ANOVA-testet är en metod för att bestämma om det finns någon signifikant skillnad mellan grupperna jämfört med skillnaden inom varje grupp.
Detta test kan användas för att bestämma om variationen i data från urval till urval har en statistiskt signifikant effekt på andra faktorer än variationen inom själva datauppsättningarna. Ett exempel: En lådinköpare för ett transportföretag vill utvärdera tre olika lådtillverkare. Han erhåller ett urval av provlådor från alla tre leverantörerna. ANOVA kan hjälpa honom att bestämma om skillnaderna mellan varje urvalsgrupp är signifikant jämfört med skillnaderna inom varje urvalsgrupp.
ANOVA 2-vägs (ANOVA2way)
Beräknar en 2-vägsvariansanalys för att jämföra medelvärdena hos 2 till 20 populationer. En sammanfattning av resultaten lagras i variabeln stat.results.
ANOVA tvåvägs variansanalys undersöker effekterna av två oberoende variabler och bidrar till att bestämma om dessa samverkar med den beroende variabeln. (Om de två oberoende variablerna samverkar kan deras kombinerade effekt additivt vara större eller mindre än effekten av en oberoende variabel.)
Detta test kan användas för att utvärdera skillnader liknande ANOVA-analysen, men med ytterligare en potentiellt inverkande faktor. För att fortsätta med ANOVA-exemplet med transportlådorna: tvåvägsanalysen kan undersöka effekten av lådornas material i de observerade skillnaderna.
Välja en alternativ hypotes (ƒ < >)
Flertalet av verktygen för statistisk inferens för hypotestesterna uppmanar dig att välja en av tre alternativa hypoteser.
| • | Den första är en alternativ hypotes av typ ƒ, t.ex. mƒm0 för z-test. |
| • | Den andra är en alternativ hypotes av typ <, t.ex. m1m2 för m1<m2 för 2-sampel t-test. |
| • | Det tredje är> alternativ hypotes som p1>p2 för 2-prop z-test. |
För att välja en alternativ hypotes, flytta markören till önskat alternativ och tryck sedan på Enter.
Välja alternativet Sammanvägda
sammanvägda (bara2-sampel t-test och 2-sampel t-intervall) specificerar om varianserna för funktionen skall slås samman.
| • | Välj Nejom du inte vill sammnanväga varianserna. Populationsvarianserna kan vara olika. |
| • | Välj Jaom du vill sammanväga varianserna. Populationsvarianserna förutsätts vara lika. |
För att välja alternativet Sammanvägda väljer du Ja i listrutan.