Exempel: Beräkna en fördelning för att passa fördelningsmodellen Normal Pdf.
| 1. | Klicka på kolumnformelcellen (andra cellen ovanifrån räknat) i kolumn A. |
| 2. | Klicka på Statistik - Fördelningar - normal pdf för att välja fördelningsmodellen. |
Dialogrutan Normal Pdf öppnas och visar fält för att skriva in eller välja argumenten för beräkningen.
| 3. | Tryck på Tab för att flytta från fält till fält och ange varje argument. Du kan skriva in värden eller välja dem i listrutan: |
| - | X-värde: Klicka på rullgardinspilen för att välja en lista i problemet och ange x-värdena för beräkningen. |
| - | Medelvärde: Skriv in ett värde för medelvärdet eller klicka på rullgardinspilen och välj en variabel som innehåller medelvärdet. |
| - | Standard Deviation (Standardavvikelse): Skriv in ett värde för standardavvikelsen eller välj en variabel som innehåller standardavvikelsen. |
| 4. | Klicka på kryssrutan Rita för att se fördelningen plottad i Data & Statistik. |
Obs: Ritfunktionen är inte tillgänglig för alla fördelningar.
| 5. | Klicka på OK. |
Listor & kalkylblad infogar två kolumner: en innehåller namnen på resultaten och en innehåller motsvarande värden. Resultaten plottas i Data & Statistik.
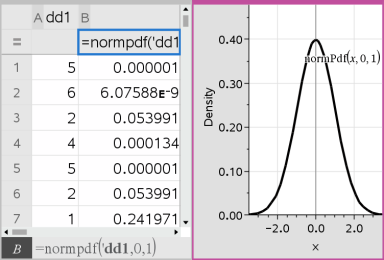
Obs: Resultaten är länkade till dina källdata. Du kan till exempel ändra ett värde i kolumn A, varpå ekvationen uppdateras automatiskt.
Följande fördelningar är tillgängliga från applikationen Listor & Kalkylblad. För mer information om dessa funktioner kan du se referensguiden för TINspire™.
| • | För att erhålla ett enda fördelningsresultat baserat på ett enskilt värde matar du in funktionen i en enskild cell. |
| • | För att erhålla en lista över fördelningsresultat baserat på en lista över värden matar du in funktionen i en kolumnformelcell. I detta fall specificerar du en lista (kolumn) som innehåller värdena. För varje värde på listan ger fördelningen ett motsvarande resultat. |
Obs: För fördelningsfunktioner som stöder plotfunktionen (normPDF, t PDF, χ² Pdf och F Pdf) är alternativet endast tillgängligt om fördelningsfunktionen matas in i en formelcell.
Normal Pdf (normPdf)
Beräknar värdet hos täthetsfunktionen (pdf) för normalfördelningen vid ett specificerat x-värde. De förinställda värdena är medelvärde μ=0 och standardavvikelse σ=1. Täthetsfunktionen (pdf) är:
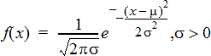
Denna fördelning används för att bestämma sannolikheten för förekomsten av ett visst värde i en normalfördelning. Ritfunktionen är tillgänglig när Normal PDF aktiveras från en formelcell.
När du använder fördelningar från formelcellen måste du välja en giltig lista i listrutan för att undvika oväntade resultat. Om du hämtar den från en cell måste du ange ett tal för x-värdet. Fördelningen ger sannolikheten för att det värde som du angett kommer att inträffa.
Normal Cdf (normCdf)
Beräknar sannolikheten vid en normalfördelning mellan Nedre gräns och Övre gräns för det specificerade medelvärdet μ (förinställning = 0) och standardavvikelsen s (förinställning = 1). Du kan klicka på kryssrutan Rita (Skugga område) för att skugga området mellan den nedre och den övre gränsen. Om de initiala värdena för lowBound och upBound uppdateras fördelningen automatiskt.
Denna fördelning kan användas för att bestämma sannolikheten för förekomsten av ett värde mellan den nedre och den övre gränsen i normalfördelningen. Det är ekvivalent med att söka arean under den angivna normalfördelningskurvan mellan gränserna.
Invers normal (invNorm)
Beräknar värdet av fördelningsfunktionen (kumulativa normalfördelningen) för en given area under normalfördelningskurvan, specificerad av medelvärdet μ och standardavvikelsen s.
Denna fördelning kan användas för att bestämma x-värdet på data i området 0 till x<1 när percentilen är känd.
t Pdf (tPdf)
Beräknar täthetsfunktionen (pdf) för t-fördelning vid ett specificerat x-värde. df (frihetsgrader) måste vara >0. Täthetsfunktionen (pdf) är:
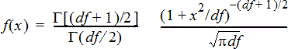
Denna fördelning kan användas för att bestämma sannolikheten för förekomsten av ett värde när populationens standardavvikelse är okänd och urvalet är litet. Ritfunktionen är tillgänglig när t Pdf aktiveras från en formelcell.
t Cdf (tCdf)
Beräknar sannolikheten för Student-t-fördelning mellan Nedre gräns och Övre gräns för specificerade df (frihetsgrader). Du kan klicka i kryssrutan Rita (Skugga område) för att skugga området mellan gränslinjerna. Om de initiala värdena för lowBound och upBound uppdateras fördelningen automatiskt.
Denna fördelning kan användas för att bestämma sannolikheten för förekomsten av ett värde inom ett intervall definierat av den nedre och den övre gränsen för en normalfördelad population när populationens standardavvikelse är okänd.
invers t (invt)
Beräknar den inversa kumulativa sannolikhetsfunktionen för t-fördelningen specificerad av frihetsgrader (df) för en given area under kurvan.
Denna fördelning kan användas för att bestämma sannolikheten för en förekomst av data i området 0 till x<1. Denna funktion används när populationens medelvärde och/eller populationens standardavvikelse är okänd(a).
c2 Pdf (c2 Pdf())
Beräknar täthetsfunktionen (pdf) för c2-fördelning (chi-kvadrat) vid ett specificerat x-värde. df (frihetsgrader) måste vara ett heltal >0. Täthetsfunktionen (pdf) är:
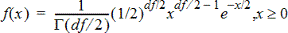
Denna fördelning kan användas för att bestämma sannolikheten för förekomsten av ett givet värde från en population med en c2 -fördelning. Ritfunktionen är tillgänglig när c2 Pdf aktiveras från en formelcell.
c2 Cdf (c2 Cdf())
Beräknar sannolikheten för c2-fördelningen (chi-kvadrat) mellan nedre gräns och övre gräns för specificerade df (frihetsgrader). Du kan klicka på kryssrutan Rita (Skugga område) för att skugga området mellan den nedre och den övre gränsen. Om de initiala värdena för lowBound och upBound ändras uppdateras fördelningen automatiskt.
Denna fördelning kan användas för att bestämma sannolikheten för förekomsten av ett värde inom givna gränser hos en population med en c2 -fördelning.
F Pdf (F Pdf())
Beräknar täthetsfunktionen (pdf) för F-fördelningen vid ett specificerat x-värde. Täljare df (frihetsgrader) och nämnare df >måste vara heltal >0. Täthetsfunktionen (pdf) är:
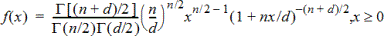
|
Där |
n = täljare, frihetsgrader |
Denna fördelning kan användas för att bestämma sannolikheten för att två urval har samma varians. Ritfunktionen är tillgänglig när F Pdf aktiveras från en formelcell.
F Cdf (F Cdf())
Beräknar sannolikheten för F-fördelning mellan Nedre gräns och Övre gräns för specificerade dfNumer (frihetsgrader) och dfDenom. Du kan klicka på kryssrutan Rita (Skugga område) för att skugga området mellan den nedre och den övre gränsen. Om de initiala värdena för lowBound och upBound ändras uppdateras fördelningen automatiskt.
Denna fördelning kan användas för att bestämma sannolikheten för att en enstaka observation faller inom området mellan den nedre gränsen och den övre gränsen.
Binomial Pdf (binomPdf())
Beräknar en sannolikhet vid x för den diskreta binomialfördelningen med specificerad numtrials (antal försök) och sannolikhet för att lyckas (p) vid varje försök. Parametern x kan vara ett heltal eller en lista över heltal. 0{p{1 måste vara sann. numtrials måste vara ett heltal >0. Om du inte specificerar x erhåller du en lista på sannolikheter från 0 till numtrials. Täthetsfunktionen (pdf) är:
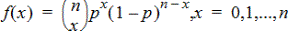
där n = antal försök
Denna fördelning kan användas för att bestämma sannolikheten för att lyckas/misslyckas vid n försök. Du kan exempelvis använda denna fördelning för att förutspå sannolikheten för att få tre krona vid fem försök när du singlar slant.
Binomial Cdf (binomCdf())
Beräknar en kumulativ sannolikhet för den diskreta binomialfördelningen med n antal försök och sannolikheten p för att lyckas vid varje försök.
Denna fördelning kan användas för att bestämma sannolikheten för att lyckas vid ett försök innan alla försök har gjorts. Om exempelvis krona betyder att lyckas och du singlar slant 10 gånger kan denna fördelning beräkna sannolikheten för att få krona (lyckas) minst en gång av de 10 kasten.
Invers binomial (invBinom())
Baserat på antalet försök (NumTrials) och sannolikheten för önskat utfall av varje försök (Prob) ger denna funktion det minimala antalet lyckade utfall, k, så att den kumulativa sannolikheten,k, är större än eller lika med den givna kumulativa sannolikheten (CumulativeProb).
Invers binomial med hänsyn till N (invBinomN())
Baserat på sannolikheten för lyckat utfall i varje försök (Prob) och antalet lyckade försök (NumSuccess) beräknar funktionen det minsta antalet försök, N, så att den kumulativa sannolikheten för x lyckade utfall är mindre eller lika med den givna kumulativ sannolikheten (CumulativeProb).
Poisson Pdf (poissPdf())
Beräknar en sannolikhet vid x för den diskreta Poisson-fördelningen med det specificerade medelvärdet μ, vilket måste vara ett reellt tal >0. x kan vara ett heltal eller en lista av heltal. Täthetsfunktionen (pdf) är:
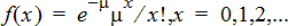
Denna fördelning kan användas för att bestämma sannolikheten för att lyckas ett visst antal gånger innan en försöksomgång börjar. Du kan till exempel använda denna beräkning för att förutspå hur många gånger resultatet skulle bli krona om du singlar slant åtta gånger.
Poisson Cdf (poissCdf())
Beräknar en kumulativ sannolikhet för den diskreta Poisson-fördelningen med det specificerade medelvärdet x.
Denna fördelning kan användas för att bestämma sannolikheten för att lyckas ett visst antal gånger mellan den övre och den nedre gränsen under en försöksomgång. Du kan till exempel använda denna beräkning när du singlar slant för att förutspå hur många gånger resultatet blir "krona" mellan kast nummer 3 och 8.
Geometrisk Pdf (geomPdf())
Beräknar en sannolikhet vid x, vid vilket försök i försöksomgången som man lyckas första gången, för den diskreta geometriska fördelningen med den specificerade sannolikheten p för att lyckas. 0{p{1 måste vara sann. xkan vara ett heltal eller en lista över heltal. Täthetsfunktionen (pdf) är:
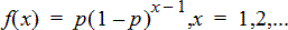
Denna fördelning kan användas för att bestämma det mest sannolika antalet försök som krävs innan försöket lyckas. Du kan till exempel använda denna beräkning för att förutspå hur många gånger ett mynt måste singlas innan resultatet blir krona.
Geometrisk Cdf (geomCdf())
Beräknar en kumulativ geometrisk sannolikhet från Nedre gräns till Övre gräns med den specificerade sannolikheten p för att lyckas.
Denna fördelning kan användas för att bestämma sannolikheten vid det första lyckade försöket under försök 1 till och med n. Du kan exempelvis använda denna beräkning för att bestämma sannolikheten för att resultatet blir krona vid försök #1, #2, #3, ..., #n.