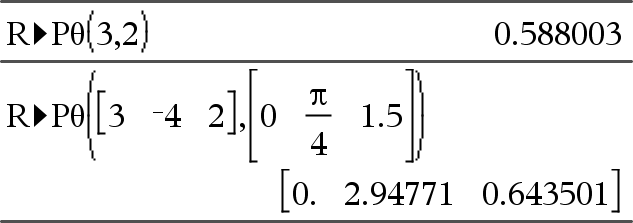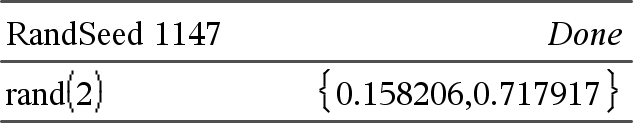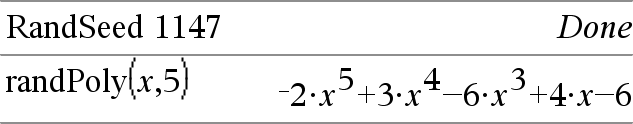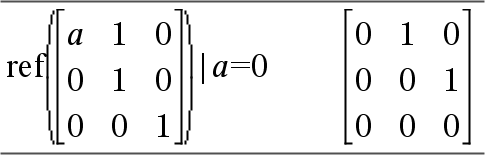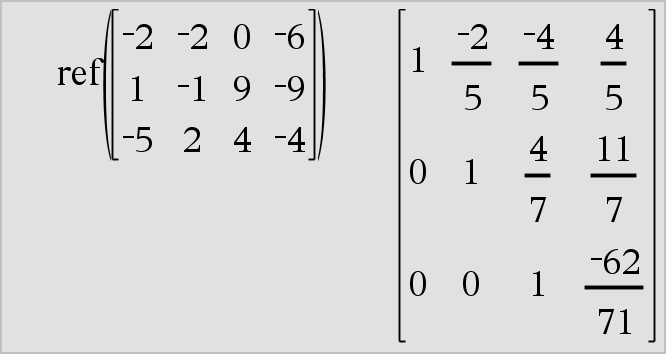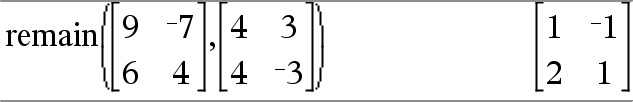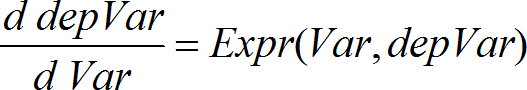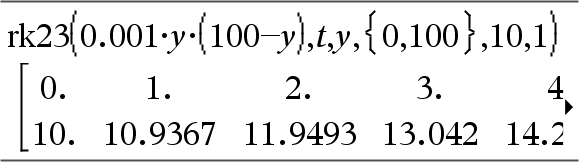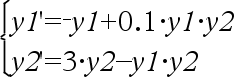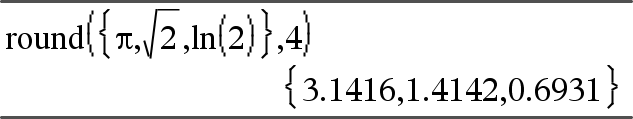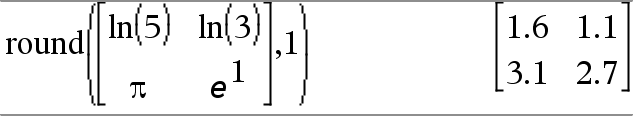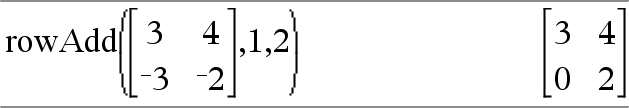R

R►Pθ()

Catalogo >


R►Pθ (valoreX, valoreY) ⇒ valore
R►Pθ (listaX, listaY) ⇒ lista
R►Pθ (matriceX, matriceY) ⇒ matrice

Restituisce la coordinata θ equivalente della
coppia di argomenti (x,y).

Nota: conformemente alla modalità di misurazione degli angoli impostata, il risultato è in gradi, gradi centesimali o radianti.

Nota: è possibile inserire questa funzione dalla tastiera del computer digitando R@>Ptheta(...).

In modalità angolo in gradi:


In modalità angolo in gradi centesimali:


In modalità angolo in radianti:

R►Pr()

Catalogo >


R►Pr (valoreX, valoreY) ⇒ valore
R►Pr (listaX, listaY) ⇒ lista
R►Pr (matriceX, matriceY) ⇒ matrice

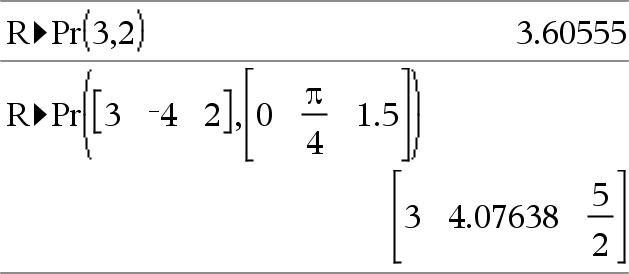
Restituisce la coordinata r equivalente alla coppia di argomenti (x,y).

Nota: è possibile inserire questa funzione dalla tastiera del computer digitando R@>Pr(...).

In modalità angolo in radianti:

►Rad

Catalogo >

Valore1►Rad ⇒ valore

Converte l’argomento in una misura d’angolo in radianti.

Nota: è possibile inserire questo operatore dalla tastiera del computer digitando @>Rad.

In modalità angolo in gradi:


In modalità angolo in gradi centesimali:

rand() (Numero casuale)

Catalogo >

rand() ⇒ espressione
rand(numTentativi) ⇒ lista

rand() restituisce un numero casuale compreso tra 0 e 1.

rand(numTentativi) restituisce una lista contenente numTentativi valori casuali compresi tra 0 e 1.

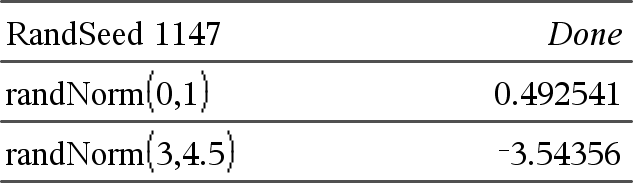
Imposta il seme dei numeri casuale.

randBin() (Numero casuale da distribuzione binomiale)

Catalogo >

randBin(n, p) ⇒ espressione
randBin(n, p, numTentativi) ⇒ lista

randBin(n, p) restituisce un numero reale casuale da una distribuzione binomiale specificata.

randBin(n, p, numTentativi) restituisce una lista contenente numTentativi numeri reali casuali da una distribuzione binomiale specificata.

randInt() (Intero casuale)

Catalogo >

randInt(estremoInf,estremoSup) ⇒ espressione
randInt(estremoInf,estremoSup ,numTentativi)⇒ lista

randInt(estremoInf,estremoSup) restituisce un intero casuale all’interno dell’intervallo specificato dai numeri interi estremoInf e estremoSup.

randInt(estremoInf,estremoSup,numTentativi) restituisce un elenco contenente numTentativi interi casuali all’interno dell’intervallo specificato.

randMat() (Matrice casuale)

Catalogo >

randMat(numRighe, numColonne) ⇒ matrice

Restituisce una matrice di numeri interi compresi tra -9 e 9 della dimensione specificata.

Entrambi gli argomenti devono potere essere semplificati in numeri interi.

Nota: i valori di questa matrice cambiano ogni volta che si preme ·.

randNorm() (Normale casuale)

Catalogo >

randNorm(μ, σ) ⇒ espressione
randNorm(μ, σ, numTentativi) ⇒ lista

randNorm(μ, σ) restituisce un numero decimale dalla distribuzione normale specificata. Può essere qualsiasi numero reale, anche se con maggiore probabilità sarà compreso nell’intervallo [μ−3•σ, μ+3•σ].

randNorm(μ, σ, numTentativi) restituisce una lista contenente numTentativi valori decimali dalla distribuzione normale specificata.

randPoly() (Polinomio casuale)

Catalogo >

randPoly(Var, Ordine) ⇒ espressione

Restituisce un polinomio in Var dell’Ordine specificato. I coefficienti sono interi casuali compresi tra −9 e 9. Il primo coefficiente non può essere zero.

Ordine deve essere tra 0 e 99.

randSamp() (Campione casuale)

Catalogo >

randSamp(Lista,numTentativi[,noSostituzione]) ⇒ lista

Restituisce una lista contenente un campione casuale di numTentativi da Lista con l’opzione di sostituire il campione (noSostituzione=0) o meno (noSostituzione=1). L’impostazione predefinita prevede la sostituzione del campione.

RandSeed (Seme numero casuale)

Catalogo >

RandSeed Numero

Se Numero = 0, imposta i semi ai valori predefiniti per il generatore di numeri casuali. Se Numero ≠ 0, viene utilizzato per generare due semi, memorizzati nelle variabili di sistema seed1 e seed2.

real() (Reale)

Catalogo >

real(Valore1) ⇒ valore

Restituisce la parte reale dell’argomento.

real(Lista1) ⇒ lista

Restituisce le parti reali di tutti gli elementi.

real(Matrice1) ⇒ matrice

Restituisce le parti reali di tutti gli elementi.

►Rect

Catalogo >

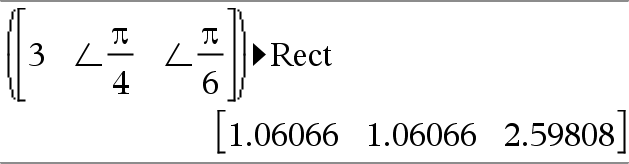
Vettore ►Rect

Nota: è possibile inserire questo operatore dalla tastiera del computer digitando @>Rect.

Visualizza Vettore nella forma rettangolare [x, y, z]. Le dimensioni del vettore devono essere 2 o 3 e il vettore può essere una riga o una colonna.

Nota: ►Rect è un’istruzione del formato di visualizzazione, non una funzione di conversione. Tale istruzione può essere impiegata solo alla fine di una riga di introduzione e non aggiorna ans.

Nota: Vedere anche ►Polar, qui.

valoreComplesso ►Rect

Visualizza valoreComplesso nella forma rettangolare a+bi. valoreComplesso può avere una forma complessa qualsiasi. Tuttavia una voce reiθ causa un errore nella modalità di misurazione degli angoli in gradi.

Nota: è necessario usare le parentesi per un inserimento polare (r∠θ).

In modalità angolo in radianti:


In modalità angolo in gradi centesimali:


In modalità angolo in gradi:

Nota: per inserire ∠ dalla tastiera, selezionarlo nell’elenco dei simboli del Catalogo.

ref() (Forma a scalini per righe)

Catalogo >

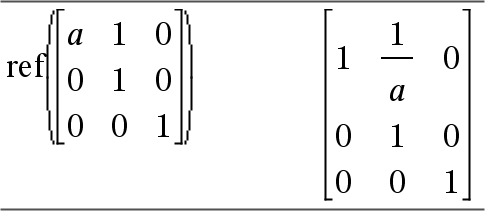
ref(Matrice1[, Tol]) ⇒ matrice

Restituisce la forma a scalini per righe di Matrice1.

In alternativa, un elemento qualsiasi della matrice viene considerato zero se il suo valore assoluto è minore di Tol. Tale tolleranza viene utilizzata solo se la matrice contiene elementi a virgola mobile e non contiene variabili simboliche alle quali non sia stato assegnato un valore. In caso contrario, Tol viene ignorato.

• Se si usa /· oppure se si imposta la modalità Auto o Approssimato su Approssimato, i calcoli saranno eseguiti in virgola mobile.
• Se Tol viene omesso o non è utilizzato, la tolleranza predefinita viene calcolata come:
5E−14 •max(dim(Matrice1)) •rowNorm(Matrice1)

Evitare elementi indefiniti in Matrice1. Possono produrre risultati imprevisti.

Ad esempio, se a è indefinito nella seguente espressione, viene visualizzato un messaggio di avvertenza e il risultato viene mostrato come:

Il messaggio di avvertenza appare perché l’elemento generalizzato 1/a non è valido per a=0.

È possibile evitare questa situazione memorizzando in anticipo un valore in a oppure utilizzando l’operatore di vincolo (“|”), come mostrato nell’esempio che segue.

Nota: vedere anche rref(), here.

 

RefreshProbeVars

Catalogo >

RefreshProbeVars

Permette di accedere ai dati di tutti i sensori collegati in un programma TI-Basic.

Valore di varStato

Stato

varStato=0

Normale (continuare l’esecuzione del programma)

varStato=1

L’applicazione Vernier DataQuest™ è in modalità di raccolta dati.

Nota: affinché questo comando funzioni, l’applicazione Vernier DataQuest™ deve essere in modalità misura.

varStato=2

L’applicazione Vernier DataQuest™ non è stata avviata.

varStato=3

L’applicazione Vernier DataQuest™ è stata avviata, ma non sono presenti sensori collegati.

Esempio

Define temp()=

Prgm

© Verificare se il sistema è pronto

RefreshProbeVars stato

If stato=0 Then

Disp “pronto”

Per n,1,50

RefreshProbeVars stato

temperatura:=meter.temperatura

Disp "Temperatura: ”,temperatura

If temperatura>30 Then

Disp “Caldo eccessivo”

EndIf

© Attendere 1 secondo tra i campioni

Wait 1

EndFor

Else

Disp “Non pronto. Riprovare più tardi”

EndIf

EndPrgm

 

Nota: Può essere utilizzato anche con l’hub di TI-Innovator™.

 

remain() (Resto)

Catalogo >


remain(Valore1, Valore2) ⇒ valore
remain(Lista1, Lista2) ⇒ lista
remain(Matrice1, Matrice2) ⇒ matrice

Restituisce il resto del primo argomento rispetto al secondo argomento, come definito dalle identità:

remain(x,0)   x
remain(x,y)   x−y•iPart(x/y)

Si noti che, di conseguenza remain(−x,y) − remain(x,y). Il risultato può essere zero oppure può avere lo stesso segno del primo argomento.

Nota: vedere anche mod(), qui.

Request

Catalogo >

Request stringaPrompt, var[, FlagDispl [, varStato]]

Request promptString, funz(arg1, ...argn)  [, FlagDisp [, statusVar]]

Istruzione di programmazione: Sospende il programma e visualizza una finestra di dialogo contenente il messaggio stringaPrompt e un riquadro di testo per la risposta dell’utente.

Dopo che l’utente ha digitato una risposta e ha fatto clic su OK, il contenuto del riquadro di testo viene assegnato alla variabile var.

Se l’utente fa clic su Cancel (Annulla), il programma procede senza accettare input. Il programma utilizza il precedente valore di var se var è già stata definita.

L’argomento opzionale FlagDispl può essere qualsiasi espressione.

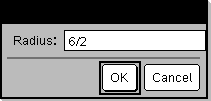
• Se FlagDispl viene omesso o dà come risultato 1, la richiesta e la risposta da parte dell’utente vengono visualizzate nella cronologia della calcolatrice.
• Se FlagDispl dà come risultato 0, la richiesta e la risposta non vengono visualizzate nella cronologia.

Definire un programma:

Define request_demo()=Prgm
    Request “Radius: ”,r
    Disp “Area = “,pi*r2
EndPrgm

 

Eseguire il programma e digitare una risposta:

request_demo()

Risultato dopo aver selezionato OK:

Semiretta: 6/2
Area = 28.2743

L’argomento varStato opzionale offre al programma la possibilità di determinare la modalità di uscita dell’utente dalla finestra di dialogo. Notare che varStato richiede l’argomento FlagDispl.

• Se l’utente ha fatto clic su OK o ha premuto Invio oppure Ctrl+Invio, la variabile varStato viene impostata sul valore 1.
• Altrimenti, la variabile varStato viene impostata sul valore 0.

L’argomento funz() consente a un programma di memorizzare la risposta dell’utente come una definizione di funzione. Questa sintassi opera come se l’utente avesse eseguito il comando:

     Define funz(arg1, ...argn) = risposta utente

Il programma può quindi usare la funzione definita funz(). La stringaPrompt dovrebbe portare l’utente ad inserire una risposta utente appropriata che completi la definizione di funzione.

Nota: è possibile utilizzare il comando Request all’interno di un programma definito dall’utente, ma non di una funzione.

Per arrestare un programma che contiene un comando Request in un loop infinito:

• Palmare: Tenere premuto il tasto c e premere · più volte.
• Windows®: Tenere premuto il tasto F12 e premere Invio più volte.
• Macintosh®: Tenere premuto il tasto F5 e premere Invio più volte.
• iPad®: L'app mostra un prompt. È possibile continuare ad attendere o annullare.

Nota: vedere anche RequestStr, here.

Definire un programma:

Define polynomial()=Prgm
    Request "Enter a polynomial in x:",p(x)
    Disp "Real roots are:",polyRoots(p(x),x)
EndPrgm

 

Eseguire il programma e digitare una risposta:

polynomial()

Risultato dopo avere inserito x^3+3x+1 e selezionato OK:

Le radici reali sono: {-0.322185}

RequestStr

Catalogo >

RequestStr stringaPrompt, var[, DispFlag]

Istruzione di programmazione: Opera in modo identico alla prima sintassi del comando Request, eccetto che la risposta dell’utente viene sempre interpretata come stringa. A differenza di questo, il comando Request interpreta la risposta come espressione a meno che l’utente non la racchiuda tra virgolette (““).

Nota: è possibile utilizzare il comando RequestStr all’interno di un programma definito dall’utente, ma non di una funzione.

Per arrestare un programma che contiene un comando RequestStr in un loop infinito:

• Palmare: Tenere premuto il tasto c e premere · più volte.
• Windows®: Tenere premuto il tasto F12 e premere Invio più volte.
• Macintosh®: Tenere premuto il tasto F5 e premere Invio più volte.
• iPad®: L'app mostra un prompt. È possibile continuare ad attendere o annullare.

Nota: vedere anche Request, here.

Definire un programma:

Define requestStr_demo()=Prgm
    RequestStr “Your name:”,name,0
    Disp “Response has “,dim(name),” characters.”
EndPrgm

 

Eseguire il programma e digitare una risposta:

requestStr_demo()

 

Risultato dopo aver selezionato OK (si noti che l’argomento FlagDispl 0 omette la richiesta e la risposta dalla cronologia):

 

requestStr_demo()

La risposta ha 5 caratteri.

Return

Catalogo >

Return [Espr]

Restituisce Espr quale risultato della funzione. Questo comando viene utilizzato all’interno di un blocco Func...EndFunc.

Nota: utilizzare Return senza alcun argomento all’interno di un blocco Prgm...EndPrgm per uscire da un programma.

Nota per l'inserimento dell'esempio: per istruzioni sull'inserimento di definizioni di programmi e funzioni costituite da più righe, consultare la sezione Calcolatrice del manuale del prodotto.

right() (Destra)

Catalogo >

right(Lista1[, Num]) ⇒ lista

Restituisce i Num elementi più a destra contenuti in Lista1.

Se si omette Num, restituisce l’intera Lista1.

right(stringaOrigine[, Num]) ⇒ stringa

Restituisce i caratteri Num più a destra contenuti nella stringa di caratteri stringaOrigine.

Se si omette Num, restituisce l’intera stringaOrigine.

right(Confronto) ⇒ espressione

Restituisce il secondo membro di un’equazione o di una disequazione.

rk23 ()

Catalogo >

rk23(Espr, Var, varDipendente, {Var0, VarMax}, varDipendente0, incrVar [, tollErrore]) ⇒ matrice

rk23(SistemaDiEspr, Var, ListaDiVarDipendenti, {Var0, VarMax}, ListaDiVarDipendenti0, incrVar[, tollErrore]) ⇒ matrice

rk23(ListaDiEspr, Var, ListaDiVarDipendenti, {Var0, VarMax}, ListaDiVarDipendenti0, incrVar[, tollErrore]) ⇒ matrice

Utilizza il metodo di Runge-Kutta per risolvere il sistema

con varDipendente(Var0)=varDipendente0 nell’intervallo [Var0,VarMax]. Restituisce una matrice la cui prima riga definisce i valori ottenuti di Var come definito da incrVar. La seconda riga definisce il valore del primo componente della soluzione per i valori di Var corrispondenti, e così via.

Espr è il secondo membro che definisce l’equazione differenziale ordinaria (ODE).

SistemaDiEspr è un sistema di secondi membri che definiscono il sistema di ODE (corrisponde all’ordine di variabili dipendenti in ListaDivarDipendenti).

ListaDiEspr è una lista di secondi membri che definisce il sistema di ODE (corrisponde all’ordine di variabili dipendenti in ListaDiVarDipendenti).

Var è la variabile indipendente.

ListaDiVarDipendenti è una lista di variabili dipendenti.

{Var0, VarMax} è una lista a due elementi che indica alla funzione di integrare da Var0 a VarMax.

ListaDiVarDipendenti0 è una lista di valori iniziali di variabili dipendenti.

Se incrVar dà come risultato un numero diverso da zero: sign(incrVar) = sign(VarMax-Var0) e sono restituite soluzioni a Var0+i*incrVar per tutti i valori di i=0,1,2,… tali che Var0+i*incrVar sia in [var0,VarMax] (potrebbe non esserci un valore di soluzione a VarMax).

Se incrVar dà come risultato zero, le soluzioni sono restituite ai valori Var di "Runge-Kutta".

tollErrore è la tolleranza d’errore (predefinita a 0.001).

Equazione differenziale:

y’=0.001*y*(100-y) e y(0)=10

Per vedere l'intero risultato, premere 5, quindi utilizzare 7 e 8 per spostare il cursore.

Stessa equazione con tollErrore impostata su 1.E−6

Sistema di equazioni

con y1(0)=2 e y2(0)=5

root() (Radice)

Catalogo >

root(Valore) ⇒ radice
root(Valore1, Valore2) ⇒ radice

root(Valore) restituisce la radice quadrata di Valore.

root(Valore1, Valore2) restituisce la radice Valore2 di Valore1. Valore1 può essere una costante reale o complessa a virgola mobile, una costante razionale intera o complessa.

Nota: Vedere anche Modello di radice ennesima a pagina, qui.

rotate() (Ruota)

Catalogo >

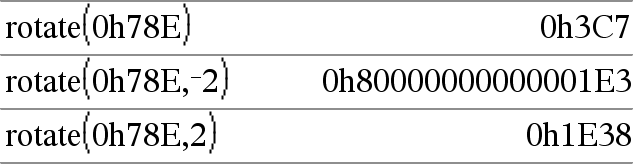
rotate(Intero1[,numRotazioni]) ⇒ intero

Ruota i bit di un numero intero binario. È possibile inserire Intero1 in qualsiasi base numerica; esso viene convertito automaticamente in forma binaria a 64 bit con segno. Se Intero1 è troppo grande per questa forma, un’operazione a modulo simmetrico lo porta all’interno dell’intervallo. Per ulteriori informazioni, vedere ►Base2,  qui.

In modalità base Bin:

 

Per vedere l'intero risultato, premere 5, quindi utilizzare 7 e 8 per spostare il cursore.

Se numRotazioni è positivo, la rotazione avviene verso sinistra. Se numRotazioni è negativo, la rotazione avviene verso destra. L’impostazione predefinita è −1 (ruota a destra di un bit).

Ad esempio, in una rotazione a destra:

In modalità base Esadecimale:

Ogni bit ruota verso destra.

0b00000000000001111010110000110101

L’ultimo bit a destra diventa il primo a sinistra.

dà:

0b10000000000000111101011000011010

I risultati vengono visualizzati nella modalità Base che è stata impostata.

Importante: per inserire un numero binario o esadecimale, utilizzare sempre il prefisso 0b o 0h (è uno zero, non la lettera O).

rotate(Lista1[,numRotazioni]) ⇒ lista

Restituisce una copia di Lista1 ruotata a destra o a sinistra di numRotazioni elementi. Non modifica Lista1.

Se numRotazioni è positivo, la rotazione avviene verso sinistra. Se numRotazioni è negativo, la rotazione avviene verso destra. L’impostazione predefinita è −1 (ruota a destra di un bit).

In modalità base Dec:

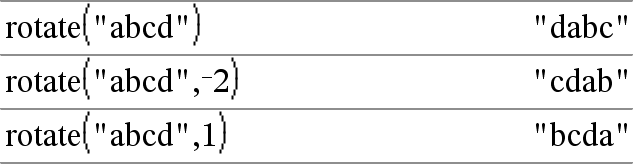
rotate(Stringa1[,numRotazioni]) ⇒ stringa

Restituisce una copia di Stringa1 ruotata a destra o a sinistra di numRotazioni caratteri. Non modifica Stringa1.

Se numRotazioni è positivo, la rotazione avviene verso sinistra. Se numRotazioni è negativo, la rotazione avviene verso destra. L’impostazione predefinita è −1 (ruota a destra di un carattere).

round() (Arrotondamento)

Catalogo >

round(Valore1[, cifre]) ⇒ valore

Restituisce l’argomento arrotondato ad un numero specifico di cifre dopo la virgola decimale.

cifre deve essere un numero intero compreso tra 0 e 12. Se cifre non è incluso, restituisce l’argomento arrotondato alle prime 12 cifre significative.

Nota: la visualizzazione dipende dalla modalità selezionata.

round(Lista1[, cifre]) ⇒ lista

Restituisce una lista degli elementi arrotondati al numero specifico di cifre.

round(Matrice1[, cifre]) ⇒ matrice

Restituisce una matrice degli elementi arrotondati al numero specifico di cifre.

rowAdd() (Somma di righe di matrice)

Catalogo >

rowAdd(Matrice1, rIndice1, rIndice2) ⇒ matrice

Restituisce una copia di Matrice1 nella quale la riga rIndice2 è sostituita dalla somma delle righe rIndice1 e rIndice2.

rowDim() (Dimensione righe matrice)

Catalogo >

rowDim(Matrice) ⇒ espressione

Restituisce il numero di righe di Matrice.

Nota: vedere anche colDim(), qui.

rowNorm() (Norma righe matrice)

Catalogo >

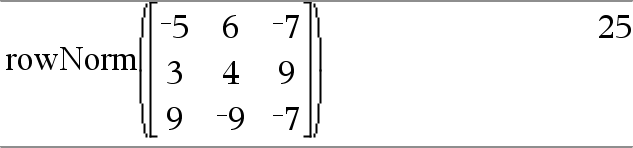
rowNorm(Matrice) ⇒ espressione

Restituisce il massimo delle somme dei valori assoluti degli elementi nelle righe di Matrice.

Nota: tutti gli elementi della matrice devono potere essere semplificati in numeri. Vedere anche colNorm(), qui.

rowSwap() (Inverti righe matrice)

Catalogo >

rowSwap(Matrice1, rIndice1, rIndice2) ⇒ matrice

Restituisce Matrice1 con le righe rIndice1 e rIndice2 scambiate.

rref() (Forma a scalini ridotta per righe)

Catalogo >

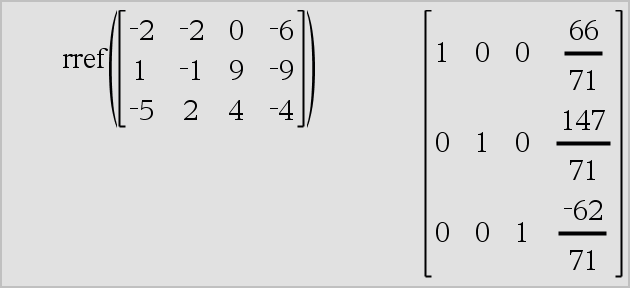
rref(Matrice1[, Tol]) ⇒ matrice

Restituisce la forma a scalini ridotta per righe di Matrice1.

In alternativa, un elemento qualsiasi della matrice viene considerato zero se il suo valore assoluto è minore di Tol. Tale tolleranza viene utilizzata solo se la matrice contiene elementi a virgola mobile e non contiene variabili simboliche alle quali non sia stato assegnato un valore. In caso contrario, Tol viene ignorato.

• Se si usa /· oppure se si imposta la modalità Auto o Approssimato su Approssimato, i calcoli saranno eseguiti in virgola mobile.
• Se Tol viene omesso o non è utilizzato, la tolleranza predefinita viene calcolata come:
5E−14 •max(dim(Matrice1)) •rowNorm(Matrice1)

Nota: vedere anche ref(), here.