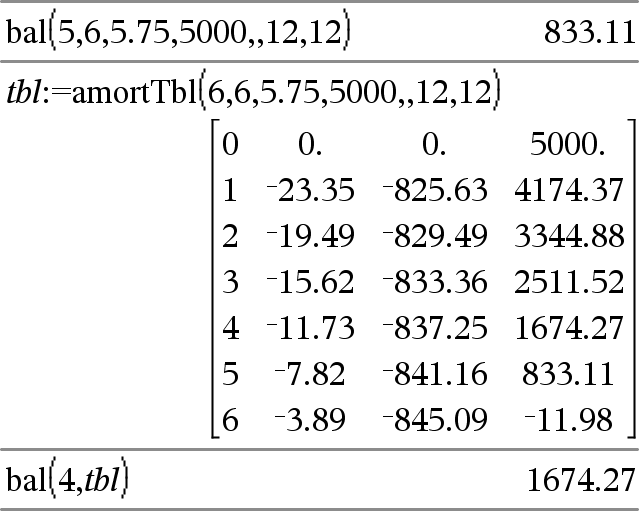
bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [valoreArrotondato])Þvalore

bal(NPmt,tabellaAmmortamento)Þvalore

Funzione di ammortamento che calcola il saldo del piano di rientro dopo una rata specificata.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt sono descritti nella tabella degli argomenti TVM, qui.

NPmt specifica il numero della rata a partire dalla quale deve essere calcolato il saldo.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt sono descritti nella tabella degli argomenti TVM, qui.

valoreArrotondato specifica il numero di cifre decimali di arrotondamento. Impostazione predefinita=2.

bal(NPmt,tabellaAmmortamento) calcola il saldo dopo la rata numero NPmt sulla base della tabella di ammortamento tabellaAmmortamento. L’argomento tabellaAmmortamento deve essere una matrice avente la forma descritta in amortTbl(), qui.

Nota: vedere anche GInt() e GPrn(), qui.

Un numero binario può contenere fino a 64 cifre. Un numero esadecimale può contenere fino ad 16 cifre.

Senza prefisso, Intero1 viene considerato decimale (base 10). Il risultato viene visualizzato in modalità binaria, indipendentemente dalla modalità Base impostata.

I numeri negativi sono visualizzati nella forma “a complemento di due”. Ad esempio,

N1 è visualizzato come

0hFFFFFFFFFFFFFFFF  in modalità base Esadecimale 0b111...111 (la cifra  1 ripetuta 64 volte)  in modalità base Binaria

N263 è visualizzato come 0h8000000000000000  in modalità base Esadecimale e 0b100...000 (63 zeri)  in modalità base Binaria

Se viene indicato un intero decimale esterno alla gamma di una forma binaria con segno a 64 bit, verrà utilizzata un'operazione a modulo simmetrico per portare il valore nell'intervallo appropriato. Considerare i seguenti esempi di valori esterni alla gamma.

263 diventa N263 ed è visualizzato come 0h8000000000000000  in modalità base Esadecimale e 0b100...000 (63 zeri)  in modalità base Binaria

264 diventa 0 ed è visualizzato come 0h0  in modalità base Esadecimale e 0b0  in modalità base Binaria

N263 N 1 diventa 263 N 1 ed è visualizzato come 0h7FFFFFFFFFFFFFFF  in modalità base Esadecimale e 0b111...111 (64  1)  in modalità base Binaria

Intero1 4Base10Þintero

Nota: è possibile inserire questo operatore dalla tastiera del computer digitando @>Base10.

Converte Intero1 in numero decimale (base 10). Le voci binarie o esadecimali devono sempre avere, rispettivamente, il prefisso 0b o 0h.

0b numeroBinario

0h numeroEsadecimale

Zero, non la lettera O, seguito da b o h.

Un numero binario può contenere fino a 64 cifre. Un numero esadecimale può contenere fino ad 8 cifre.

Senza prefisso, Intero1 viene considerato decimale (base10). Il risultato viene visualizzato in modalità decimale, indipendentemente dalla modalità Base impostata.

Intero1 4Base16Þintero

Nota: è possibile inserire questo operatore dalla tastiera del computer digitando @>Base16.

Converte Intero1 in un numero esadecimale. I numeri binari o esadecimali hanno sempre, rispettivamente, il prefisso 0b o 0h.

0b numeroBinario

0h numeroEsadecimale

Zero, non la lettera O, seguito da b o h.

Un numero binario può contenere fino a 64 cifre. Un numero esadecimale può contenere fino ad 16 cifre.

Senza prefisso, Intero1 viene considerato decimale (base 10). Il risultato viene visualizzato in modalità esadecimale, indipendentemente dalla modalità Base impostata.

Se viene indicato un intero decimale troppo grande per una forma binaria con segno a 64 bit, verrà utilizzata un'operazione a modulo simmetrico per portare il valore nell'intervallo appropriato. Per ulteriori informazioni, vedere 4Base2, qui.

binomCdf(n,p)Þlista

binomCdf(n,p,valoreInferiore, valoreSuperiore) Þ numero se valoreInferiore e valoreSuperiore sono numeri, lista se valoreInferiore e valoreSuperiore sono liste

binomCdf(n,p,valoreSuperiore)per P(0{X{valoreSuperiore)Þnumero se valoreSuperiore è un numero, lista se valoreSuperiore è una lista

Calcola la probabilità cumulativa per la distribuzione binomiale discreta con il numero di prove n e le probabilità di successo p per ciascuna prova.

Per P(X { valoreSuperiore), impostare valoreInferiore=0

binomPdf(n,p)Þlista

binomPdf(n,p,ValX)Þnumero se ValX è un numero, lista se ValX è una lista

Calcola una probabilità in corrispondenza di valX per la distribuzione binomiale discreta con il numero n di prove e la probabilità p di successo per ogni prova.