In this lesson you will define a function that will be used to find average velocities of a falling object. You will use this function to calculate and compare average velocities over several different time intervals and then illustrate these velocities.
Dropping a Book
A book was dropped from a height of 0.865 meters. Its height above ground was monitored with a Texas Instruments Calculator-Based Laboratory™ (CBL™). The following table contains data of the book's height in meters versus time in seconds.
| Time | 0.00 | 0.02 | 0.04 | 0.06 | 0.08 | 0.10 | 0.12 |
| Height | 0.865 | 0.858 | 0.848 | 0.836 | 0.819 | 0.799 | 0.775 |
| Time | 0.14 | 0.16 | 0.18 | 0.20 | 0.22 | 0.24 | 0.26 | 0.28 |
| Height | 0.748 | 0.716 | 0.681 | 0.642 | 0.600 | 0.554 | 0.506 | 0.454 |
- Enter the data in the Statistics/List Editor
- Make a scatter plot of height (y) versus time (x)
Click here to review the Keystrokes to enter the data.
Click here to review the Keystrokes to create a scatter plot.
The Window shown is [-0.028, 0.308] x [0.4129, 0.9061] with xscl = 0.014 and yscl = 0.02055.
Calculating Average Velocity
Average velocity is defined to be the change in position divided by elapsed time.
If h1 is the height at time t1 and h2 is the height at time t2,
h2 – h1 represents change in position,
t2 – t1 represents elapsed time, and
represents average velocity.
Defining a Function of Several Variables
The TI-89 calculator can define a function that will compute average velocity using the four values t1, h1, t2 and h2.
- Define avel(t1,h1,t2,h2)=(h2–h1)/(t2–t1)
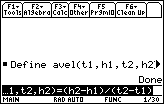
The function avel will return the average velocity between the two points (t1, h1) and (t2, h2).
Finding the Average Velocity over t = 0 to t = 0.28
Use the function avel to find the average velocity from (0, 0.865) to (0.28, 0.454).
- Enter the command avel(0, 0.865, 0.28, 0.454)
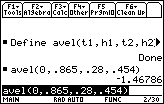
The average velocity over the interval from t = 0 to t = 0.28 was approximately –1.468 m/sec.
The negative sign means the object is moving downward.
Finding the Average Velocity over Subintervals
7.1.1 Find the average velocity for
- the subinterval from t = 0 to t = 0.16 by using the points (0, 0.865) and (0.16, 0.716), and
- the subinterval from t = 0.16 to t = 0.28 by using the points (0.16, 0.716) and (0.28, 0.454).
Click here for the answer.
7.1.2 The second average velocity has a larger magnitude than the first. What does this tell you about the falling object? Click here for the answer.
Average Velocity as Slope
The average velocity from (0, 0.865) to (0.28, 0.454) is also the slope of the line through the corresponding points on the scatter plot. You can graph this line with the DrawSlp (Draw Slope) command, which is found in the catalog. It requires the coordinates of a point (x, y) and a slope m, and its syntax is
Because average velocity is also the slope, you can use the previous result as the desired slope.
-
Store the slope in the variable m with the command avel(0, 0.865, 0.28, 0.454)
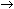m
 |
|||
|
|||
|
|||
-
Paste DrawSlp to the Edit Line by pressing
to jump to the 'd' section in the catalog, scrolling down to DrawSlp, and pressing
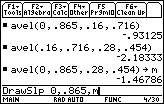
- Finish the command DrawSlp 0,0.865,m
Notice there are no parentheses in this command.
-
Execute the command by pressing
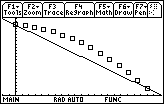
The slope of this line is the average velocity for the entire interval given in the table.
Illustrating Slopes of Subintervals
The average velocity of the book during the subinterval from t = 0 to t = 0.16 can be illustrated by drawing the line that contains the points (0, 0.865) and (0.16, 0.716).
-
Compute and store the slope of the line with the command
avel(0, 0.865, 0.16, 0.716)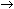
m
- Auto-paste the command "DrawSlp 0, 0.865,m" from the History Area to the Edit Line
-
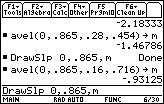
Execute the DrawSlp command by pressing
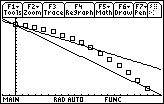
Finally, draw the line associated with the average velocity from (0.16, 0.716) to (0.28, 0.454).
-
avel(0.16, 0.716, 0.28, 0.454)
m
- DrawSlp 0.16, 0.716, m
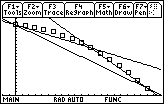
The slope of each line is equal to an average velocity over an interval.
Press
to regraph the scatter plot without the lines in preparation for lesson 7.2.