The average velocities computed in Lesson 7.2 were examples of right-hand

Expressions of the form and are called difference quotients because each is the quotient of two differences.

difference quotients. The term "right-hand" refers to the fact that each average velocity was evaluated over an interval in which (0.16, 0.716) remained fixed and the other points had x-values that were larger than 0.16 and approached 0.16 from the right. In this lesson you will explore left-hand and symmetric difference quotients.

Finding Left-hand Difference Quotients

A left-hand difference quotient of a function is found by approaching the fixed point from the left.

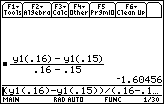
Determine the left-hand difference quotient of the function stored in y1 by using the points
(0.16, y1(0.16)) and (0.15, y1(0.15)).

• Evaluate the command (y1(0.16)–y1(0.15)) / (0.16–0.15)

Instantaneous Velocity Using Left-hand Difference Quotients

In Lesson 2 the instantaneous velocity at t = 0.16 was found to be –1.6496 using right-hand difference quotients. Would successive left-hand difference quotients produce the same result?

7.3.1 Evaluate left-hand difference quotients over the following intervals:

t = 0.159 to t = 0.16 (elapsed time = 0.001 seconds)

t = 0.1599 to t = 0.16 (elapsed time = 0.0001 seconds)

t = 0.15999 to t = 0.16 (elapsed time = 0.00001 seconds)

Click here for the answer.

Find the limit of the left-hand difference quotient as the elapsed time approaches 0.

• Evaluate limit( (y1(0.16) – y1(0.16–h)) / h, h, 0)

The limit of the left-hand difference quotients produces the same instantaneous velocity as the limit of right-hand difference quotients. It can be shown in general that for a function f with a in the domain of f, the instantaneous velocity at the point (a, f(a)) can be found by evaluating either of the following limits.

Symmetric Difference Quotients

A symmetric difference quotient is obtained by choosing points evenly spaced on either side of t = 0.16. Will this produce the same result as the left- and right-hand difference quotients?

Evaluate the symmetric difference quotient using the points (0.15, y1(0.15)) and (0.17, y1(0.17)).

• Enter (y1(0.17)–y1(0.15)) / (0.17–0.15)

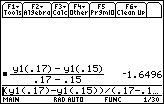
This result is the same as the instantaneous velocity found earlier.

7.3.2 Find the symmetric difference quotient for the interval from t = 0.159 to t = 0.161. Is the average velocity for this interval also equal to the instantaneous velocity? Click here for the answer.

Finding the Limit of the General Symmetric Difference Quotient

Values that are equally spaced on either side of t = 0.16 can be written as 0.16 – h and 0.16 + h, where h is some small positive number. The corresponding points are (0.16 – h, y1(0.16 – h)) and (0.16 + h, y1(0.16 + h)), and the general symmetric difference quotient is

Find the limit of the general symmetric difference quotient.

• Enter limit((y1(0.16+h) – y1(0.16–h)) / (2h), h, 0)

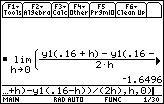
For the quadratic function in this lesson, every symmetric difference quotient gives the instantaneous velocity. Clearly then, the limit of the symmetric difference quotients is also the instantaneous velocity. As stated in the following theorem, this property is true for all quadratic functions.

Theorem

If the function is quadratic, a symmetric difference quotient at a point is equal to the instantaneous velocity at that point.

The TI-89 can be used to prove the theorem.

Proof

• Start fresh by choosing New Problem from the F6:Clean Up menu
• Define f(x) = ax² + bx + c
  Don't forget to include multiplication symbols between a and x² and between b and x.
• Evaluate the symmetric difference quotient

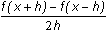
Because the symmetric difference quotient is independent of h,

It can be shown that is an alternate form which can be used to find instantaneous velocity for any smooth function, so a symmetric difference quotient is equal to the instantaneous velocity for any quadratic function.