In this lesson you will investigate a rational function that has both vertical and horizontal asymptotes. You will first display the asymptotes graphically and then you will use tables and the limit command to describe the behavior of the function near these asymptotes.

Asymptote Definitions

A function has a vertical asymptote at x = a if as the input values approach a from at least one side, the magnitude of the output gets large without bound. That is, x = a is a vertical asymptote if and / or .

A horizontal asymptote is a horizontal line that the graph of a function approaches as the magnitude of the input gets large without bound. That is, y = k is a horizontal asymptote of f(x) if and / or . A horizontal asymptote describes the end behavior of a function but a function may cross a horizontal asymptote for small values of the input.

For a rational function, the function is undefined at a vertical asymptote, and the limits as or as will be the same if the function has a horizontal asymptote.

5.1.1 Graph the function in a [-20, 20] x [-10, 10] window. Use the graph to determine as best as you can the vertical and horizontal asymptotes, and write their equations. Click here for the answer.

Vertical Asymptotes When a function has a vertical asymptote, a graphing calculator will often show what appears to be the graph of the asymptote along with the graph of the function. However, the calculator is actually connecting the bottom branch of the graph with the top branch. These two branches should not be connected so the calculator graph is flawed. The graph of a vertical asymptote is not part of the graph of the function.

Finding Vertical Asymptotes

Make a table of values to describe the behavior of the function near the vertical asymptote x = 3.

• Display the Table Setup menu by pressing [TblSet]
• Enter 2.98 for tblStart and 0.01 for 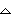tbl and save these values
• Display the table by pressing [TABLE]

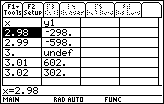
5.1.2 What does the table tell you about the behavior of the function near the vertical asymptote? Click here for the answer.

5.1.3 Use the limit command to confirm that x = 3 is a vertical asymptote by evaluating and . Click here for the answer.

Finding Horizontal Asymptotes

Make a table of values to show the behavior of the function as it approaches the horizontal asymptote y = 2 when x is large and postive.

• Set tblstart = 10 and 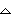tbl = 20 and display the table

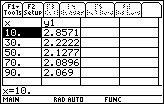
Display the function values when x is large and negative.

• Set tblstart = –10 and tbl = –20 and display the table

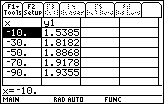
5.1.4 What do the two tables tell you about the behavior of the function as gets large? Click here for the answer.

Using the Limit Function

Verify that y = 2 is a horizontal asymptote by evaluating the limit of the function as x approaches and as x approaches – .

Enter

• limit((2x^2+4x)/(x^2–x–6),x, )

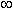  ( is a green feature above the key)

• limit((2x^2+4x)/(x^2–x–6),x,– )

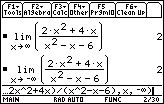
The line y = 2 is the horizontal asymptote of .