In Lesson 1.2 you defined the function f(x) = 2x² – 5x – 3 and found its roots symbolically. In this lesson you will display this function graphically and use the graph to find its roots.

Recalling a Defined Function

Even if you turned off your calculator after completing Lesson 1.2, the function f(x) should still be defined. Verify this by clearing the Home screen and the Edit Line and then entering f(x) on the Edit Line. Click here to see the keystroke sequence to do this.

Graphing a Defined Function

To graph a function you need to place it in the Y= Editor. The Y= feature is found above the key.

You will now define y1= f(x) , set the viewing window, and graph the function

• Display the Y= Editor by pressing [Y=]

Deleting Functions in the Y= Editor You can clear lines in the Y= Editor by moving the cursor to the desired line with the cursor movement keys and then pressing .

Entering a Defined Function into the Y= Editor

Make sure y1 is clear and the cursor is by y1.

• Enter f(x) by pressing [F]

As you press the keys, the expression is displayed in the Edit Line. When you press , the function appears by y1.

Setting the Viewing Window

Before you graph the function, you need to specify the

The viewing window represents the portion of the coordinate plane displayed on the Graph screen. By setting Window variables, you can define the viewing window's boundaries and other attributes. Each of the graphing modes (function, parametric, etc.) has it's own independent set of window variables.

viewing window .

• Display the viewing window screen by pressing

The values of the parameters of the Viewing Window determine the size of the window in which the graph appears.

• xmin and xmax determine the coordinates of the left and right sides of the window
• ymin and ymax determine the bottom and top of the window
• xscl and yscl determine the spacing between the hash marks on the x-axis and the y-axis
• xres determines the spacing between the pixels that are plotted on the graph

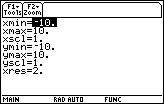
The window values shown above are appropriate for our function's graph, so we will keep them. If you need to change your window values to match those shown above, you can do this by moving the cursor to the appropriate line with the cursor movement keys and then entering the desired values.

Displaying a Graph

Display the graph when the window values are correct.

• Display the graph by pressing [GRAPH].
  The [GRAPH] feature is above the key on the Home screen.

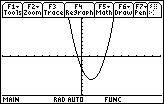
Finding Roots Graphically

You can find the roots of the function from the graph screen.

• Display the MATH menu by pressing
• Select the Zero feature by pressing

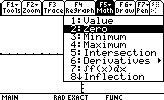
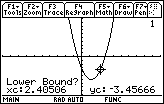
You will see the graph and a prompt for a lower bound, as shown at right below.

Graph Math menu	Specify the lower bound

• Use the cursor movement keys to move the cursor until it is just to the left of the larger root and press , or simply type a number to the left of the zero, say 2.

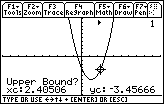
After you press , a small marker appears at the top of the graph above the lower bound, as shown at the top of the graph at right below. The calculator then asks you to indicate an upper bound.

Move the cursor	Then press Enter

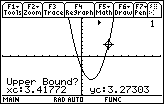
• Use the cursor movement keys to move the cursor until it is just to the right of the root and press , or simply type a number to the right of the zero, say 4.

Move the cursor	Press Enter

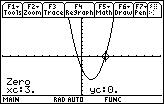
The root is x = 3.

1.3.1 Use the Math Zero feature to find the other root. Click here for the answer.