In this lesson you will define and investigate a function symbolically on the Home screen.

The function you will define is f(x) = 2x² – 5x – 3. If you make mistakes in the following keystroke commands, you can backspace and erase by pressing .

Defining a Function

From the Home screen,

• Select the Other menu by pressing
• Paste the Define command to the Edit Line by pressing or
• Paste the letter "f" to the Edit Line by pressing

Notice is a purple key.

1.2.1 What is printed in purple above the key? Click here for the answer.

• Now press .

The Variable x vs. the Symbol for Multiplication, x The key in the left column of keys is used to enter the variable "x". The key in the right column is used for multiplication.

• Finish entering the command "Define f(x) = 2x² – 5x – 3" by pressing . Your screen should look like the one below.

Negation vs. Subtraction Be careful not to confuse the black subtract key with the gray negate key . The negate key multiplies the following argument by negative one, which may not give the same result as subtraction. For example, pressing gives a result of 2 because 5 minus 3 is 2. However, pressing gives a result of -15 because the calculator multiplies 5 by -3.

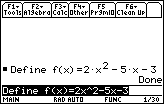
Evaluating a Function

Now that you have successfully defined the function f(x) = 2x² – 5x – 3, you can evaluate the function at x = 2.

• Enter f(2) by pressing .

Keystroke Instruction for Modified Keys From now on when instructed to enter a purple , yellow or green feature, the keystroke instructions will show the , or key followed by the corresponding symbol that is shown above the key rather than the key itself. The symbol will be contained in brackets rather than enclosed in a box. For example, the keystroke instructions to enter "f" into the Edit Line will say [F] rather than .

Editing the Last Expression in the Edit Line

If you want to evaluate the function at x = 3 just after evaluating f(2), you can edit the current expression in the Edit Line rather than typing in the entire expression "f(3)."

• Place the cursor at the end of the current expression on the Edit Line by pressing
• Move to the expression just inside the parenthesis by pressing
• Backspace and erase the 2 by Pressing
• Insert 3 by pressing
• Display the result by pressing

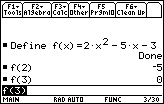
Finding Roots (or Zeros) of Functions

As shown above, one of the

A root, or zero, of a function is a value of the independent variable that makes the function zero, i.e., solutions to f(x) = 0 are the roots, or zeros of the function f.

roots of the function f(x) = 2x² – 5x – 3 is x = 3.

1.2.2 Evaluate the function at other values of x until you find the other root. When you have found the other root, click here for the answer.

If you tried many values until you found the second root, you used a method called

Guess and check is a method for finding roots (or zeros) of a function. First guess a value for the variable and find the value of the function. If the value of the function is not zero, pick another value of the variable and find the value of the function. Continue in this manner until a root is found.

guess and check .

The Algebra Menu's Solve Command

The Algebra menu ( on the Home screen) contains the solve( command, which can help you find the roots directly. To find the roots of f(x) = 2x² – 5x – 3 by using solve(, follow the steps below.

• Go to the Home screen by pressing
• Clear the History Area by pressing
• Clear the Edit Line by pressing
• Select solve( by pressing or
• Complete the command "solve( f(x) = 0, x)" by pressing [F]

The roots are x = 3 and .

The Algebra Menu's Factor Command

You may see the relationship between the roots and the factors of f(x) by using the factor( command.

• Paste the factor( command to the Edit Line by pressing
• Complete the command "factor(f(x), x)" by pressing [F]

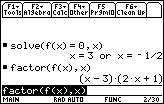
The factors are (x – 3) and (2x + 1). Notice that the roots of the factors, (x – 3) and (2x + 1), are also the roots of the original function, x = 3 and .