1. The Maclaurin series for y = tan^-1(x) is . What is the fifth-order Maclaurin polynomial for y = tan^-1 (x)?
2. Graph y = tan^-1 (x) with a thick graphing style. In the same window graph the 5th-, 9th-, and 13th-order Maclaurin polynomials for this function. Estimate the interval of convergence for the series based on your graph.
3. Find the second-order Taylor polynomial centered at 2 for y = e^x.
4. The second order Maclaurin polynomial for f(x) = e^x is 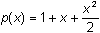. Use this series to find the fourth-order Maclaurin polynomial for y = e^x2 .
5. Graph y = e^x2 with a thick graphing style together with the fourth-order Maclaurin polynomial for y = e^x2.

Click here to check your answers.