1 + x

1 + x + x²

1 + x + x² + x³

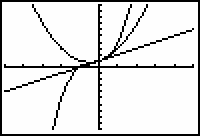
The graphs appear to coincide when x is between -0.5 and 0.5.

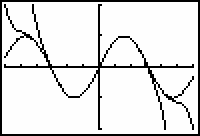
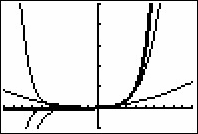
The partial sums appear to converge to y = sin x.

[-10,10,1] x [-50,250,50]

As more terms are added, the interval where each partial sum matches e^x widens.

f(-0.5) 0.60653

p(-0.5) = 0.625

f(0.5) 1.6487

p(0.5) = 1.625

In each case, the values of the function and the approximating polynomials are close.

Letting f(x) = ln(1 + x), the table below lists the coefficients of the fifth-order Maclaurin polynomial.

The fifth-order Maclaurin polynomial approximates f(x) = ln(1 + x) for values of x close to 0.

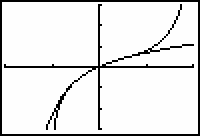
[-2, 2, 1] x [-3, 3, 1]

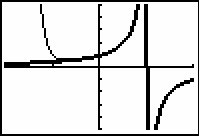
is the second-order Taylor polynomial for ln x centered at 1.

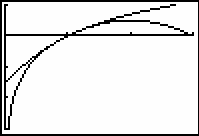
[0, 3, 1] x [-3, 1, 1]

1 - (x - 1) + (x - 1)² is the second-order Taylor polynomial for 1/x centered at 1.

[0, 3, 1] x [-1, 3, 1]

The interval of convergence appears to be (-1,1).

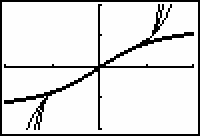
[-2, 2, 1] x [-2, 2, 1]

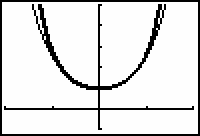
[-2, 2, 1] x [-1, 5, 1]