In Lesson 24.2 you found Maclaurin series that approximate functions near x = 0. This lesson investigates how to find a series that approximates a function near x = a, where a is any real number.

A Taylor Series

Given a function f that has all its higher order derivatives, the series

, where

is called the Taylor series for f centered at a. The Taylor series is a power series that approximates the function f near x = a.

The partial sum is called the nth-order Taylor polynomial for f centered at a.

Every Maclaurin series, including those studied in Lesson 24.2, is a Taylor series centered at zero.

The Taylor Polynomial of e^x Centered at 1

The second-order Taylor polynomial centered at 1 for the function f(x) = e^x can be found by using a procedure similar to the procedure given in Lesson 24.2.

The coefficient of the term (x - 1)^k in the Taylor polynomial is given by . This formula is very similar to the formula for finding the coefficient of x^k in a Maclaurin polynomial where the derivative is evaluated at 0. In this Taylor polynomial, the derivative is evaluated at 1, the center of the series.

The coefficients of the second-order Taylor polynomial centered at 1 for e^x are

f(1) = e

f '(1) = e

So the second-order Taylor polynomial for e^x centered at 1 is , and near x = 1, e^x P₂(x).

The Taylor series for e^x centered at 1 is similar to the Maclaurin series for e^x found in Lesson 24.2. However, the terms in the Taylor series have powers of (x - 1) rather than powers of x and the coefficients contain the values of the derivatives evaluated at x = 1 rather than evaluated at x = 0.

Graphing the function and the polynomial illustrate that the polynomial is a good approximation near x = 1.

• Graph y = e^x and 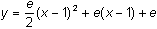in a [-2, 3, 1] x [-3, 10, 1] window.

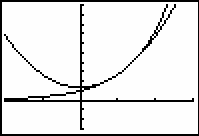
The second-order Maclaurin polynomial you found in Lesson 24.2, , is tangent to f(x) = e^x at x = 0 and has the same concavity as f(x) = e^x at that point. The polynomial , which is centered at x = 1, is tangent to f(x) = e^x at x = 1 and has the same concavity as f(x) = e^x at that point.

24.3.1 Find the second-order Taylor polynomial centered at 1 for the function f(x) = ln x. Graph this polynomial together with f(x) = ln x. Click here for the answer.

Other Taylor Series

The Taylor series for one function can be used to find a Taylor series for a related function.

The third-order Taylor polynomial centered at 1 for f(x) = ln x is .

The derivative of f(x) = ln x is . The derivative of p(x) gives the second-order Taylor polynomial for centered at 1.

24.3.2 Find the second-order Taylor polynomial for centered at 1 using the derivative of p(x) and graph it with . Click here for the answer.

The Taylor Series for cos x²

Other modifications of a Taylor series yield other Taylor-series. For example, replacing each x with x² in the Taylor series for f(x) = cos(x) gives the Taylor series for g(x) = f(x²) = cos(x²).

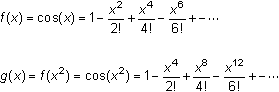
• Graph 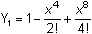and Y₂ = cos(x²) in a [-2,2,1] x [-2,2,1] window.