In this lesson you will study several power series and discover that on the intervals where they converge, they are equal to certain well known functions.

Defining Power Series

A power series is a series in which each term is a constant times a power of x or a power of (x - a) where a is a constant.

Suppose each c_k represents some constant. Then the infinite series

is a power series centered at x = 0 and the infinite series

is a power series centered at x = a.

Finding Partial Sums of a Power Series

Consider the power series

.

Although you cannot enter infinitely many terms of this series in the Y= Editor, you can graph partial sums of the series because each partial sum is a polynomial with a finite number of terms.

Graphing Partial Sums of a Power Series

• Set Graph mode to FUNCTION.

24.1.1 What are the second, third, and fourth partial sums of the power series ?
Click here for the answer.

24.1.2 Graph the second, third, and fourth partial sums of the power series in a [-5, 5, 1] x [-10, 10, 1] window. On what interval do the graphs appear to coincide? Click here for the answer.

Defining an Infinite Geometric Series

Recall that an infinite geometric series can be written as a + ar + ar² + ar³ + ... + ar^k + ..., where a represents the first term and r represents the common ratio of the series. If | r | < 1, the infinite geometric series a + ar + ar² + ar³ + ... + ar^k + ... converges to .

The power series is a geometric series with first term 1 and common ratio x. This means that the power series converges when | x | < 1 and converges to on the interval (-1, 1).

Visualizing Convergence

The graphs of several partial sums can illustrate the interval of convergence for an infinite series.

• Graph the second-, third-, and fourth-degree polynomials that represent partial sums of .
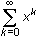• Graph .
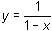• Change the graphing style for 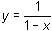to "thick" to distinguish it from the partial sums.

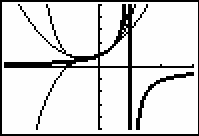
On the interval (-1,1) the partial sums are close to . The interval (-1,1) is called the interval of convergence for this power series because as the number of terms in the partial sums increases, the partial sums converge to on that interval.

24.1.3 Graph the tenth-degree partial sum of and the function y = 1/(1 - x) in a [-2,2,1] [-5,5,1] viewing window. Use thick graphing style for y = 1/(1 - x). Click here for the answer.

Another Power Series

Consider the power series

• Graph the seventh-, eleventh-, and fifteenth-degree polynomial partial sums in a
  [-6,6,1] x [-2,2,1] window.

Using Previously Defined Graphing Variables You do not have to enter every term of each partial sum. Enter the expressions below in the Y= Editor by using Y1 and Y2 from the Y-VARS menu. Y1 = X - X^3/3! + X^5/5! - X^7/7! Y2 = Y1 + X^9/9! X^11/11! Y3 = Y2 + X^13/13! X^15/15! Recall that the factorial symbol can be obtained by pressing .

24.1.4 The partial sums seem to converge to what familiar function?
Click here for the answer.

Adding More Terms to the Partial Sums

As more terms are added to form successive partial sums, more turning points appear and the power series converges to the function y = sin x on the interval (– , ).

Illustrating Convergence of

In Lesson 24.2 you will see that the power series converges to e^x.

Graphs of the second-, fifth-, eighth-, and eleventh-degree partial sums of the power series illustrate that the infinite series converges to y = e^x.

• Set Y₁= e^x and its graphing style to "thick."
• Enter the desired partial sums of 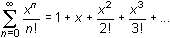into Y₂, Y₃, Y₄ and Y₅, respectively.

  Use the short cut that was described in the Tech Tip for the previous power series to enter the partial sums.

• Try several different windows starting with [-5, 5, 1] x [-5, 5, 1].

24.1.5 What seems to happen to the interval where each partial sum matches the graph of e^x as more terms are added in successive partial sums?
Click here for the answer.