In Lesson 24.1 you explored several power series and their relationships to the functions to which they converge. In this lesson you will start with a function and find the power series that best converges to that function for values of x near zero.
Approximating a Function Near x = 0
Suppose f is some function. A second-degree polynomial p(x) = ax2 + bx + c that satisfies p(0) = f(0),
p'(0) = f'(0), and p"(0) = f"(0), gives a good approximation of f near x = 0. The procedure below illustrates the method by finding a quadratic polynomial that satisfies these conditions for the function f(x) = ex.
Let f(x) = ex and p(x) = ax2 + bx + c.
Use the fact that f and p are equal at x = 0 to find the value of c.
| f(x) = ex | f(0) = e0 = 1 |
| p(x) = ax2 + bx + c | p(0) = a(0)2 + b(0) + c = c |
If c = 1, the function and the polynomial have the same value at x = 0, so p(x) = ax2 + bx + 1.
Using a similar procedure, set the first derivatives equal when x = 0 and solve for b.
| f '(x) = ex | f '(0) = e0 = 1 |
| p '(x) = 2ax + b | p '(0) = 2a(0) + b = b |
If b = 1, the function and the polynomial will have the same slope at x = 0, so p(x) = ax2 + x + 1.
Set the second derivatives equal when x = 0 and solve for a.
| f "(x) = ex | f "(0) = e0 = 1 |
| p "(x) = 2a | p "(0) = 2a |
If a = 1/2, the function and the polynomial will have the same concavity at x = 0.
So
approximates y = ex near x = 0.
Graphs of the Function and the Approximating Quadratic Polynomial
- Graph the functions Y1 = e^X and Y2 = (1/2)X2 + X + 1 in a [-5, 5, 1] x [-2, 10,1] window.
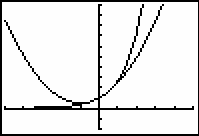
The parabola has the same value, the same slope, and the same concavity as y = ex when x = 0, and the quadratic polynomial is a good approximation for y = ex when x is near 0.
24.2.1 Create a table of values for f(x) = ex and p(x) = (1/2)x2 + x + 1 with TblStart = -1 and
Tbl = 0.1. Compare the values of ex and the quadratic polynomial when x = -0.5 and when x = 0.5.
Click here for the answer.
The General Procedure for Finding Maclaurin Series
The procedure for finding the coefficients of a power series that approximates a function near x = 0 is summarized below, where the function y = f(x) is to be approximated by the power series polynomial
.
- Set the value of p(x) equal to the value of f(x) at x = 0 and solve for c0.
- Set the value of the first derivative p'(0) equal to the value of the first derivative f'(0) and solve for c1.
- Repeat Step 2 and set all of the remaining derivatives of p(x) at x = 0 equal to the corresponding derivatives of f(x) at x = 0 and solve for the remaining coefficients of the power series.
The series found in this fashion is called the Maclaurin series for the function f. Maclaurin series are often useful for integrating functions that do not have elementary antiderivates, for solving differential equations, and for approximating functions by polynomials.
Coefficients in a Maclaurin Series
Letting f(k)(x) denote the kth derivative of f, it can be shown that in a Maclaurin series the coefficient of the term that contains the kth power of x is given by
.
The table below shows the first four coefficients of the Maclaurin series for f(x) = ex.
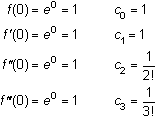
Therefore, the Maclaurin series for ex is
.
The Maclaurin series above is more than an approximation of ex, it is actually equal to ex on the interval of convergence,
.
Every Maclaurin series is centered at x = 0, the interval of convergence is centered at x = 0, and the Maclaurin series values and the function values are very close near x = 0.
The partial sum
is called the nth-order Maclaurin polynomial for f, and if n is relatively large, an nth-order Maclaurin polynomial often approximates the function f well on the interval of convergence.
24.2.2 Find the fifth-order Maclaurin polynomial for y = ln(1 + x) and interpret the result. Click here for the answer.
24.2.3 Graph y = ln(1 + x) and the fifth-order polynomial from 24.2.2. Click here for the answer.