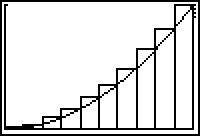
In Lesson 17.1 you used right-hand rectangles to approximate the area of the region bounded by the graph of f(x) = x², the vertical line x = 1, and the x-axis. In this lesson you will use left-hand Riemann sums to approximate the same area.

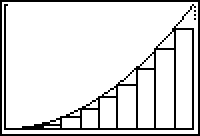
The sum of the areas of the rectangles shown above is called a left-hand Riemann sum because the left-hand corner of each rectangle is on the curve.

Defining the Left-Hand Sum Function

Suppose that the area under the curve y = f(x) and above the x-axis between the lines x = a and x = b is approximated using left-hand rectangles. A function similar to the one defined in Lesson 17.1 can be used to find the sum of the areas of the left-hand rectangles. Modifying the function in Y₂ can create the new function.

• Open the Y= editor and move the cursor to Y₂.

The first left-hand x-coordinate is found by letting k = 0 and the last left-hand x-coordinate is found by letting k = n – 1. This replaces the first right-hand x-coordinate found by letting k = 1 and the last right-hand x-coordinate found by letting k = n.

• Change the initial value and ending value of the sum function from "1, N" to "0, N –1"

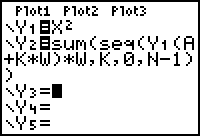
The function Y₁ = X² should still be defined from Lesson 17.1. The following exploration uses the same procedure that was used to find the right-hand Riemann sum with four rectangles, except this time the left-hand Riemann sum function will be used to approximate the area under the curve.

• Return to the Home screen.
• Store 0 in A.
• Store 1 in B.
• Store 4 in N.

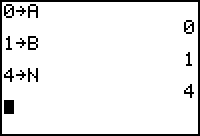
• Store (B - A)/N in W.
• Paste Y₂ to the Home screen and press to evaluate the left-hand Riemann sum.

The left-hand Riemann sum with 4 rectangles is approximately 0.21875 square units.

Evaluate the left-hand Riemann sum for ten rectangles.

• Store 10 in N.
• Redefine W by recalling and executing the command .
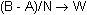• Evaluate the new sum by entering Y₂ on the Home screen again and pressing .

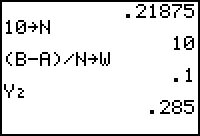
The sum with 10 left-hand rectangles is 0.285 square units.

17.2.1 Evaluate the left-hand Riemann sum using 50 rectangles and using 100 rectangles.

Click here for the answer.

The areas found using left-hand rectangles appear to converge to the same limit as the areas found using right-hand rectangles: 1/3 square unit.

When the number of rectangles approaches infinity, the left-hand Riemann function has the same limit as the right-hand Riemann function. That is, the area under the curve can be found by using either right or left Reimann sum limits as the number of rectangles approaches infinity because they produce the same result. This is true in general for continuous functions. In fact, one can choose any x-value in each subinterval to determine the height of the corresponding rectangle and the limit will still be the same as N goes to .

Many times the midpoint of each subinterval is used to compute the height of each rectangle. Using midpoints usually reduces the error in the approximation of the area under the curve.

The AREA Program

A program created for the TI-83 can be used to illustrate the rectangles that approximate the area under a curve. The program AREA draws the rectangles associated with left, right and

Midpoint Riemann sums are obtained by using the midpoint of each subinterval on the x-axis to determine the height of the corresponding rectangle.

midpoint Riemann sums under a curve and displays the sum of the areas associated with each type. It was used to create the pictures of Riemann sum rectangles earlier in this lesson and in Lesson 17.1. With this program you can create similar visual representations.

Downloading the AREA Program

• Click here to download the program AREA
• Choose to save the file
• Save the file on your local hard disk in a folder that you can access later

Transferring the Program to the TI-83

Click here to get information about how to obtain the needed cable and to review the procedure to transfer the program from your computer to your calculator.

• Transfer the program AREA to your TI-83 calculator
• Clear the Home Screen

Using the AREA Program

The following procedure illustrates the approximate area of the region bounded by the graph of f(x) = x² above the x-axis over the interval [0, 1] by drawing rectangles associated with left, right, and midpoint Riemann sums.

The function X² should be stored in Y₁ in the Y= Editor. Make sure that Y1 is selected.

• Clear the function in Y₂.
• Define the viewing window as [0, 1, 1] x [0, 1, 1].
• Return to the Home screen.
• Press , move the cursor to the line containing AREA and press to paste the command prgmAREA to the Home screen.

 

• Run the program by pressing .

You should see a prompt for the value of A, the left side of the region.

• Enter 0 and press .

Now you should see a prompt for the value of B, the right side of the region.

• Enter 1 and press .

Next you see a prompt for the number of subintervals, i.e., the number of rectangles.

• Enter 10.

The graph of f(x) = x² with the left-hand rectangles will be displayed when you press . The pause indicator (four vertical dots) should appear in the upper right-hand corner of the screen.

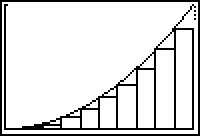
The screen above illustrates using left-hand rectangles to approximate the area under the curve.

Viewing the Subsequent Screens

Subsequent screens of the program display the approximations obtained using left-hand, right-hand, and midpoint Riemann sums, along with illustrations of the rectangles used in the right-hand and midpoint Riemann sums.

• Display the left-hand Riemann sum by pressing .

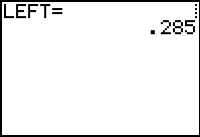
The left-hand Riemann sum using 10 rectangles is 0.285 square units.

• Display the right-hand rectangles by pressing .

• Move through the remaining screens by repeatedly pressing .

You should see the right Riemann sum, the illustration of midpoint rectangles, and finally the midpoint Riemann sum.

The sums of the areas of the ten rectangles used to approximate the area of the region using left, right, and midpoint rectangles are 0.285, 0.385, and 0.3325 square units, respectively.

Run the program again several times to illustrate convergence of the Riemann sums. Try 25 rectangles and 50 rectangles.

17.2.2 What happens when you try 100 rectangles? Click here for the answer.

The AREA program can be used to find the Riemann sums that approximate the area under different curves and over different intervals on the x-axis. Simply change the function defined in Y₁ and enter different values for A, B and N.

Ending a Running Program You can end a program that is running by pressing and then selecting 1:Quit.

17.2.3 Use the AREA program on the region under f(x) = 2x + 1 between x = 0 and x = 3 with 6 rectangles, and find the approximate area using left-hand, right-hand, and midpoint rectangles. Use the window [0, 3, 1] x [0, 8, 1].

Click here for the answer.