Module 17 - Riemann Sums and the Definite Integral

Module 17 - Answers

Lesson 1

Answer 1

17.1.1

Rectangle x-coordinate Height
(y-coordinate) Width Area

1 0.25 0.0625 0.25 0.015625

2 0.50 0.25 0.25 0.0625

3 0.75 0.5625 0.25 0.140625

4 1.00 1 0.25 0.25

Total 0.46875

Answer 2

17.1.2 The approximation of the area under the curve obtained when using 50 rectangles is 0.3434 square units and when using 100 rectangles is 0.33835 square units.

Answer 3

17.1.3 These approximations appear to be converging to about 0.33.

Lesson 2

Answer 1

17.2.1 The approximate areas found by using 50 rectangles and by using 100 rectangles are 0.3234 square units and 0.32835 square units, respectively.

Answer 2

17.2.2 The rectangles are so thin the area below the curve appears to be shaded completely.

Answer 3

17.2.3

The left-hand Riemann sum is 10.5 square units, the right-hand Riemann sum is 13.5 square units, and the midpoint Riemann sum is 12 square units. The left-hand Riemann rectangles are shown above.

Lesson 3

Answer 1

17.3.1

The area bounded by y = 2x + 1 above the x-axis between the vertical lines x = 0 and x = 3 is 12 square units.

Answer 2

17.3.2

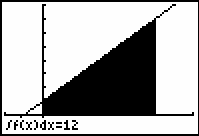
We used the window [-1, 4, 1] x [-1, 8, 1] to draw the figure.

A very good estimate of the area under the curve g(x) = 2x + 1 between x = 0 and x = 3 is 12 square units.

Self Test

Answer 1

The right-hand Riemann sum is 0.3025 square units.

Answer 2

The left-hand Riemann sum is 0.2025 square units.

Answer 3

The midpoint Riemann sum is 0.24875 square units.

Answer 4

The Home screen command used to compute the definite integral is fnInt(X^3,X,0,1).

Answer 5

The area under f(x) = x³ above the x-axis between x = 0 and x = 1 is approximately 0.25 square units, as shown in the screen below.