This lesson investigates finding the definite integral, a basic construct of calculus, using the TI-83.

For a given function over a given x-interval, the limit of the Riemann sum as the number of rectangles approaches infinity is called a definite integral. The notation used to represent a definite integral is . If a < b and f(x) is non-negative on the interval [a, b], the integral represents the exact area under the curve y = f(x) above the x-axis between x = a and x = b. The values of a and b are called the limits of integration.

There are two features on the TI-83 that approximate a definite integral:

1. fnInt, which is found in the Math menu.
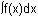2. , which is found in the Graph screen's CALC menu.

Both do the same thing and will always give the same answer.

Using the fnInt Command

The area under the curve f(x) = x² above the x-axis between x = 0 and x = 1 is given by . Use the fnInt command on the Home screen to approximate this integral by following the procedure below.

• Go to the Home screen.
• Clear the Home Screen by pressing
• Paste the Definite Integral command (fnInt) to the Home screen by pressing and selecting 9:fnInt(.

The Definite Integral Command The syntax for finding a definite integral using the fnInt command is fnInt(expression, var, lower, upper)

• Complete the command fnInt(X²,X,0,1).
• Execute the command by pressing .

The exact value is 1/3. The fnInt command gives an approximation, and one cannot always count on it being all that accurate. However, for "typical" functions on reasonably sized intervals, it will be.

17.3.1 Approximate using the fnInt command and interpret the result.

Click here for the answer.

Using the Graphical Definite Integral

Another way to evaluate a definite integral is by graphing the function and using the Definite Integral function, , which is found in the CALC menu of the Graph screen.

• Graph Y₁ = X² in the window [-0.5, 1.5, 1] x [-0.5, 2, 1].

Viewing Window Values When Using When using the feature on the Graph screen, the window interval [xmin, xmax] must contain the interval [a, b] that denotes the interval of integration. The window interval does not have to be the same as the interval of integration.

• Select 7: from the CALC menu.

• When prompted, enter 0 for the lower limit and 1 for the upper limit.

Entering Limit Values Typing the value and pressing is a quick way to set a limit. You may also use the arrow keys to trace to each value and then press but the arrow keys won't generally give you the exact value you want to use.

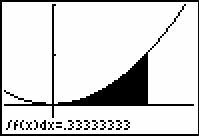
The Definite Integral command of the Graph screen's CALC menu shades the area and gives a decimal approximation of the integral.

17.3.2 Find the area under the curve g(x) = 2x + 1 between x = 0 and x = 3 by using the Definite Integral command in the CALC menu of the Graph screen. Use the window [0, 3, 1] x [-2, 10, 1].

Click here for the answer.