In Lesson 4.1 you graphed a function and its inverse relation parametrically. In this lesson you will use the same method to graph the inverse relation of a sine function. By restricting the values of Tmin and Tmax you will define the inverse relation so it is a function, also.

Inverse Sine

Explore the inverse of the sine function by simultaneously graphing the sine function and its inverse using parametric equations.

• Turn off any active scatter plots.
• Select the Parametric and Simultaneous modes in the MODE menu.

• Clear any equations in the Y= editor and enter the sine function, 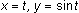, and its inverse function, 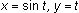, making the sine function thicker.

• Display the graphs in a [-2 , 2 , 0.1] x [-9.5, 9.5, 1] x [-2 , 2 , 1] window.

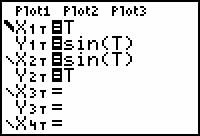
Notice that as the sine function waves about the x-axis, its inverse waves about the y-axis. Because there is more than one y-value associated with some x-values, the inverse relation is not a function.

Restricting the Domain of Sine

The inverse of the sine function is not a function. But if you restrict the domain of the sine function so that each y-value in [-1, 1] occurs only once, then the inverse of this restricted function will also be a function.

• Change the values of Tmin and Tmax to the values shown below.
  
  

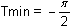
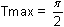
• Display the graphs of both the sine function and it's inverse again but use regular line style for the sine function

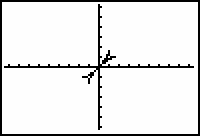
The inverse of this restricted function is a function, however the viewing window is not a good one.

• Enter the following window values:

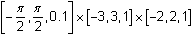
Display only the inverse function by unselecting X_1T and Y_1T , as described below.

• Press then move the cursor onto the "=" sign beside X_1T and press .
  The "=" signs for X_1T and Y_1T should no longer be highlighted. This means X_1T and Y_1T are no longer selected for graphing and will not be displayed.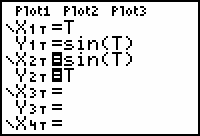
  

• Display the graph of the inverse sine by pressing

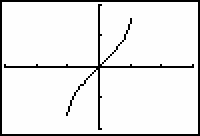
Restricting the domain of y = sin(x) also restricted the range of the inverse relation, which forced each input of the inverse to have exactly one output. The resulting inverse is the function y = sin^-1x , which is also written as y = arcsin x.

Square Window Ratio Window values where the ratio of will produce graphs with equal units on both axes. The ZSquare feature in the ZOOM menu is helpful in finding window values with these proportions.