In the previous lesson you started with an equation and found the corresponding graph by looking at the transformations of the basic graph. A more realistic situation might be to start with a graph of real-world data and then find an equation to fit the data. This can be done on your TI-83 using regression. If the data appear to be sinusoidal, then you can use sine regression. In this lesson you will download data sets produced by a turning fork to your calculator and explore finding the equation that fits the data.

Tuning Fork Data

A vibrating object that disturbs the surrounding air and causes the air molecules to vibrate produces sound. These vibrations cause a periodic change in air pressure that travels through the air much like ripples on a body of water. The air pressure waves are more commonly called sound waves. Although most sounds are a combination of many different sounds, the sound from a turning fork is a single tone that can be described mathematically using a transformed sine function.

A Texas Instruments CBL™ and microphone probe were used to measure a sound wave from a tuning fork. The information in the data will allow you to determine the specific note that was sounded.

Downloading the Data to Your Computer

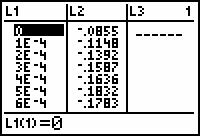
• The data are at the two links L1 and L2. Right-click on each link and choose to save the link as a file on your computer. L1, L2
• Save the files on your local hard disk on the desktop or in a folder that you can access later.

Transferring the Data to the TI-83

Click here to get information about how to obtain the needed cable and to review the procedure to transfer the lists from your computer to your calculator.

• Send the lists L1 and L2 from your computer to your TI-83.
• Display the Stat List editor to confirm that the lists were stored.

Plotting the Data

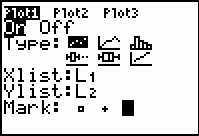
• Define a scatter plot with L1 in the X-list and L2 in the Y-list.
• Select dots as the Mark type.

• Select ZoomStat from the ZOOM menu and display the graph.

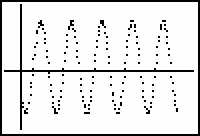
Sine Regression

Because the graph appears to be a transformed sine function, perform sine regression and store the regression equation.

• Open the STAT CALC menu by pressing .
• Highlight C:SinReg by pressing repeatedly or by pressing once.

• Paste the SinReg command to the Home screen by pressing
• Complete the sine regression command "SinReg L1,L2,Y1".
  Recall that L1 and L2 are above and , and that Y1 is found by pressing .

• Execute the command by pressing .

After a minute or two a sine equation that fits the data will be displayed on the Home screen and stored in Y1.

The Forms

Notice that the regression equation is slightly different from the form y = Asin[B(x + C] + D described in Lesson 4.2. A, B and D are the same as the values in the regression equation, but the value of C in the transformed equation is found by dividing the value of C in the regression equation by the value of B. B must be factored out to determine the horizontal shift of the transformed graph.

The transformed regression equation has the characteristics listed below.

A 0.202	Compress vertically by a factor of 0.202.
B 1609	The period of the transformed graph is
	Horizontal shift right 0.00160 units.
D 0.014	Vertical shift up by 0.0141 units.

• Press to see the graph of the regression equation along with the scatter plot.

The graph and scatter plot in the ZoomStat window

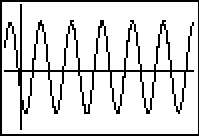
Period and Frequency

The period of this sine wave is , which indicates that it takes approximately 0.004 seconds per cycle. The frequency, which is the reciprocal of the period, is cycles per second.

The Tuning Fork's Note

A frequency of 256 cycles per second is the frequency of the note middle C, so the tuning fork must be a "C".

4.3.1 The period is the distance from one peak to the next peak. If another tuning fork were used with a higher frequency than the tuning fork in this lesson, how would its graph compare with the graph above? Write your response then click here for the answer.