範例:可以由計算分佈來擬合「常態機率密度函數 (Pdf)」分佈模型。
| 1. | 在欄 A 中按一下欄公式儲存格(最上方往下數的第二個儲存格)。 |
| 2. | 按一下 [統計] > [分佈] > [常態機率密度函數 (Pdf)] 來選擇分佈模型。 |
畫面上將會開啟 [常態機率密度函數 (Pdf)] 對話方塊,並顯示可讓您輸入或選取用於計算之引數的欄位。
| 3. | 若有必要,可以按 Tab 以在欄位之間移動並提供每個引數。可以手動輸入值,或從下拉式列表中選取。 |
| - | X 值:按一下下拉式箭號,在問題中選取任何列表以提供用於計算的x值。 |
| - | 平均值:輸入平均值的值,或按一下下拉式箭號選取包含平均值的變數。 |
| - | 標準差:輸入標準差的值,或選取包含標準差的變數。 |
| 4. | 按一下 [繪圖] 核取方塊,檢視在 [數據&統計] 中繪製的分佈。 |
注意:[繪圖] 選項並非在所有的分佈中都可以使用。
| 5. | 按一下 [確定]。 |
[序列&試算表] 將插入兩個欄:一個包含結果名稱,一個包含對應的值。結果將繪製於 [數據&統計] 中。
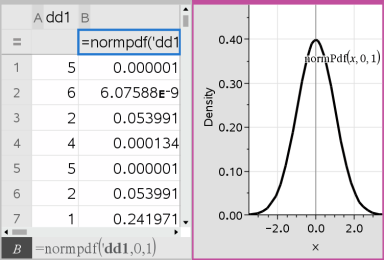
注意:結果連結至原始資料。例如,當變更欄 A 內的值時,方程式將會進行自動更新。
以下是可以在序列&試算表應用程式中使用的分佈。如需關於這些函數的詳細資訊,請參閱《TI-Nspire™ 參考指南》。
| • | 若要返回依據單一值的單一分佈結果,請在單一儲存格中輸入函數。 |
| • | 若要返回依據一組值的一組分佈結果,請在欄公式儲存格中輸入函數。在此情況中,可以指定具有值的列表(欄)。分佈將返回列表內每個值的對應結果。 |
注意:對於支援繪圖選項的分佈函數(normPDF、t 機率密度函數 (Pdf)、χ² Pdf 和 F Pdf)而言,該選項只有在公式儲存格內輸入分佈函數時可以使用。
常態機率密度函數 (Pdf) (normPdf)
計算特定 x 值常態分佈的機率密度函數 (pdf)。預設的平均值為 μ=0,標準差為 σ=1。機率密度函數 (pdf) 為:
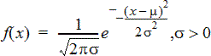
此分佈決定在常態分佈中某個值的出現機率。從公式儲存格調用常態機率密度函數 (PDF) 時,即可使用繪圖選項。
當您從公式儲存格存取分佈時,您必須從下拉式功能表中選取一個有效的列表來避免未知預期的結果。若從儲存格存取,必須指定x-值的數字。分佈會傳回指定值發生的機率。
常態累積分布函數 (Cdf) (normCdf)
在指定平均值的 μ(預設值=0)和標準差 s(預設值=1)的下限和上限之間,計算常態分佈機率。可以按一下 [繪圖(網底區域)] 核取方塊,以共享下限和上限之間的區域。變更為初始下限和上限將會自動更新分佈。
此分佈可幫助於常態分佈中,判斷下限和上限之間任何值出現的機率。這相當於在指定的常態曲線下,尋找下限和上限之間的區域。
反常態 (invNorm)
在平均值 μ 和標準差 s 指定的常態分佈曲線下,計算指定區域的反累積常態分佈函數。
此分佈可在已知百分比的情況下,用於判斷從 0 到 x<1 之區域內的資料 x-值,。
t 機率密度函數 (Pdf)
計算在指定 x 值 t 分佈的機率密度函數 (pdf)。df (自由度)必須 >0。機率密度函數 (pdf) 為:
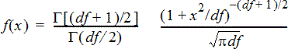
此分佈有助於判斷在母群體標準差為未知且樣本較小時,某個值的出現機率。從公式儲存格調用 t 機率密度函數 (Pdf) 時,即可使用繪圖選項。
t 累積分布函數 (Cdf)
在指定 df(自由度)下限和上限之間,計算「學生-t 」分佈機率。您可以按一下 [繪圖(網底區域)] 核取方塊,以共享下限和上限之間的區域。變更為初始下限和上限將會自動更新分佈。
此分佈有助於用來判斷當母群體標準差為未知時,針對常態分佈的母群體,上下限所定義區間範圍內某個值出現的機率。
反 t (invt)
針對曲線下已知面積的 df(自由度),計算指定的反累積 t-分佈機率函數。
此分佈可用於判斷從 0 到 x<1 的區域中,資料的出現機率。此函數在母群體平均值和/或母群體標準差未知時使用。
c2 Pdf (c2 Pdf())
在指定的 x 值上,計算 c2(卡方)分布的機率密度函數 (pdf)。df(自由度)必須為 >0 的整數。機率密度函數 (pdf) 為:
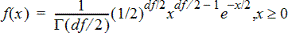
此分布有助於用來判斷來自具有 c2 分布之母群體給定值的出現機率。從公式儲存格調用 c2 Pdf 時,即可使用繪圖選項。
c2 Cdf (c2 Cdf())
針對指定的 df (自由度),計算在下限和上限之間的 c2(卡方)分佈機率。可以按一下 [繪圖(網底區域)] 核取方塊,以共享下限和上限之間的區域。變更為初始的下限和上限將會自動更新分佈。
此分佈有助於用來判斷在具有 c2 分佈之母群體指定範圍內,某個值的出現機率。
F Pdf (F Pdf())
在指定的 x 值上,計算 F 分佈的機率密度函數 (pdf)。分子 df (自由度)和分母 df 必須為 >0 的整數 。機率密度函數 (pdf) 為:
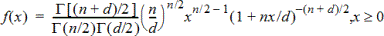
|
其中 |
n = 分子的自由度 |
此分佈有助於判斷兩個樣本擁有相同變異數的機率。從公式儲存格調用 F Pdf 時,即可使用繪圖選項。
F Cdf (F Cdf())
針對指定 dfnumer (自由度)和 dfDenom 的下限和上限之間,計算 F 分佈機率。可以按一下 [繪圖(網底區域)] 核取方塊,以共享下限和上限之間的區域。變更為初始的下限和上限將會自動更新分佈。
此分佈有助於判斷單次觀測落在上下限之間範圍內的機率。
二項式機率密度函數 (Pdf) (binomPdf())
針對具有指定 numtrials 的離散二項分布,計算 x 的機率,以及每次試驗的成功機率 (p)。x 參數可以是整數或整數的序列表。0{p{1 必須為真。numtrials 必須為 >0 的整數。若沒有指定 x,則會傳回一個從 0 到 numtrials 的機率列表。機率密度函數 (pdf) 為:
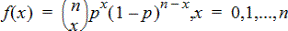
其中n = numtrials
此分佈有助於判斷在試驗 n 上,成功/失敗試驗中的成功機率。例如,您可以使用此分佈,預測在第五次拋錢幣時得到正面的機率。
二項式累積分佈函數 (Cdf) (binomCdf())
計算 n 次試驗和每次試驗成功機率 p 的離散二項分佈累積機率。
此分佈有助於用來判斷在完成所有試驗前,某次試驗的成功機率。例如,如果投幣時得到正面表示成功,而您計畫投擲硬幣 10 次,此分佈會預測在 10 次投幣中至少會得到一次正面的機會。
反二項式 (invBinom())
给定试验次数 (NumTrials) 以及每次试验的成功概率 (Prob),此函数返回最小成功次数 k,其中 k 次成功的累积概率大于或等于给定累积概率 (CumulativeProb)。
與 N 相關的反二項式 (invBinomN())
给定每次试验的成功概率 (Prob) 和成功次数 (NumSuccess),此函数返回最小试验次数 N,其中 x 次成功的累积概率小于或等于给定累积概率 (CumulativeProb)。
卜松機率密度函數 (Pdf) (poissPdf())
針對具有指定平均值 μ(必須是 >0 的實數)的離散卜松分佈,計算 x 的機率。x 可以是整數或整數的序列表。機率密度函數 (pdf) 為:
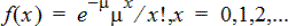
此分佈有助於用來判斷在開始一項試驗前,取得特定成功次數的機率。例如,您可以使用此計算來預測於拋八次錢幣當中,會發生正面的次數。
卜松累積分佈函數 (Cdf) (poissCdf())
以指定平均值 x 計算卜松離散分佈的累積機率。
此分佈有助於用來判斷在試驗的上下限之間,發生特定成功次數的機率。例如,您可利用此計算來預測從拋第3次到第8次硬幣中,顯示正面的次數。
幾何機率密度函數 (Pdf) (geomPdf())
針對具有指定成功機率 p,以計算發生第一次成功的試驗次數 x 的機率。0{p{1 必須為真。x 可以是整數或整數的序列表。機率密度函數 (pdf) 為:
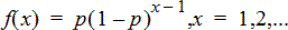
此分佈有助於用來判斷在獲得成功前,最可能需要的試驗次數。例如,您可以使用此計算來預測要拋幾次錢幣才會得到正面。
幾何累積分佈函數 (Cdf) (geomCdf())
計算從下限到上限的累積幾何機率(指定成功機率是 p)。
此分佈有助於用來判斷從第 1 次到第 n 次試驗期間,發生第一次成功的相關聯機率。例如,您可利用此計算來判斷在第 1 次、第 2 次、第 3 次、...、到第 n 次拋錢幣會顯示正面的機率。