È possibile eseguire calcoli statistici per analizzare dati. L'esempio seguente adatta un modello di regressione lineare y=mx+b a due liste nelle colonne A e B.

1.

Nel menu Statistica, selezionare Calcoli statistici > Regressione lineare (mx+b) per scegliere il modello di regressione.

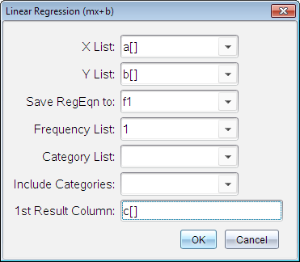
Viene visualizzata la finestra di dialogo Regressione lineare (mx+b).

2.

Digitare a[] come colonna per la Lista X.

3.

Digitare b[] come colonna per la Lista Y.

4.

Per memorizzare l'equazione di regressione in una variabile determinata, sostituire a Salva equazione di regressione in con il nome della variabile.

5.

Digitare c[] come colonna per 1° risultato.

6.

Fare clic su OK.

Foglio elettronico inserisce due colonne: una contenente i nomi dei risultati e una contenente i valori corrispondenti.

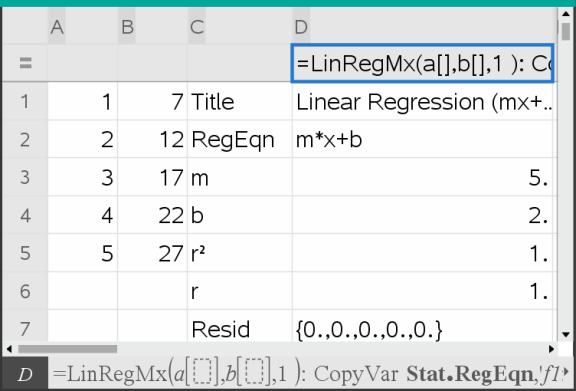
Nota: i risultati sono collegati ai dati sorgente. Ad esempio, se viene modificato un valore nella colonna A, l'equazione di regressione viene aggiornata automaticamente.

 

Foglio elettronico memorizza i risultati statistici utilizzando un nome di gruppo di variabili nel formato stat.nnn, dove nnn è il nome del risultato (ad esempio, stat.RegEqn e stat.Resid). L'uso di nomi standard per le variabili semplifica l'identificazione e il successivo impiego di variabili statistiche. Se si desidera utilizzare un nome di gruppo di variabili personalizzato invece del nome standard, è possibile modificare la formula nella cella della formula di colonna.

Si potrebbe utilizzare la seguente formula per memorizzare i risultati nel gruppo di variabili MystatsB.

=LinRegMx(a[],b[],1 ): CopyVar Stat., MystatsB.

Successivamente è possibile visualizzare i risultati inserendo la seguente espressione  nell'applicazione Calcolatrice o in un'altra colonna dell'applicazione Foglio elettronico:

MystatsB.results

 

Il menu Calcoli statistici consente di selezionare i calcoli illustrati sotto. Per ulteriori informazioni, consultare la Guida di riferimento TI-Nspire™  .

Statistiche a una variabile (OneVar)

Analizza dati con una variabile misurata. È possibile specificare una lista di frequenze opzionale. I dati statistici restituiti utilizzando questa tecnica di analisi sono:

•

Media del campione, x

•

Somma dei dati, Gx

•

Somma dei quadrati dei dati, Gx2

•

Deviazione standard del campione, sx

•

Deviazione standard della popolazione, sx

•

dimensione del campione, n

•

X-min

•

primo quartile, Q1

•

Mediana

•

terzo quartile, Q3

•

X-max

•

Somma dei quadrati delle deviazioni, SSx = G(x Nx)2

Statistiche a due variabili (TwoVar)

Analizza dati appaiati. Lista 1 è la variabile indipendente. Lista 2 è la variabile dipendente. È possibile specificare una lista di frequenze opzionale. I dati statistici restituiti utilizzando questa tecnica di analisi sono:

per ciascuna lista:

•

Media del campione, x o y

•

Somma dei dati, Gx o Gy

•

Somma dei quadrati dei dati, Gx2 o Gy2

•

deviazione standard del campione, sx = sn-1x o sy = sn-1y

•

deviazione standard della popolazione, sx = snx oppure sy = sny

•

X-min o Y-min

•

primo quartile, Q1X o Q1Y

•

Mediana

•

terzo quartile, Q3X or Q3Y

•

X-max o Y-max

•

Somma dei quadrati delle deviazioni, SSx = G(x Nx)2 o SSy = G(y Ny)2

Altri dati:

•

dimensione del campione per ciascun set di dati, n

•

Gxy

•

coefficiente di correlazione, R.

Regressione lineare (mx+b) (LinRegMx)

Approssima l'equazione del modello y=ax+b ai dati utilizzando un adattamento dei minimi quadrati. Visualizza valori per m (pendenza) e b (intercetta-y).

Regressione lineare (a+bx) (LinRegBx)

Approssima l'equazione del modello y=a+bx ai dati utilizzando un adattamento dei minimi quadrati. Visualizza valori per a (intercetta-y), b (pendenza), r2 e r.

Linea mediana-mediana (MedMed)

Approssima l'equazione del modello y=mx+b ai dati utilizzando la tecnica della linea mediana-mediana (linea di resistenza), calcolando i punti generici x1, y1, x2, y2, x3 e y3. -La linea mediana medianavisualizza valori per m (pendenza) e b (intercetta-y).

Regressione quadratica (QuadReg)

Adatta il polinomio di secondo grado y=ax2+bx+c ai dati. Visualizza valori per a, b, c e R2. Per tre punti, l'equazione è un adattamento polinomiale; per quattro o più punti è una regressione polinomiale. Sono necessari almeno tre punti.

Regressione cubica (CubicReg)

Approssima il polinomio di terzo grado y=ax3+bx2+cx+d ai dati Visualizza valori per a, b, c, d, e R2. Per quattro punti l'equazione è un adattamento polinomiale; per cinque o più punti è una regressione polinomiale. Sono necessari almeno quattro punti.

Regressione quartica (QuartReg)

Approssima il polinomio di quarto grado y=ax4+bx3+cx2+dx+e ai dati Visualizza valori per a, b, c, d, e, e R2. Per cinque punti l'equazione è un adattamento polinomiale; per sei o più punti è una regressione polinomiale. Sono necessari almeno cinque punti.

Regressione su potenza, (PowerReg)

Approssima l'equazione del modello y=axb ai dati utilizzando un adattamento dei minimi quadrati su valori trasformati ln(x) e ln(y). Visualizza valori per a, b, r2 e r.

Regressione esponenziale (ExpReg)

Approssima l'equazione del modello y=abx ai dati utilizzando un adattamento dei minimi quadrati su valori trasformati x e ln(y). Visualizza valori per a, b, r2 e r.

Regressione logaritmica (LogReg)

Approssima l'equazione del modello y=a+b ln(x) ai dati utilizzando un adattamento dei minimi quadrati su valori trasformati ln(x) e y. Visualizza valori per a, b, r2 e r.

Regressione sinusoidale (SinReg)

Approssima l'equazione del modello y=a sin(bx+c)+d ai dati utilizzando un adattamento iterativo dei minimi quadrati Visualizza valori per a, b, c e d. Sono necessari almeno quattro punti. Sono necessari almeno due punti per ciclo al fine di evitare false stime di frequenza.

Nota: l'output di SinReg è sempre espresso in radianti, indipendentemente dall'impostazione della modalità Radianti/Gradi.

Regressione logistica (d=0) (Logistic)

Approssima l'equazione del modello y=c/(1+a*e-bx) ai dati utilizzando un adattamento iterativo dei minimi quadrati. Visualizza valori per a, b e c.

Regressione logistica (dƒ0) (LogisticD)

Approssima l'equazione del modello y=c(1+a*e(-bx))+d ai dati utilizzando un adattamento iterativo dei minimi quadrati. Visualizza valori per a, b, c e d.

Regressione lineare multipla (MultReg)

Calcola la regressione lineare multipla della lista Y sulle liste X1, X2, …, X10.