Test statistici supportati
I test di ipotesi sono disponibili dall'applicazione Foglio elettronico. Per ulteriori informazioni su queste funzioni, vedere la Guida di riferimento TI-Nspire™.
Alcune procedure guidate dei test statistici visualizzano una casella di controllo Disegna. Per impostazione predefinita, la casella non è selezionata. Selezionandola si crea nella pagina un'area di lavoro di Dati e statistiche e vi si tracciano i risultati.
z test (zTest)
Esegue un test d'ipotesi su un'unica media non nota di una popolazione, m, quando la deviazione standard della popolazione, s, è nota. Viene verificata l'ipotesi nulla H0: m=m0 in contrapposizione a una delle alternative seguenti.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Questo test viene utilizzato per grandi popolazioni distribuite normalmente. La deviazione standard deve essere nota.
Questo test è utile per determinare se la differenza tra una media del campione e una media della popolazione è statisticamente significativa quando si conosce la deviazione reale di una popolazione.
t test (tTest)
Esegue una verifica dell'ipotesi su un'unica media m non nota di una popolazione quando la deviazione standard s della popolazione non è nota Viene verificata l'ipotesi nulla H0: m=m0 in contrapposizione a una delle alternative seguenti.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Questo test è simile a z Test, ma viene utilizzato quando la popolazione è piccola e distribuita normalmente. Questo test viene utilizzato con maggior frequenza di z Test perché in statistica si incontrano più facilmente popolazioni campione piccole anziché grandi.
Questo test è utile per determinare se due popolazioni normalmente distribuite hanno medie uguali oppure per determinare se una media del campione differisce da una media della popolazione in maniera significativa e la deviazione standard della popolazione non è nota.
Z Test su 2 campioni (zTest_2Samp)
Verifica la parità delle medie di due popolazioni (m1 e m2) basate su campioni indipendenti quando le deviazioni standard di entrambe le popolazioni (s1 e s2) sono note. Viene verificata l'ipotesi nulla H0: m1=m2 in contrapposizione a una delle alternative seguenti.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
t Test su 2 campioni (tTest_2Samp)
Verifica la parità delle medie di due popolazioni (m1 e m2) basate su campioni indipendenti quando nessuna delle deviazioni standard delle popolazioni (s1 o s2) è nota. Viene verificata l'ipotesi nulla H0: m1=m2 in contrapposizione a una delle alternative seguenti.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
z Test su 1 proporzione (zTest_1Prop)
Esegue una verifica su una proporzione (prop) di successi non nota Utilizza come input il numero di esiti favorevoli nel campione x e il numero di osservazioni nel campione n. 1-Prop z Test Verifica l'ipotesi nulla H0: prop=p0 in contrapposizione a una delle alternative seguenti.
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
Questo test è utile per determinare se la probabilità di successo vista nel campione è significativamente differente dalla probabilità della popolazione oppure se è dovuta a un errore di campionamento, deviazione o altri fattori.
z Test su 2 proporzioni (zTest_2Prop)
Esegue un test per confrontare la proporzione di successi (p1 e p2) di due popolazioni. Utilizza come input il numero di successi in ciascun campione (x1 e x2) e il numero di osservazioni in ciascun campione (n1 e n2). 2-Prop z Test Verifica l'ipotesi nulla H0: p1=p2 (utilizzando la proporzione del campione aggregata Ç) in contrapposizione a una delle alternative seguenti.
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
Questo test è utile per determinare se la probabilità di successo vista in due campioni è uguale.
c2GOF (c2GOF)
Esegue una verifica per confermare che i dati del campione appartengono a una popolazione conforme a una data distribuzione. Ad esempio, c2 GOF può confermare che i dati del campione provenivano da una distribuzione normale.
c2 test 2 dimensioni (c22 dimensioni)
Esegue un test chi quadrato per associazione sulla tabella a due dimensioni dei totali nella matrice Osservati specificata. L'ipotesi nulla H0 per una tabella a due dimensioni è: non esiste alcuna associazione tra variabili di riga e variabili di colonna. L'ipotesi alternativa è: le variabili sono in relazione tra loro.
2 campioni FTest (FTest_2campioni)
Esegue un test F-per comparare due deviazioni standard della popolazione (s1 e s2). Le medie e le deviazioni standard delle popolazioni sono tutte non note. 2-campioni FTest, che utilizza il rapporto di varianze del campione Sx12/Sx22, verifica l'ipotesi nulla H0: s1=s2 in contrapposizione a una delle alternative seguenti.
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
Di seguito viene fornita la definizione di 2-campioni FTest.
|
Sx1, Sx2 |
= |
Deviazioni standard dei campioni con n1N1 e n2N1 gradi di libertà gl, rispettivamente. |
|
|
|
Statistica F = |
|
df(x, n1N1, n2N1) |
= |
Fpdf( ) con gradi di libertà gl, n1N1 e n2N1 |
|
p |
= |
valore p riportato |
2-campioni FTest per l'ipotesi alternativa s1 > s2.
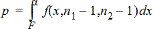
2-campioni FTest per l'ipotesi alternativa s1 < s2.
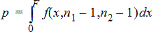
2-campioni FTest per l'ipotesi alternativa s1ƒs2. Gli estremi devono soddisfare quanto segue:
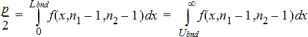
dove: [Lbnd,Ubnd]=estremo inferiore ed estremo superiore
La statistica F- viene utilizzata come estremo che produce l'integrale più piccolo. L'estremo rimanente viene selezionato per ottenere il rapporto di uguaglianza dell'integrale precedente.
t Test regressione lineare (LinRegtTest)
Calcola una regressione lineare sui dati assegnati e un t test sul valore della pendenza b e il coefficiente di correlazione r per l'equazione y=a+bx. Verifica l'ipotesi nulla H0: b=0 (in modo equivalente, r=0) in contrapposizione a una delle alternative seguenti.
| • | Ha: bƒ0 e rƒ0 |
| • | Ha: b<0 e r<0 |
| • | Ha: b>0 e r>0 |
Test regressioni multiple (MultRegTest)
Calcola una regressione lineare sui dati assegnati e fornisce la statistica della verifica F per la linearità.
Per ulteriori informazioni, consultare la Guida di riferimento TI-Nspire™.
ANOVA (ANOVA)
Esegue l'analisi a una dimensione della varianza per confrontare le medie di un numero di popolazioni compreso tra 2 e 20. La procedura di confronto di queste medie di ANOVA prevede l'analisi della varianza nei dati del campione. Viene verificata l'ipotesi nulla H0: m1=m2=...=mk in contrapposizione all'alternativa Ha: non tutti i valori m1...mk sono uguali.
La verifica ANOVA è un metodo per determinare se esiste una differenza significativa tra i gruppi se confrontata con la differenza che si produce in ciascun gruppo.
Questo test è utile per determinare se la variazione dei dati da campione a campione mostra un'influenza statisticamente significativa di qualche altro fattore oltre alla variazione stessa dei set di dati. Ad esempio, l'incaricato per gli acquisti degli imballaggi per una ditta di spedizione desidera valutare tre diversi produttori di imballaggi. Riceve tre campioni di imballaggi da tutti i fornitori. ANOVA può aiutarlo a determinare se le differenze tra ciascun gruppo di campioni sono significative rispetto alle differenze all'interno di ciascun gruppo di campioni.
ANOVA a 2 variabili (ANOVA2way)
Esegue l'analisi a due dimensioni della varianza per confrontare le medie di un numero di popolazioni compreso tra due e 20. Il riepilogo dei risultati è memorizzato nella variabile stat.results.
L'analisi ANOVA a due variabili della varianza esamina gli effetti di due variabili indipendenti e contribuisce a determinare se questi interagiscono con la variabile dipendente. (In pratica, se due variabili indipendenti interagiscono, il loro effetto combinato può essere maggiore o minore dalla somma degli impatti di ogni singola variabile).
Questo test è utile per valutare le differenze, in modo simile all'analisi ANOVA, ma con l'aggiunta di un'altra potenziale influenza. Per continuare con l'esempio degli imballaggi di ANOVA, ANOVA a due variabili potrebbe esaminare l'influenza del materiale degli imballaggi sulle differenze riscontrate.
Selezione di un'ipotesi alternativa (ƒ < >)
La maggior parte degli editor di statistica inferenziale per le verifiche delle ipotesi richiedono di selezionare una delle tre ipotesi alternative.
| • | La prima è un'ipotesi alternativa di tipo ƒ, come ad esempio mƒm0 per il z Test. |
| • | La seconda è un'<ipotesi alternativa, come ad esempio m1<m2 per il 2-campioni t Test. |
| • | La terza è un'>ipotesi alternativa di tipo, come ad esempio p1>p2 per il 2-Prop z Test. |
Per selezionare un'ipotesi alternativa, spostare il cursore sull'alternativa appropriata, quindi premere Invio.
Selezione dell'opzione Aggregata
L'opzione Aggregata (solo 2-Campioni t Test e 2-Campioni t Intervallo) specifica se le varianze devono essere aggregate per il calcolo.
| • | Selezionare No per non aggregare le varianze. Le varianze della popolazione possono essere disuguali. |
| • | Selezionare Sì per aggregare le varianze. Si assume che le varianze della popolazione siano uguali. |
Per selezionare l'opzione Aggregata, selezionare Sì dall'elenco a discesa
