Esempio: Calcolare una distribuzione per approssimare il modello di distribuzione Fdp normale.
| 1. | Fare clic sulla cella della formula di colonna (la seconda cella dall’alto) nella colonna A. |
| 2. | Fare clic su Statistiche > Distribuzioni > Fdp normale per scegliere il modello di distribuzione. |
Viene visualizzata la finestra di dialogo Fdp normale con i campi per l’inserimento o la selezione degli argomenti per il calcolo.
| 3. | Premere Tab secondo necessità per passare da un campo all’altro e completare ogni argomento. I valori possono essere digitati direttamente oppure selezionati dall’elenco a discesa. |
| - | Valore X: Fare clic sulla freccia dell’elenco a discesa per scegliere una lista dell’attività per fornire i valori x per il calcolo. |
| - | Mean (Media): Digitare un valore per la media oppure fare clic sulla freccia dell’elenco a discesa per selezionare una variabile che la contenga. |
| - | Deviazione standard: Digitare un valore per la deviazione standard oppure selezionare una variabile che la contenga. |
| 4. | Fare clic sulla casella Disegna per visualizzare la distribuzione tracciata in Dati e statistiche. |
Nota: l’opzione Disegna non è disponibile per tutte le distribuzioni.
| 5. | Fare clic su OK. |
Foglio elettronico inserisce due colonne: una contenente i nomi dei risultati e una contenente i valori corrispondenti. I risultati vengono tracciati in Dati e statistiche.
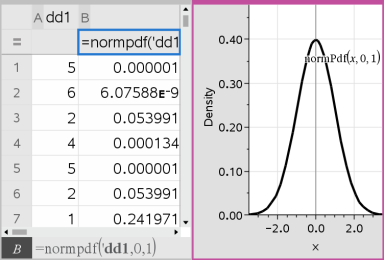
Nota: i risultati sono collegati ai dati sorgente. Ad esempio, se si cambia un valore nella colonna A, l’equazione viene automaticamente aggiornata.
Le seguenti distribuzioni sono disponibili dall’applicazione Foglio elettronico. Per ulteriori informazioni su queste funzioni, vedere la Guida di riferimento TI-Nspire™.
| • | Per ottenere un solo risultato della distribuzione sulla base di un solo valore, introdurre la funzione in un’unica cella. |
| • | Per ottenere una lista di risultati della distribuzione sulla base di una lista di valori, introdurre la funzione in una cella della formula di colonna. In questo caso, specificare una lista (colonna) che contenga valori. Per ciascun valore nella lista, la distribuzione restituisce un risultato corrispondente. |
Nota: per le funzioni di distribuzione che supportano l’opzione Disegna (normFDP, FDP t, χ² Fdp e F Fdp), tale opzione è disponibile solo se si inserisce la funzione di distribuzione in una cella della formula.
Fdp normale (normPdf)
Calcola la funzione della densità di probabilità (fdp) per la distribuzione normale in corrispondenza di un valore x specificato. I valori predefiniti sono media μ=0 e deviazione standard σ=1. La funzione della densità di probabilità (fdp) è:
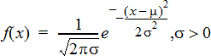
Questa distribuzione viene utilizzata per determinare la probabilità di occorrenza di un dato valore in una distribuzione normale. L’opzione Disegna è disponibile quando la funzione FDP normale viene attivata da una cella della formula.
Quando si accede a distribuzioni da una cella della formula, è necessario selezionare una lista valida dal menu a discesa onde evitare risultati inattesi. Se si accede da una cella, occorre specificare un numero per il valore x. La distribuzione restituisce la probabilità che si produca il valore specificato.
Fdr normale (normCdf)
Calcola la probabilità della distribuzione normale tra Estremo inferiore ed Estremo superiore per la media specificata, μ (default=0) e la deviazione standard, s (default=1). È possibile fare clic sulla casella Disegna (Area ombreggiatura) per ombreggiare l’area tra gli estremi inferiore e superiore. Modifiche dei valori iniziali di Estremo Inferiore ed Estremo Superiore aggiornano automaticamente la distribuzione.
Questa distribuzione è utile per determinare la probabilità di occorrenza di qualsiasi valore compreso tra gli estremi inferiore e superiore nella distribuzione normale. Equivale a calcolare l’area sotto la curva normale specificata tra gli estremi.
Normale inversa (invNorm)
Calcola la funzione della distribuzione normale cumulata inversa per una data area sotto la curva della distribuzione normale specificata da media, μ, e deviazione standard, s.
Questa distribuzione è utile per determinare il valore x dei dati nell’area da 0 a x<1 quando il percentile è noto.
Fdp t (Fdpt)
Calcola la funzione di densità di probabilità (fdp) per la distribuzione t a un valore x specificato. gl (gradi di libertà) deve essere > 0. La funzione della densità di probabilità (Fdp) è:
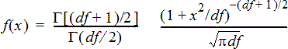
Questa distribuzione è utile per determinare la probabilità di occorrenza di un valore quando la deviazione standard della popolazione non è nota e la dimensione del campione è piccola. L’opzione Disegna è disponibile quando la funzione Fdp t viene attivata da una cella della formula.
Fdr t (Fdrt)
Calcola la probabilità di distribuzione t di Student tra Estremo inferiore ed Estremo superiore per i gl (gradi di libertà) specificati. È possibile fare clic sulla casella Disegna - Area ombreggiatura per ombreggiare l’area tra gli estremi. Modifiche dei valori iniziali di Estremo Inferiore ed Estremo Superiore aggiornano automaticamente la distribuzione.
Questa distribuzione è utile per determinare la probabilità di occorrenza di un valore all’interno di un intervallo definito dagli estremi inferiore e superiore di una popolazione normalmente distribuita quando la deviazione standard della popolazione non è nota.
t inversa (invt)
Calcola la funzione della probabilità di distribuzione-t cumulata inversa specificata dal grado di libertà, gl, per una data area sottesa dalla curva.
Questa distribuzione è utile per determinare la probabilità di occorrenza di dati nell’area da 0 a x<1. Questa funzione viene utilizzata quando la media della popolazione e/o la deviazione standard della popolazione non è nota.
c2 Fdp (c2 Fdp())
Calcola la funzione di densità di probabilità (fdp) per la distribuzione c2 (chi-quadro) a un valore x specificato. gl (gradi di libertà) deve essere un numero intero > 0. La funzione della densità di probabilità (Fdp) è:
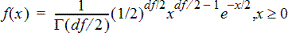
Questa distribuzione è utile per determinare la probabilità di occorrenza di un dato valore da una popolazione con una distribuzione c2. L’opzione Disegna è disponibile quando la funzione c2 Fdp viene attivata da una cella della formula.
c2 Fdr (c2 Fdr())
Calcola la probabilità della distribuzione c2 (chi-quadro) tra Estremo inferiore ed Estremo superiore per i gl (gradi di libertà) specificati. È possibile fare clic sulla casella Disegna - Area ombreggiatura per ombreggiare l’area tra gli estremi inferiore e superiore. Modifiche dei valori iniziali di Estremo inferiore e Estremo superiore aggiornano automaticamente la distribuzione.
Questa distribuzione è utile per determinare la probabilità di occorrenza di un valore all’interno degli estremi specificati di una popolazione con una distribuzione c2.
F Fdp (F Fdp())
Calcola la funzione di densità di probabilità (fdp) per la distribuzione F a un valore x specificato. gl (gradi di libertà) numeratore e gl denominatore devono essere numeri interi > 0. La funzione della densità di probabilità (Fdp) è:
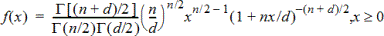
|
dove |
n = gradi di libertà del numeratore |
Questa distribuzione è utile per determinare la probabilità di due campioni di avere la medesima varianza. L’opzione Disegna è disponibile quando la funzione F Fdp viene attivata da una cella della formula.
F Fdr (F Fdr())
Calcola la probabilità della distribuzione F tra Estremo inferioreed Estremo superiore per il glNumer (gl, gradi di libertà) e glDenom specificati. È possibile fare clic sulla casella Disegna (Area ombreggiatura) per ombreggiare l’area tra gli estremi inferiore e superiore. Modifiche dei valori iniziali di Estremo inferiore e Estremo superiore aggiornano automaticamente la distribuzione.
Questa distribuzione è utile per determinare la probabilità che una singola osservazione rientri nell’intervallo compreso tra Estremo Inferiore e Estremo Superiore.
Fdr binomiale (binomPdf())
Calcola una probabilità in corrispondenza di x per la distribuzione binomiale discreta con il numero di prove e la probabilità di successo (p) specificati per ogni prova. Il parametro x può essere un numero intero o una lista di numeri interi. 0{p{1 deve essere vero. numero di prove deve essere un numero intero > 0. Se non si specifica x, viene restituita una lista di probabilità da 0 a numero di prove. La funzione della densità di probabilità (Fdp) è:
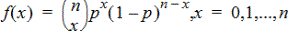
dove n = numero di prove
Questa distribuzione è utile per determinare la probabilità di successo in una prova del tipo "testa o croce", al lancio n. Ad esempio, si potrebbe usare questa distribuzione per predire la probabilità che esca "testa" al quinto lancio di "testa o croce".
Fdr binomiale (binomCdf())
Calcola la probabilità cumulata per la distribuzione binomiale discreta con il numero di prove n e le probabilità di successo p per ciascuna prova.
Questa distribuzione è utile per determinare la probabilità di successo in una prova prima che tutte le prove siano completate. Ad esempio, se è uscito testa e si pianifica di giocare 10 lanci di testa o croce, questa distribuzione predirebbe la possibilità di ottenere testa almeno una volta ogni 10 lanci.
Binomiale inverso (invBinom())
Dato il numero di tentativi (NumTrials) e la probabilità di successo di ogni tentativo (Prob), questa funzione restituisce il numero minimo di successi k, in modo che la probabilità cumulativa di successi k sia maggiore o uguale alla probabilità cumulativa (CumulativeProb) data.
Binomiale inverso rispetto a N (invBinomN())
Data la probabilità di successo di ogni tentativo (Prob) e il numero di successi (NumSuccess), questa funzione restituisce il numero minimo di tentativi N, in modo che la probabilità cumulativa di successi x sia minore o uguale alla probabilità cumulativa (CumulativeProb) data.
Fdp Poisson (poissPdf())
Calcola la probabilità in corrispondenza di x per la distribuzione discreta di Poisson con la media specificata, μ, che deve essere un numero reale > 0. x può essere un numero intero o una lista di numeri interi. La funzione della densità di probabilità (Fdp) è:
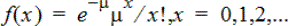
Questa distribuzione è utile per determinare la probabilità di ottenere un certo numero di esiti favorevoli prima che inizi la prova. Ad esempio, si potrebbe usare questo calcolo per prevedere quante volte uscirà "testa" in otto lanci di "testa o croce".
Fdr Poisson (poissFdr())
Calcola la probabilità cumulata per la distribuzione discreta di Poisson con la media x specificata.
Questa distribuzione è utile per determinare la probabilità che si verifichi un certo numero di esiti favorevoli tra gli estremi superiore e inferiore di una prova. Ad esempio, si potrebbe usare questo calcolo per prevedere quante volte uscirà "testa" tra il lancio n. 3 e il lancio n. 8 di "testa o croce".
Fdp geometrico (geomFdp())
Calcola una probabilità in corrispondenza di x, il numero della prova in cui si è verificato il primo caso favorevole, per la distribuzione geometrica discreta con la probabilità di esiti favorevoli p specificata. 0{p{1 deve essere vero. x può essere un numero intero o una lista di numeri interi. La funzione della densità di probabilità (fdp) è:
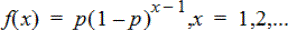
Questa distribuzione è utile per determinare il numero più probabile di prove prima di ottenere un esito positivo. Ad esempio, si potrebbe usare questo calcolo per prevedere il numero di lanci di "testa o croce" da giocare prima di ottenere "testa".
Fdr geometrico (geomFdr())
Calcola una probabilità geometrica cumulata da Estremo inferiore a Estremo superiore con la probabilità di esiti favorevoli p specificata.
Questa distribuzione è utile per determinare la probabilità associata al primo esito favorevole che si verifica durante le prove da 1 a n. Ad esempio, si potrebbe usare questo calcolo per determinare la probabilità che esca "testa" al lancio 1, 2, 3, ..., n.