Du kan udføre statistiske beregninger til analyse af data. Følgende eksempel tilpasser en lineær regressionsmodel y=mx+b til de to lister i søjle A og B:
| 1. | Åbn menuen Statistik, vælg Statistisk beregning > og vælg Lineær regression (mx+b) for at vælge regressionsmodellen. |
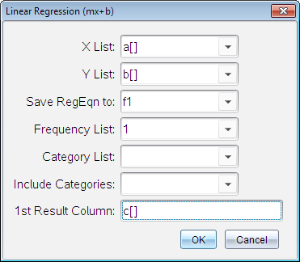
Dialogboksen Lineær regression (mx+b) åbnes.
| 2. | Indtast a[]som søjlen for X-listen. |
| 3. | Indtast b[]som søjlen for Y-listen. |
| 4. | Hvis du vil lagre regressionsligningen i en navngivet funktion, skal du erstatte Gem RegEqn i med navnet på funktionen. |
| 5. | Skriv c[] som søjlebogstav for det første resultat. |
| 6. | Klik på OK. |
Lister & regneark indsætter to søjler; en med navnene på resultaterne og en med de tilsvarende værdier.
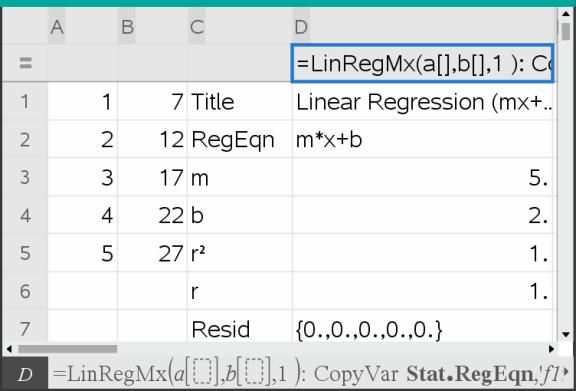
Bemærk: Resultaterne er linket til kildedataene. Hvis du eksempelvis ændrer en værdi i søjle A, opdateres regressionsligningen automatisk.
Lister og Regneark gemmer statistiske resultater under et variabelgruppenavn i formatet stat.nnn, hvor nnn er resultatnavnet (for eksempel, stat.RegEqn og stat.Resid). Anvendelsen af standardnavne til variabler gør det nemmere at identificere og bruge de statistiske variabler senere. Hvis du vil bruge en brugerdefineret variabelgruppe i stedet for standardnavnet, kan du redigere formlen i formelcellen.
Du kan fx vælge at bruge følgende formel til at lagre resultaterne i variabelgruppen MystatsB.
=LinRegMx(a[],b[],1 ): CopyVar Stat., MystatsB.
Senere kan du se resultaterne ved at indtaste følgende udtryk i Beregninger- eller Noter-applikationen eller i en anden søjle i applikationen Lister og Regneark:
MystatsB.results
Med menuen Statistiske beregninger kan du vælge mellem beregningerne beskrevet nedenfor. For yderligere information henvises der til Vejledningen-til TI Nspire™.
Statistik med én variabel (OneVar)
Analyserer data med én målt variabel. Du kan angive en valgfri antalsliste. De statistiske data, der returneres med denne analyseteknik, er:
| • | Middelværdi for stikprøve, x |
| • | Sum af data, Gx |
| • | Sum af kvadratet på data, Gx2 |
| • | Standardafvigelse for stikprøve, sx |
| • | Populations standardafvigelse, sx |
| • | Stikprøvestørrelse, n |
| • | X-min |
| • | Første kvartil, Q1 |
| • | Median |
| • | Tredje kvartil, Q3 |
| • | X-maks |
| • | Sum af kvadratet på afvigelser, SSx = G(x Nx)2 |
Statistik med to variable (ToVar)
Analyserer parrede data. Liste 1 er den uafhængige variabel. Liste 2 er den afhængige variabel. Du kan angive en valgfri antalsliste. De statistiske data, der returneres med denne analyseteknik, er:
For hver liste:
| • | Middelværdi for stikprøve, x eller y |
| • | Sum af data, Gx eller Gy |
| • | Sum af kvadratet på data, Gx2 eller Gy2 |
| • | Standardafvigelse for stikprøve, sx = sn-1x eller sy = sn-1y |
| • | Populationsstandardafvigelse, sx = snx eller sy = sny |
| • | X-min eller Y-min |
| • | Første kvartil, Q1X eller Q1Y |
| • | Median |
| • | Tredje kvartil, Q3X eller Q3Y |
| • | X-maks eller Y-maks |
| • | Sum af kvadratet på afvigelser, SSx = G(x Nx)2 eller SSy = G(y Ny)2 |
Yderligere data:
| • | Stikprøvestørrelse for hvert datasæt, n |
| • | Gxy |
| • | Korrelationskoefficient, R. |
Lineær regression (mx+b) (LinRegMx)
Tilpasser ligningsmodellen y=ax+b til data med metoden for mindste kvadrater. Den viser værdier for m (hældning) og b (y-skæring).
Lineær regression (a+bx) (LinRegBx)
Tilpasser ligningsmodellen y=a+bx til data med metoden for mindste kvadrater. Den viser værdier for a (y-skæring), b (hældning), r2 og r.
Median-medianlinje (MedMed)
Tilpasser modelligningen y=mx+b til dataene med teknikken median-medianlinjen (resistent linje) og beregner punkterne x1, y1, x2, y2, x3 og y3. Median-medianlinje viser værdierne for m (hældning) og b (y-skæring).
Andengradsregression (QuadReg)
Tilpasser andengradspolynomiet y=ax2+bx+c til dataene. Den viser værdier for a, b, c og R2. For tre datapunkter er ligningen et præcist polynomium; for fire eller derover er den et regressionspolynomium. Mindst tre datapunkter er påkrævet.
Tredjegradsregression (CubicReg)
Tilpasser tredjegradspolynomiet y=ax3+bx2+cx+d til dataene. Den viser værdier for a, b, c, d og R2. For fire datapunkter er ligningen et præcist polynomium; for fem eller derover er den et regressionspolynomium. Mindst fire punkter er påkrævet.
Fjerdegradsregression (QuartReg)
Tilpasser fjerdegradspolynomiet y=ax4+bx3+cx2+dx+e til dataene. Den viser værdier for a, b, c, d, e og R2. For fem datapunkter er ligningen et præcist polynomium; for seks eller derover er den et regressionspolynomium. Mindst fem punkter er påkrævet.
Potensregression (PowerReg)
Tilpasser modelligningen y=axb til data med metoden for mindste kvadrater tilpasset de transformerede værdier ln(x) og ln(y). Den viser værdier a, b, r2 og r.
Eksponentiel regression (ExpReg)
Tilpasser modelligningen y=abx til data med metoden for mindste kvadrater tilpasset de transformerede værdier x og ln(y). Den viser værdier a, b, r2 og r.
Logaritmisk regression (LogReg)
Tilpasser modelligningen y=a+b ln(x) til data med metoden for mindste kvadrater tilpasset de transformerede værdier ln(x) and y. Den viser værdier a, b, r2 og r.
Sinusregression (SinReg)
Tilpasser ligningsmodellen y=a sin(bx+c)+d til data med en iterativ mindste kvadraters metode. Den viser værdier for a, b, c og d. Mindst fire datapunkter er påkrævet. Mindst to datapunkter pr. svingning er påkrævet for at undgå skæve estimater for frekvens.
Bemærk: Output af SinReg er altid i radianer, uanset indstillingen for Radian/Grader.
Logistisk regression (d=0) (Logistic)
Tilpasser ligningsmodellen y=c/(1+a*e-bx) til dataene med en iterativ mindste kvadraters metode. Den viser værdier for a, b og c.
Logistisk regression (dƒ0) (LogisticD)
Tilpasser ligningsmodellen y=c(1+a*e(-bx))+d til dataene med en iterativ mindste kvadraters metode. Den viser værdier for a, b, c og d.
Multipel lineær regression (MultReg)
Beregner den multiple lineære regression af liste Y som funktion af listerne X1, X2, …, X10.