Eksempel: Beregn en fordeling, der passer til Normal pdf-fordelingsmodellen.
| 1. | Vælg formelcellen (næstøverste celle) i kolonne A. |
| 2. | Klik på Statistik > Fordelinger > Normal Pdf for at vælge fordelingsmodellen. |
Dialogboksen Normal Pdf åbnes og viser felter til skrivning og valg af argumenterne for beregningen.
| 3. | Tryk på Tab efter behov for at navigere mellem felterne og angive de enkelte argumenter. Du kan indtaste værdier eller vælge dem fra rullelisten: |
| - | X-værdi: Klik på rullegardinpilen for at vælge en liste i opgaven for at give x-værdierne til beregningen. |
| - | Middelværdi: Skriv en værdi for middelværdien, eller klik på rullegardinpilen for at vælge en variabel med middelværdien. |
| - | Standardafvigelse: Skriv en værdi for standardafvigelsen, eller vælg en variabel, der indeholder standardafvigelsen. |
| 4. | Klik i afkrydsningsfeltet Tegn for at se fordelingen plottet i Data og statistik. |
Bemærk: Funktionen Tegn er ikke tilgængelig for alle fordelinger.
| 5. | Klik på OK. |
Lister og regneark indsætter to kolonner: en med navnene på resultaterne og en med de tilsvarende værdier. Resultaterne plottes i Data og statistik.
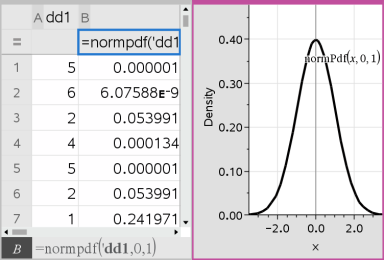
Bemærk: Resultaterne er linket til kildedataene. Du kan for eksempel ændre en værdi i kolonne A, og beregningen opdateres automatisk.
Følgende fordelinger er tilgængelige i applikationen Lister og regneark. Du kan finde flere oplysninger om disse værktøjer i opslagsvejledningen til TI-Nspire™.
| • | For at frembringe et enkelt resultat fra fordelingen baseret på en enkelt værdi, skal du indtaste funktionen i en enkelt celle. |
| • | For at frembringe en liste af resultater fra fordelingen baseret på en liste af værdier, skal du indtaste funktionen i kolonnens formelcelle. I dette tilfælde angiver du en liste (kolonne), der indeholder værdier. For hver værdi i listen returnerer fordelingen et tilsvarende resultat. |
Bemærk: For fordelingsfunktioner, der understøtter tegnefunktionen (normPDF, t PDF, χ² Pdf og F Pdf), er funktionen kun tilgængelig, hvis du indsætter fordelingen i en formelcelle.
Normal Pdf (normPdf)
Beregner sandsynlighedstætheden (pdf) for normalfordelingen ved en bestemt x-værdi. Standardindstillingerne er middelværdi μ=0 og standardafvigelse σ=1 . Sandsynlighedsfunktionen (pdf) er:
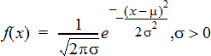
Fordelingen anvendes til at bestemme sandsynlighedstætheden for, at en bestemt værdi forekommer i en normalfordeling. Tegnefunktionen er tilgængelig, når Normal Pdf kaldes fra en formelcelle.
Når du åbner fordelinger fra formelcellen, skal du vælge en gyldig liste i rullemenuen for at undgå utilsigtede resultater. Hvis den åbnes fra en celle, skal du angive et tal for x-værdien. Fordelingen returnerer sandsynligheden for, at den angivne værdi vil forekomme.
Normal Cdf (normCdf)
Beregner normalfordelingssandsynligheden mellem nedre grænse og øvre grænse for den angivne middelværdi, μ (standard=0) og standardafvigelsen, s (standard=1). Du kan klikke på afkrydsningsfeltet Tegn (Skraver område) for at skravere området mellem øvre og nedre grænse. Ændringer i nedre grænse og øvre grænse opdaterer automatisk fordelingen.
Fordelingen er nyttig til at bestemme sandsynligheden for, at en vilkårlig værdi forekommer mellem de øvre og nedre grænser i en normalfordeling. Det svarer til at beregne arealet under den angivne normalfordelingskurve mellem afgrænsningerne.
Invers normal (invNorm)
Beregner den inverse kumulerede normalfordelingsfunktion for et givet areal under normalfordelingskurven specificeret af middelværdi, μ, og standardafvigelse, s.
Fordelingen er nyttig til at bestemme x-værdien af data i området fra 0 til x<1, når procentdelen kendes.
t Pdf (tPdf)
Beregner sandsynlighedstætheden (pdf) for t-fordelingen ved en angivet x-værdi. fg (frihedsgrader) skal være > 0. Sandsynlighedsfunktionen (pdf) er:
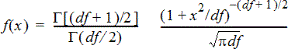
Fordelingen er nyttig til at bestemme sandsynlighedstætheden for, at en værdi forekommer, når populationsstandardafvigelsen ikke er kendt, og stikprøvestørrelsen er lille. Tegnefunktionen er tilgængelig, når t Pdf beregnes ud fra en formelcelle.
t Cdf (tCdf)
Beregner student-t fordelingssandsynligheden mellem nedre grænse og øvre grænse for de angivne fg (frihedsgrader). Du kan klikke på afkrydsningsfeltet Tegn (skraver område) for at skravere området mellem grænserne. Ændringer i nedre grænse og øvre grænse opdaterer automatisk fordelingen.
Fordelingen er nyttig til at bestemme sandsynligheden for, at en værdi forekommer inden for et interval defineret af den nedre og øvre grænse for en normalfordelt population, når populationsstandardafvigelsen ikke er kendt.
Invers t (invt)
Beregner den inverse kumulative t-fordeling, der hører til frihedsgraden df, for et givet areal under kurven.
Fordelingen er nyttig til at bestemme sandsynligheden for, at data forekommer i området fra 0 til x<1. Denne funktion anvendes, når populationsmiddelværdi og/eller populationsstandardafvigelsen ikke kendes.
c2 Pdf (c2 Pdf())
Beregner sandsynlighedstætheden (pdf) for c2 (chi-kvadrat)-fordelingen ved en specificeret x-værdi. fg (frihedsgrader) skal være et heltal > 0. Sandsynlighedsfunktionen (pdf) er:
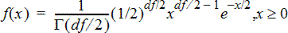
Fordelingen er nyttig til at bestemme sandsynlighedstætheden for, at en given værdi forekommer i en population med en c2-fordeling. Tegnefunktionen er tilgængelig, når c2 Pdf beregnes ud fra en formelcelle.
c2 Cdf (c2 Cdf())
Beregner c2 (chi-kvadrat)-sandsynlighedsfordelingen mellem nedre grænse og øvre grænse for de angivne fg (frihedsgrader). Du kan klikke på afkrydsningsfeltet Tegn skraveret område for at skravere området mellem øvre og nedre grænse. Ændringer i nedre grænse og øvre grænse opdaterer automatisk sandsynlighedsfordelingen.
Fordelingen er nyttig til at bestemme sandsynligheden for, at en værdi forekommer mellem de givne grænser for en population med en c2 -fordeling.
F Pdf (F Pdf())
Beregner sandsynlighedstætheden (pdf) for F-fordelingen ved en specificeret x-værdi. Tæller df (frihedsgrader) og nævner fg skal være heltal > 0. Sandsynlighedsfunktionen (pdf) er:
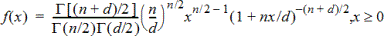
|
hvor |
n = tællerens frihedsgrader |
Fordelingen er nyttig til at bestemme sandsynligheden for, at to stikprøver har samme varians. Tegnefunktionen er tilgængelig, når F Pdf beregnes ud fra en formelcelle.
F Cdf (F Cdf())
Beregner F-fordelingssandsynligheden mellem nedre grænse og øvre grænse for den angivne Tæller (frihedsgrader) og Nævner. Du kan klikke på afkrydsningsfeltet Tegn (Skraver område) for at skravere området mellem øvre og nedre grænse. Ændringer i nedre grænse og øvre grænse opdaterer automatisk sandsynlighedsfordelingen.
Fordelingen er nyttig til at bestemme sandsynligheden for, at en enkelt observation falder inden for området mellem nedre grænse og øvre grænse.
Binomial Pdf (binomPdf())
Beregner en sandsynlighed på x for den diskrete binomialfordeling med de angivne antalforsøg og sandsynligheden for succes (p) for hvert forsøg. Parameteren x kan være et heltal eller en liste med heltal. 0{p{1 skal være opfyldt. antal forsøg skal være et heltal > 0. Hvis du ikke angiver x, returneres en liste med sandsynligheder fra 0 til antalforsøg. Sandsynlighedsfunktionen (pdf) er:
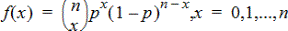
hvor n = antalforsøg
Fordelingen er nyttig til at bestemme sandsynligheden for succes i et succes/fejl-forsøg ved forsøg n. Du kan for eksempel anvende fordelingen til at bestemme sandsynligheden for at få én krone i fem forsøg, når du slår plat og krone.
Binomial Cdf (binomCdf())
Beregner en kumulativ sandsynlighed for den diskrete binomialfordeling med n forsøg og sandsynligheden p for succes ved hvert forsøg.
Fordelingen er nyttig til at bestemme sandsynligheden for et antal succeser i en forsøgsrække, før alle forsøg er gennemført. Hvis det for eksempel defineres som en succes at slå krone, og du vil slå plat og krone 10 gange, kan denne fordeling forudsige chancen for at få krone mindst en gang i de 10 forsøg.
Invers binomial (invBinom())
Givet antallet af forsøg (NumTrials) og sandsynligheden for succes i hvert forsøg (Prob) vil denne funktion returnere det minimale antal successer, k, således at den kumulerede sandsynlighed for k succeser er større end eller lig med den givne kumulerede sandsynlighed (CumulativeProb).
Invers binomial med hensyn til N (invBinomN())
Givet sandsynligheden for succes i hvert forsøg (Prob) og antallet af succeser (NumSuccess) vil denne funktion returnere det minimale antal forsøg, N, således at den kumulerede sandsynlighed for x succeser er mindre end eller lig med den givne kumulerede sandsynlighed (CumulativeProb).
Poisson Pdf (poissPdf())
Beregner en sandsynlighed på x for den diskrete Poisson-fordeling med den angivne middelværdi, μ, som skal være et reelt tal > 0. x kan være et heltal eller en liste af heltal. Sandsynlighedsfunktionen (pdf) er:
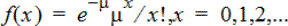
Fordelingen er nyttig til at bestemme sandsynligheden for at opnå et bestemt antal succeser, før en forsøgsrække begynder. Du kan for eksempel anvende denne til at forudsige antallet af gange, du får krone, når du slår plat og krone 8 gange.
Poisson Cdf (poissCdf())
Beregner en kumulativ sandsynlighed for den diskrete poisson-fordeling med en angivet middelværdi x.
Fordelingen er nyttig til at bestemme sandsynligheden, for at et bestemt antal succeser forekommer mellem et forsøgs øvre og nedre grænser. Du kan for eksempel anvende beregningen til at forudsige det antal gange, du slår krone, mellem forsøg nr. 3 og forsøg nr. 8.
Geometrisk Pdf (geomPdf())
Beregner en sandsynlighed på x, nummeret på det forsøg, hvor den første succes forekommer, ud fra den diskrete geometriske fordeling med den angivne sandsynlighed for succes p. 0{p{1 skal være sandt. x kan være et heltal eller en liste af heltal. Sandsynlighedsfunktionen (pdf) er:
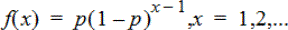
Fordelingen er nyttig til at finde det mest sandsynlige antal forsøg, før der opnås succes. Du kan for eksempel anvende beregningen til at forudsige antallet af gange, du skal slå plat og krone, før du får krone.
Geometrisk Cdf (geomCdf())
Beregner en kumulativ geometrisk sandsynlighed fra nedre grænse til øvre grænse med den angivne sandsynlighed for succes, p.
Fordelingen er nyttig til at bestemme sandsynligheden for, at den første succes indtræffer mellem forsøg 1 og n. Du kan for eksempel anvende beregningen til at bestemme sandsynligheden for krone i forsøg nr. 1, nr. 2, nr. 3, ..., nr. n.