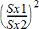Understøttede statistiske tests
Hypotesetests er tilgængelige i applikationen Lister og Regneark. Du kan finde flere oplysninger om disse værktøjer i opslagsvejledningen til TI-Nspire™.
Nogle af guiderne for Statistiske tests viser afkrydsningsfeltet Tegn. Som standard er feltet ikke afkrydset. Afkrydsning af dette felt opretter et Diagrammer og statistik-arbejdsområde på siden og tegner resultaterne i det pågældende arbejdsområde.
z test for én middelværdi (zTest)
Udfører en hypotesetest for et enkelt ukendt populationsgennemsnit, m, når populationens standardafvigelse, s, kendes. Den tester nulhypotesen H0: m=m0 mod et af nedenstående alternativer.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Testen anvendes til store populationer, der er normalfordelte. Standardafvigelsen skal være kendt.
Testen kan for eksempel anvendes til at bestemme, om differensen mellem en stikprøvemiddelværdi og en populationsmiddelværdi er statistisk signifikant, når du kender den faktiske standardafvigelse for en population.
t test for én middelværdi (tTest)
Udfører en hypotesetest for en enkelt ukendt populationsmiddelværdi m, når populationens standardafvigelse, s, er ukendt. Den tester nulhypotesen H0: m=m0 mod et af nedenstående alternativer.
| • | Ha: mƒm0 |
| • | Ha: m<m0 |
| • | Ha: m>m0 |
Testen er magen til en z-test for én middelværdi, men anvendes, når populationen er lille og normalfordelt. Testen anvendes hyppigere end z-testen, fordi små prøvepopulationer forekommer hyppigere i statistikken end de store.
Testen anvendes for eksempel til at bestemme, om to normalfordelte populationer har samme middelværdi, eller når du vil bestemme, om en stikprøvemiddelværdi er signifikant forskellig fra en populationsmiddelværdi, og populationens standardafvigelse er ukendt.
z-test for to middelværdier (zTest_2Samp)
Tester om to populationers middelværdier (m1 og m2) er identiske baseret på uafhængige stikprøver, når begge populationers standardafvigelse (s1 og s2) er kendt. Nulhypotesen H0: m1=m2 testes mod et af nedenstående alternativer.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
t-test for to middelværdier (tTest_2Samp)
Tester om to populationers middelværdier (m1 and m2) er identiske baseret på uafhængige stikprøver, når ingen af populationens standardafvigelser (s1 eller s2) er kendte. Nulhypotesen H0: m1=m2 testes mod et af nedenstående alternativer.
| • | Ha: m1ƒm2 |
| • | Ha: m1<m2 |
| • | Ha: m1>m2 |
z-test for én andel (zTest_1Prop)
Udfører en test for en ukendt andel af succeser (prop). Som input tager den antallet af succeser i stikprøven x og antallet af observationer i stikprøven n. -z-test for én andel tester nulhypotesen H0: prop=p0 mod et af nedenstående alternativer.
| • | Ha: propƒp0 |
| • | Ha: prop<p0 |
| • | Ha: prop>p0 |
Testen anvendes til at bestemme, om sandsynligheden for succes i en stikprøve er signifikant forskellig fra populationssandsynligheden, eller om det skyldes stikprøvefejl, afvigelse eller andre faktorer.
z-test for to andele (zTest_2Prop)
Udfører en test til at sammenligne andelen af succeser (p1 and p2) i to populationer. Som input bruger den antallet af succeser i hver stikprøve (x1 and x2) og antallet af observationer i hver stikprøve (n1 and n2). -z-test for to andele tester nulhypotesen H0: p1=p2 (med den kombinerede stikprøveandel Ç) mod et af nedenstående alternativer.
| • | Ha: p1ƒp2 |
| • | Ha: p1<p2 |
| • | Ha: p1>p2 |
Testen anvendes til at bestemme, om sandsynligheden for succes fundet i to stikprøver er den samme.
c2GOF (c2GOF)
Udfører en test for at bekræfte, om stikprøvedataene er fra en population, der er i overensstemmelse med en foreskrevet fordeling. For eksempel kan c2 GOF bekræfte, at stikprøvedataene kom fra en normalfordeling.
c2 uafhængighedstest (c22-way)
Udfører en chi-kvadrat-test for uafhængighed i en krydstabel for de angivne Observerede værdier. Nulhypotesen H0 for en uafhængighedstest er: der findes ingen sammenhæng mellem række- og søjlevariabler. Den alternative hypotese er: variablerne er indbyrdes afhængige.
F-test for to spredninger (FTest_2Samp)
Udfører en F-test for at sammenligne to normalfordelte populationers spredninger (s1 og s2). Populationsmiddelværdierne og standardafvigelserne er alle ukendte. F-test for tospredninger, som bruger forholdet mellem stikprøvevarianserne Sx12/Sx22, tester nulhypotesen H0: s1=s2 mod et af nedenstående alternativer.
| • | Ha: s1ƒs2 |
| • | Ha: s1<s2 |
| • | Ha: s1>s2 |
Nedenfor findes definitionen for F-test for tospredninger.
|
Sx1, Sx2 |
= |
Stikprøvestandardafvigelser på henholdsvis n1N1 og n2N1 frihedsgrad fg. |
|
|
|
F-statistik = |
|
fg(x, n1N1, n2N1) |
= |
Fpdf( ) med frihedsgrader fg, n1N1, og n2N1 |
|
p |
= |
rapporteret p-værdi |
F-test for tospredninger for den alternative hypotese s1 > s2.
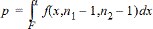
F-test for tospredninger for den alternative hypotese s1 < s2.
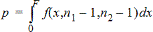
F-test for tospredninger for den alternative hypotese s1ƒs2. Grænserne skal opfylde følgende:
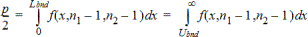
hvor: [Lbnd,Ubnd]=nedre og øvre grænse
F-statistikken anvendes for den grænse, der giver det mindste integral. Den anden grænse vælges, så der opnås lighed mellem integralerne.
Lineær regressions t-test (LinRegtTest)
Beregner en lineær regression ud fra de givne data og en t-test for hældningsværdien b og korrelationskoefficenten r for ligningen y=a+bx. Den tester nulhypotesen H0: b=0 (svarende til, r=0) mod et af nedenstående alternativer.
| • | Ha: bƒ0 og rƒ0 |
| • | Ha: b<0 og r<0 |
| • | Ha: b>0 og r>0 |
Multipel lineær regressionstest (MultRegTest)
Beregner en lineær regression på de givne data og leverer F-teststatistikken for linearitet.
For yderligere information henvises der til vejledningen til TI-Nspire™.
ANOVA (ANOVA)
Beregner en afhængig variansanalyse til at sammenligne middelværdierne for 2 til 20 populationer. ANOVA-proceduren til sammenligning af disse middelværdier inkluderer analyse af stikprøvedataenes variation. Nulhypotesen H0: m1=m2=...=mk testes mod den alternative Ha: Ikke alle m1...mk er lige store.
ANOVA-testen er en metode til at bestemme, om der er en signifikant forskel mellem grupperne, sammenlignet med forskellene indenfor hver gruppe.
Testen anvendes til at bestemme, om datavariationen fra stikprøve til stikprøve viser en statistisk signifikant indflydelse af en anden faktor end variationen inden for selve datasættene. For eksempel vil en kasseindkøber fra et shippingfirma undersøge tre forskellige kasseproducenter. Han skaffer prøvekasser fra alle tre leverandører. ANOVA kan hjælpe ham med at bestemme, om forskellene mellem hver testgruppe er signifikant sammenlignet med forskellene i hver testgruppe.
ANOVA 2-Way (ANOVA2way)
Beregner en uafhængig variansanalyse til at sammenligne middelværdierne for 2 til 20 populationer. En sammenfatning af resultaterne lagres i variablen stat.results.
ANOVA 2-Way-variansanalyse undersøger effekten af to uafhængige variabler og hjælper med at bestemme, om disse vekselvirker med den afhængige variabel. (Med andre ord, hvis de to uafhængige variabler vekselvirker, kan deres kombinerede effekt være større eller mindre end de enkelte uafhængige variablers effekter lagt sammen).
Testen anvendes til at beregne differenser ligesom ANOVA-analysen, men med yderligere en mulig indflydelse tilføjet. For at fortsætte med ANOVA kasseeksemplet kan ANOVA 2-Way muligvis undersøge kassematerialernes indflydelse på de fundne forskelle.
Valg af en alternativ hypotese (ƒ < >)
De fleste værktøjer til at udføre statistiske tests beder dog om at vælge en ud af tre alternative hypoteser.
| • | Den første er en ƒ alternativ hypotese, som f.eks mƒm0 til z -testen. |
| • | Den anden er en < alternativ hypotese, som f.eks. m1<m2 til t-test for to middelværdier. |
| • | Den tredje er en > alternativ hypotese, som f.eks. p1>p2 til z-test for to andele. |
Flyt markøren til det ønskede alternativ, og tryk på Enter for at vælge en alternativ hypotese.
Vælge indstillingen Samlet
Samlet (kun for t-test for to middelværdier og t-interval for to middelværdier) angiver, om varianserne skal kombineres til en samlet varians i beregningen.
| • | Vælg Nej, hvis du ikke vil have varianserne samlet. Populationsvarianser kan være forskellige. |
| • | Vælg Ja, hvis du vil have varianserne samlet. Populationsvarianser antages at være lig hinanden. |
Vælg Ja i rullemenuen for at vælge funktionen Samlet.