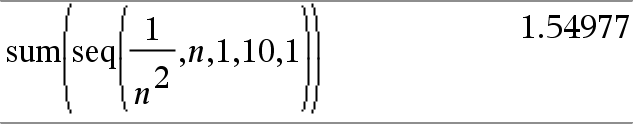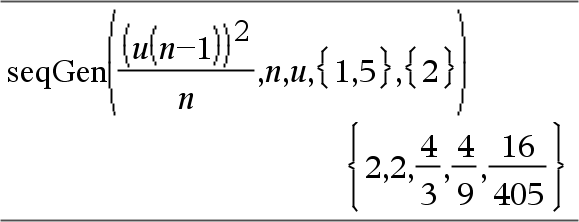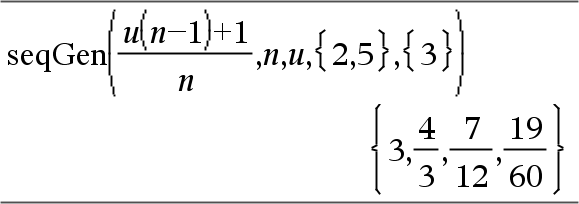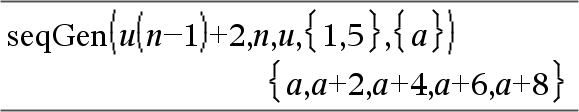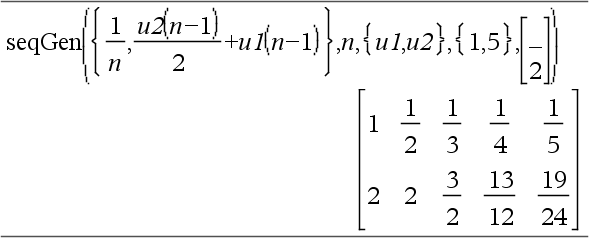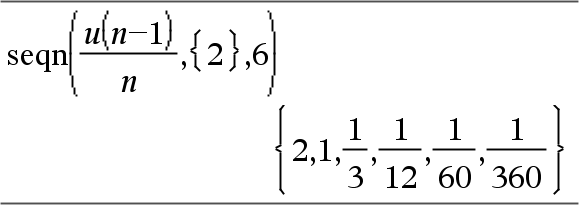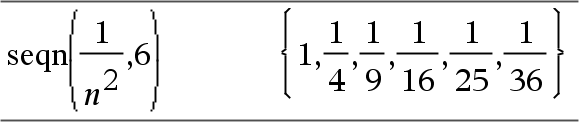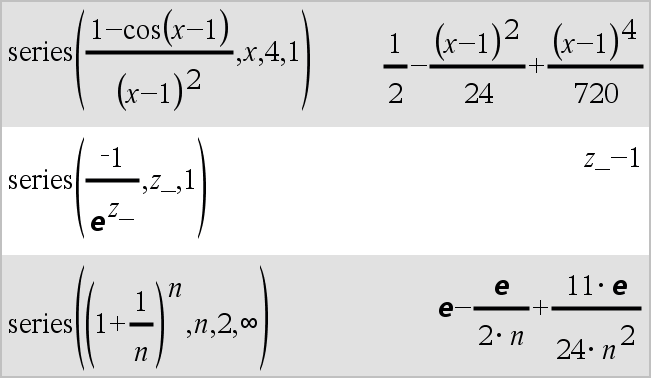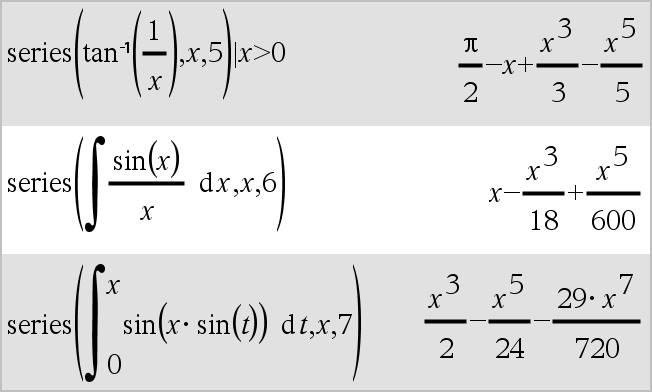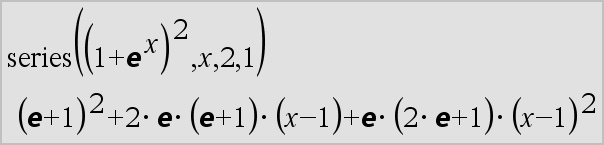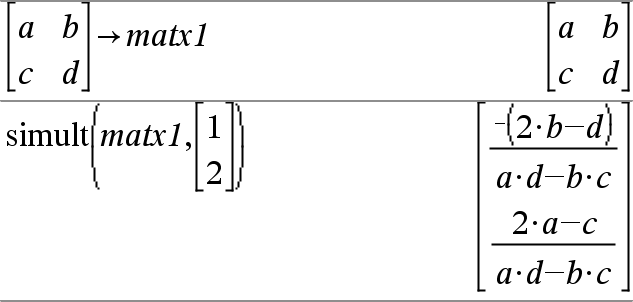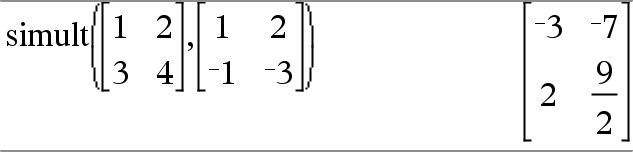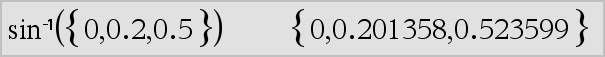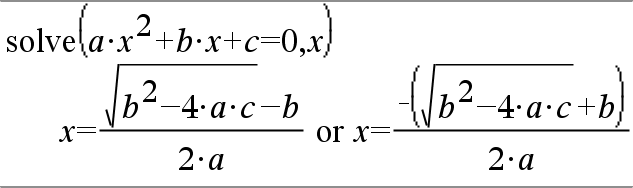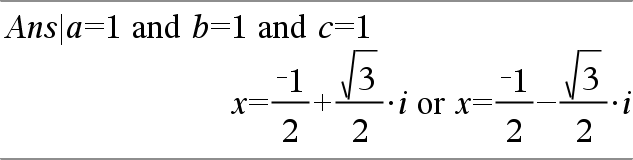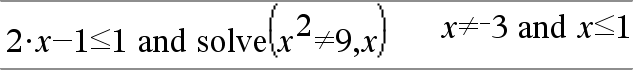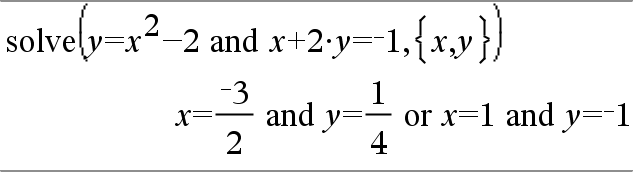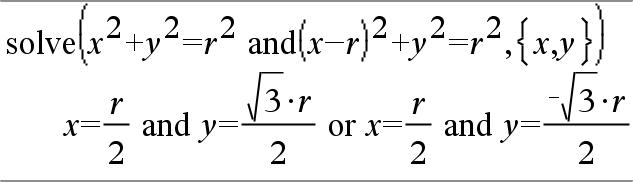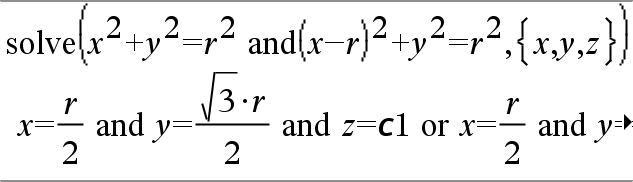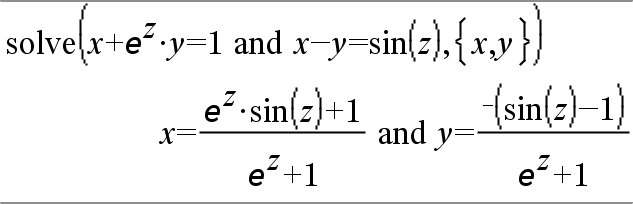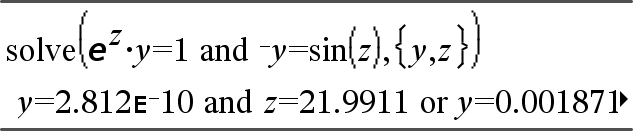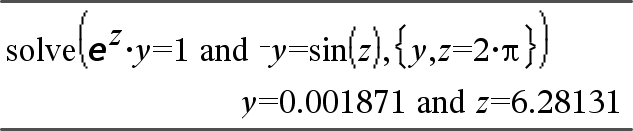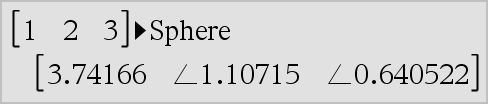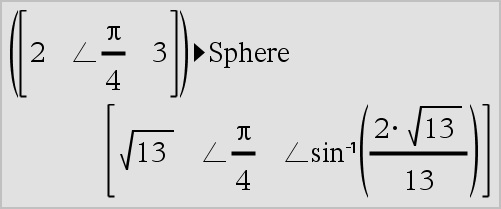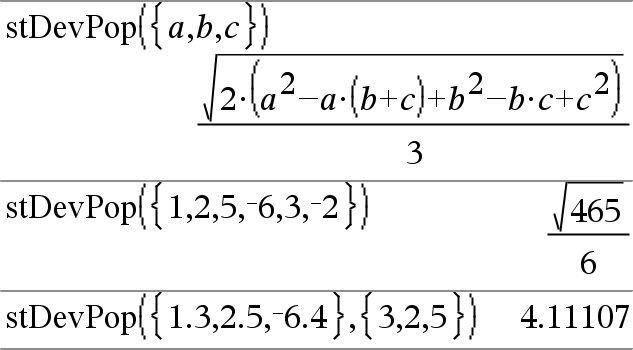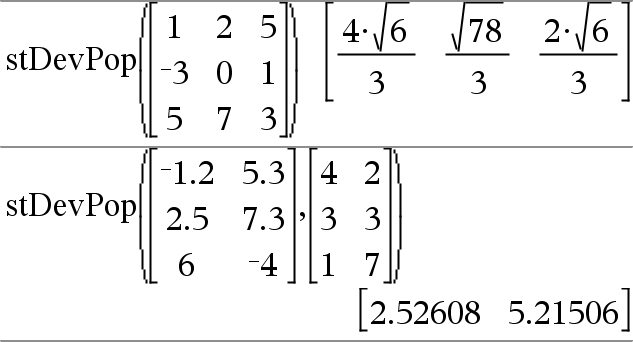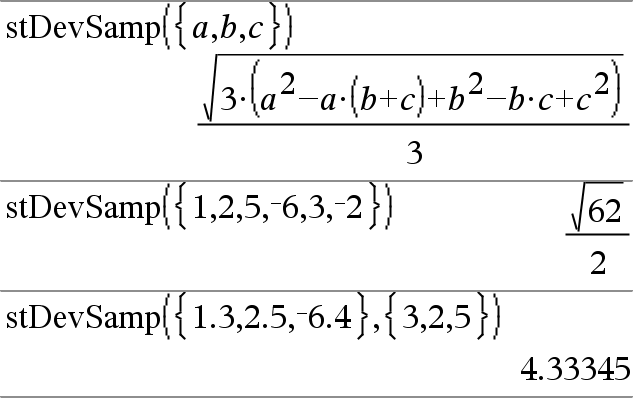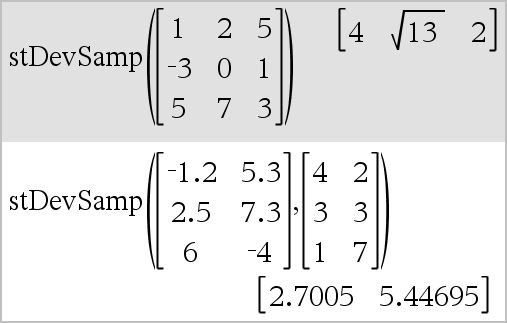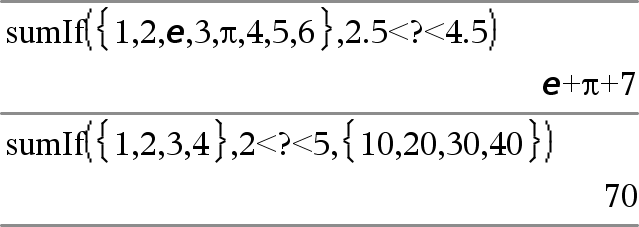|
µ tecla |
|
|
sec(Expr1) Þ expresión sec(Lista1) Þ lista Entrega la secante de Expr1 o entrega una lista que contiene las secantes de todos los elementos en Lista1. Nota: El argumento se interpreta como un ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual. Se puede usar ¡, G, o R para anular el modo de ángulo en forma temporal. |
En modo de ángulo en Grados:
|
|
µ tecla |
|
|
sec/(Expr1) Þ expresión sec/(Lista1) Þ lista Entrega el ángulo cuya secante es Expr1 o entrega una lista que contiene las secantes inversas de cada elemento de Lista1. Nota: El resultado se entrega como un ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual. Nota: Usted puede insertar esta función desde el teclado al escribir arcsec(...). |
En modo de ángulo en Grados:
En modo de ángulo en Gradianes:
En modo de ángulo en Radianes:
|
|
Catálogo > |
|
|
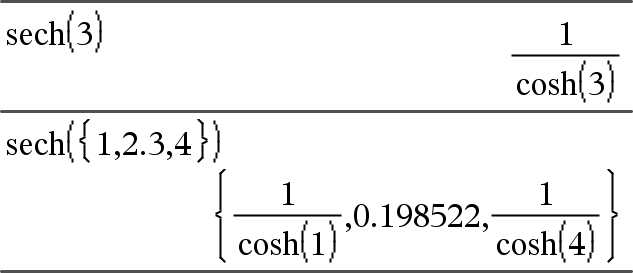
sech(Expr1) Þ expresión sech(Lista1) Þ lista Entrega la secante hiperbólica de Expr1 o entrega una lista que contiene las secantes hiperbólicas de los elementos de Lista1 . |
|
|
Catálogo > |
|
|
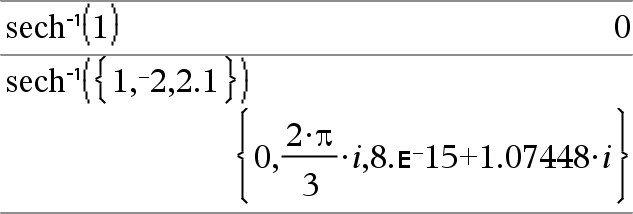
sech/(Expr1) Þ expresión sech/ (Lista1) Þ lista Entrega la secante hiperbólica inversa de Expr1 o entrega una lista que contiene las secantes hiperbólicas inversas de cada elemento de Lista1. Nota: Usted puede insertar esta función desde el teclado al escribir arcsech(...). |
En el modo de ángulo en Radianes y el modo complejo Rectangular:
|
|
Menú del Concentrador |
|
|
Comando de programación: Envía uno o más TI-Innovator™ Hub comandos a un concentrador conectado. exprOrString debe ser un comando válido TI-Innovator™ Hub . En general, exprOrString contiene un comando "SET ..." para controlar un dispositivo o un comando "READ ..." para solicitar datos. Los argumentos se envían al concentrador sucesivamente. Nota: Puede usar el comando Send dentro de un programa definido por el usuario pero no dentro de una función. Nota: Consulte además Get (aquí), GetStr (aquí) y eval() (aquí). |
Ejemplo: Encienda el elemento azul del LED RGB incorporado durante 0.5 segundos.
Ejemplo: Solicite el valor actual del sensor de nivel de luz incorporado del concentrador. Un comando Get recupera el valor y lo asigna a lightval variable.
Ejemplo: Envíe una frecuencia calculada a la bocina incorporada del concentrador. Use la variable especial iostr.SendAns para mostrar el comando del concentrador con la expresión evaluada.
|
|
Catálogo > |
|
|
seq(Expr, Var, Bajo, Alto[, Paso])Þlista Incrementa Var desde Bajo hasta Alto por un incremento de Paso, evalúa Expr y entrega los resultados como una lista. Los contenidos originales de Var están ahí todavía después de que se completa El valor predeterminado para Paso = 1.
|
Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
|
|
Catálogo > |
|
|
Genera una lista de términos para la secuencia varDep(Var)=Expr como sigue: Incrementa la variable independiente Var desde Var0 hasta VarMax por medio de PasoVar, evalúa varDep(Var) para los valores correspondientes de Var usando la fórmula Expr y ListaDeTérminosInic, y entrega los resultados como una lista.
Genera una matriz de términos para un sistema (o una lista) de secuencias ListaDeVarsDep(Var)=ListaOSistemaDeExpr como sigue: Incrementa la variable independiente Var desde Var0 hasta VarMax por medio de PasoVar, evalúa ListaDeVarsDep(Var) para los valores correspondientes de Var usando la fórmula ListaOSistemaDeExpr y MatrizDeTérminosInic, y entrega los resultados como una matriz. Los contenidos originales de Var no cambian después de que se completa El valor predeterminado para PasoVar = 1. |
Genera los 5 primeros términos de la secuencia u(n) = u(n-1)2/2, con u(1)=2 y PasoVar=1.
Ejemplo en el que Var0=2:
Sistema de dos secuencias:
Nota: El Vacío (_) en la matriz de términos iniciales anterior se usa para indicar que el término inicial para u1(n) se calcula utilizando la fórmula de secuencia explícita u1(n)=1/n. |
|
Catálogo > |
|
|
Genera una lista de términos para una secuencia u(n)=Expr(u, n) como sigue: Incrementa n desde 1 hasta nMax por 1, evalúa u(n) para los valores correspondientes de n usando la fórmula Expr(u, n) y ListaDeTérminosInic, y entrega los resultados como una lista.
Genera una lista de términos para una secuencia no recursiva u(n)=Expr(n) como sigue: Incrementa n desde 1 hasta nMax por 1, evalúa u(n) para los valores correspondientes de n usando la fórmula Expr(n) y entrega los resultados como una lista. Si nMax falta, nMax se configura a 2500 Si nMax=0, nMax se configura a 2500 Nota: |
Genera los 6 primeros términos de la secuencia u(n) = u(n-1)/2, con u(1)=2.
|
|
Catálogo > |
|
|
series(Expr1, Var, Orden [, Punto])Þexpresión series(Expr1, Var, Orden [, Punto]) | Var>PuntoÞexpresión series(Expr1, Var, Orden [, Punto]) | Var<PuntoÞexpresión
Entrega una representación de serie de potencia truncada de Expr1 expandida alrededor de Punto a través del grado Orden. Orden puede ser cualquier número racional. Las potencias resultantes de (Var N Punto) pueden incluir exponentes negativos y/o fraccionales. Los coeficientes de estas potencias pueden incluir logaritmos de (Var N Punto) y otras funciones de Var que están dominadas por todas las potencias de (Var N Punto) teniendo el mismo signo de exponente. Punto se predetermina a 0. Punto puede ser ˆ o Nˆ, en cuyos casos la expansión es por medio del grado Orden en 1/(Var N Punto). series(...) entrega “series(...)” si es incapaz de determinar tal representación, como para singularidades esenciales como sin(1/z) en z=0, eN1/z en z=0 ó ez en z = ˆ o Nˆ. Si la serie o una de sus derivadas tiene una discontinuidad de salto en Punto, es probable que el resultado contenga subexpresiones del signo de forma(…) o abs(…) para una variable de expansión real o (-1)piso(…angle(…)…) para una variable de expansión compleja, que es una que termina con “_”. Si usted intenta usar la serie sólo para los valores en un lado de Punto, entonces añada el apropiado de “| Var > Punto”, “| Var < Punto”, “| “Var | Punto” o “Var { Punto” para obtener un resultado más sencillo. series() puede proporcionar aproximaciones simbólicas para integrales indefinidas e integrales definidas para las cuales de otro modo no se pueden obtener soluciones simbólicas . series() se distribuye sobre listas y matrices del 1er argumento. series() es una versión generalizada de taylor(). Conforme se ilustra por medio del último ejemplo de la derecha, la corriente abajo de las rutinas de despliegue del resultado producido por serie(...) podría rearreglar los términos de manera que el término dominante no sea el del extremo izquierdo. Nota: Vea también dominantTerm(), aquí. |
|
|
Catálogo > |
|
|
setMode(enteroNombreModo, enteroConfig) Þentero setMode(lista) Þlista de enteros Sólo es válido dentro de una función o un programa. setMode(enteroNombreModo, enteroConfig) configura en forma temporal el modo enteroNombreModo a la nueva configuración enteroConfigy entrega un entero correspondiente a la configuración original de ese modo. El cambio está limitado a la duración de la ejecución del programa/la función. enteroNombreModo especifica cuál modo usted desea configurar. Debe ser uno de los enteros de modo de la tabla de abajo. enteroConfig especifica la nueva configuración para el modo. Debe ser uno de los enteros de configuración que se enumeran abajo para el modo específico que usted está configurando. setMode(lista) le permite cambiar varias configuraciones. lista contiene pares de enteros de modo y enteros de configuración. setMode(lista) entrega una lista similar cuyos pares de enteros representan los modos y las configuraciones originales. Si usted ha guardado todas las configuraciones de modo con getMode(0) & var, podrá usar setMode(var) para restaurar esas configuraciones hasta que la función o el programa exista. Vea getMode(), aquí. Nota: Las configuraciones del modo actual se pasan a las subrutinas llamadas. Si cualquier subrutina cambia una configuración del modo, el cambio de modo se perderá cuando el control regrese a la rutina de llamada. Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto. |
Despliegue el valor aproximado de p usando la configuración predeterminada para Desplegar Dígitos, y luego despliegue p con una configuración de Fijo2. Revise para ver que el predeterminado esté restaurado después de que se ejecute el programa.
|
|
Modo Nombre |
Modo Entero |
Cómo configurar enteros |
|
Desplegar dígitos |
1 |
1=Flotante, 2=Flotante1, 3=Flotante2, 4=Flotante3, 5=Flotante4, 6=Flotante5, 7=Flotante6, 8=Flotante7, 9=Flotante8, 10=Flotante9, 11=Flotante10, 12=Flotante11, 13=Flotante12, 14=Fijo0, 15=Fijo1, 16=Fijo2, 17=Fijo3, 18=Fijo4, 19=Fijo5, 20=Fijo6, 21=Fijo7, 22=Fijo8, 23=Fijo9, 24=Fijo10, 25=Fijo11, 26=Fijo12 |
|
Ángulo |
2 |
1=Radián, 2=Grado, 3=Gradián |
|
Formato exponencial |
3 |
1=Normal, 2=Científico, 3=Ingeniería |
|
Real o Complejo |
4 |
1=Real, 2=Rectangular, 3=Polar |
|
Auto o Aprox. |
5 |
1=Auto, 2=Aproximado |
|
Formato de Vector |
6 |
1=Rectangular, 2=Cilíndrico, 3=Esférico |
|
Base |
7 |
1=Decimal, 2=Hexagonal, 3=Binario |
|
Sistema de unidad |
8 |
1=SI, 2=Ing/EEUU |
|
Catálogo > |
|
|
shift(Entero1[,#deCambios])Þentero Cambia los bits en un entero binario. Usted puede ingresar Entero1 en cualquier base de números; se convierte automáticamente en una forma binaria de 64 bits signada. Si la magnitud de Entero1 es demasiado grande para esta forma, una operación de módulo simétrico lo lleva dentro del rango. Para obtener más información, vea 4Base2, aquí. Si #deCambios es positivo, el cambio es hacia la izquierda. Si #deCambios es negativo, el cambio es hacia la derecha. El predeterminado es L1 (cambiar a la derecha un bit). En un cambio a la derecha, el bit del extremo derecho se elimina y 0 ó 1 se inserta para coincidir con el bit del extremo izquierdo. En un cambio a la izquierda, el bit del extremo izquierdo se elimina y 0 ó 1 se inserta como el bit del extremo derecho. Por ejemplo, en un cambio a la derecha: Cada bit cambia a la derecha. 0b0000000000000111101011000011010 Inserta 0 si el bit del extremo izquierdo es 0, ó 1 si el bit del extremo izquierdo es 1. produce: 0b00000000000000111101011000011010 El resultado se despliega de acuerdo con el modo de la Base. Los ceros líderes no se muestran. |
En modo de base binaria:
En modo de base hexadecimal:
Importante: Para ingresar un número binario o hexadecimal, use siempre el prefijo 0b ó 0h (cero, no la letra O). |
|
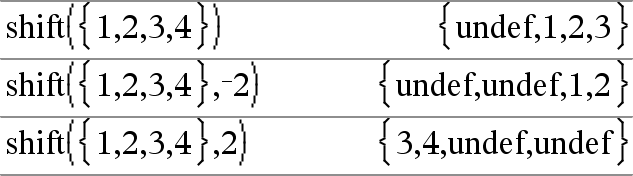
shift(Lista1 [,#deCambios])Þlista Entrega una copia de Lista1 cambiada a la derecha o a la izquierda por elementos de #de Cambios . No altera Lista1. Si #deCambios es positivo, el cambio es hacia la izquierda. Si #deCambios es negativo, el cambio es hacia la derecha. El predeterminado es L1 (cambiar a la derecha un elemento). Los elementos introducidos al principio o al final de lista por medio del cambio están configurados al símbolo “indef”. |
En modo de base decimal:
|
|
shift(Cadena1 [,#deCambios])Þcadena Entrega una copia de Cadena1 cambiada a la derecha o a la izquierda por caracteres de #de Cambios . No altera Cadena1. Si #deCambios es positivo, el cambio es hacia la izquierda. Si #deCambios es negativo, el cambio es hacia la derecha. El predeterminado es L1 (cambiar a la derecha un caracter). Los caracteres introducidos al principio o al final de cadena por medio del cambio están configurados a un espacio. |
|
|
Catálogo > |
|
|
sign(Expr1)Þexpresión sign(Lista1)Þlista sign(Matriz1)Þmatriz Para Expr1real o compleja, entrega Expr1/abs(Expr1) cuando Expr1ƒ 0. Entrega 1 si Expr1 es positiva. Entrega L1 si Expr1 es negativa. sign(0) entrega „1 si el modo de formato complejo es Real; de otro modo, se entrega a sí mismo. sign(0) representa el círculo de unidad en el dominio complejo. Para una lista o matriz, entrega los signos de todos los elementos. |
Si el modo de formato complejo es Real:
|
|
Catálogo > |
|||||||
|
simult(matrizCoef, vectorConst[, Tol])Þmatriz Entrega un vector de columna que contiene las soluciones para un sistema de ecuaciones lineales. Nota: Vea también matrizCoef debe ser una matriz cuadrada que contiene los coeficientes de las ecuaciones. vectorConst debe tener el mismo número de filas (misma dimensión) que matrizCoef y contener las constantes. De manera opcional, cualquier elemento de matriz se trata como cero si su valor absoluto es menor que la Tolerancia. Esta tolerancia se usa sólo si la matriz tiene ingresos de punto flotante y no contiene ninguna variable simbólica a la que no se le haya asignado un valor. De otro modo, la Tolerancia se ignora.
|
Solucione para x y y: x + 2y = 1 3x + 4y = L1
La solución es x=L3 y y=2.
Solución: ax + by = 1 cx + dy = 2
|
||||||
|
simult(matrizCoef, matrizConst[, Tol])Þmatriz Soluciona varios sistemas de ecuaciones lineales, donde cada sistema tiene los mismos coeficientes de ecuaciones pero constantes diferentes. Cada columna en matrizConst debe contener las constantes para un sistema de ecuaciones. Cada columna en la matriz resultante contiene la solución para el sistema correspondiente. |
Solucionar: x + 2y = 1 3x + 4y = L1
x + 2y = 2 3x + 4y = L3
Para el primer sistema, x=L3 y y=2. Para el segundo sistema, x=L7 y y=9/2. |
|
Catálogo > |
|
|
Expr 4sin Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @>sin. Representa Expr en términos de seno. Este es un operador de conversión de despliegue. Se puede usar únicamente al final de la línea de ingreso. 4sin reduce todas las potencias de cos(...) módulo 1Nsen(...)^2 e manera que cualquier potencia restante de sen(...) tiene exponentes en el rango (0, 2). Entonces, el resultado estará libre de cos(...) si y sólo si cos(...) ocurre en la expresión dada únicamente para potencias iguales. Nota: Este operador de conversión no está soportado en los modos de Ángulo en Grados o Gradianes. Antes de usarlo, asegúrese de que el modo de Ángulo está configurado a Radianes y que Expr no contiene referencias explícitas para ángulos en grados o gradianes. |
|
|
µ tecla |
|
|
sin(Expr1)Þexpresión sin(Lista1)Þlista
sin(Lista1) entrega una lista de senos de todos los elementos en Lista1. Nota: El argumento se interpreta como un ángulo en grados, gradianes o radianes, de acuerdo con el modo del ángulo actual. Usted puede usar ¡,G o R para anular la configuración del modo de ángulo en forma temporal. |
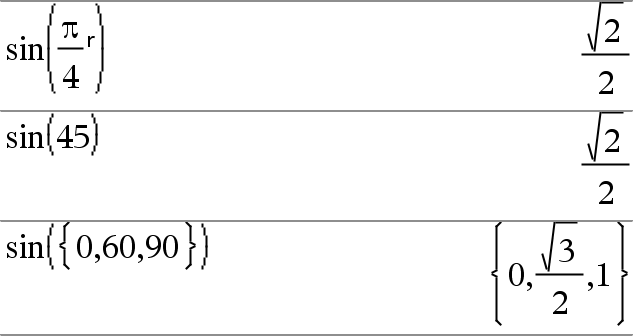
En modo de ángulo en Grados:
En modo de ángulo en Gradianes:
En modo de ángulo en Radianes:
|
|
sin(matrizCuadrada1)ÞmatrizCuadrada Entrega el seno de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el seno de cada elemento. Para obtener información acerca del método de cálculo, consulte cos(). matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante. |
En modo de ángulo en Radianes:
|
|
µ tecla |
|
|
sin/(Expr1)Þexpresión sin/(Lista1)Þlista
sin/(Lista1) entrega una lista de senos inversos de cada elemento de Lista1. Nota: El resultado se entrega como un ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual. Nota: Usted puede insertar esta función desde el teclado al escribir arcosen(...). |
En modo de ángulo en Grados:
En modo de ángulo en Gradianes:
En modo de ángulo en Radianes:
|
|
sin/(matrizCuadrada1)ÞmatrizCuadrada Entrega el seno inverso de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el seno inverso de cada elemento. Para obtener información acerca del método de cálculo, consulte cos(). matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante. |
En el modo de ángulo en Radianes y el modo de formato complejo Rectangular:
|
|
Catálogo > |
|
|
sinh(Expr1)Þexpresión sinh(Lista1)Þlista
sinh (Lista1) entrega una lista de los senos hiperbólicos de cada elemento de Lista1. |
|
|
sinh(matrizCuadrada1)ÞmatrizCuadrada Entrega el seno hiperbólico de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el seno hiperbólico de cada elemento. Para obtener información acerca del método de cálculo, consulte cos(). matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante. |
En modo de ángulo en Radianes:
|
|
Catálogo > |
|
|
sinh/(Expr1)Þexpresión sinh/(Lista1)Þlista
sinh/(Lista1) entrega una lista de los senos hiperbólicos inversos de cada elemento de Lista1. Nota: Usted puede insertar esta función desde el teclado al escribir arcosenh(...). |
|
|
sinh/(matrizCuadrada1)ÞmatrizCuadrada Entrega el seno hiperbólico inverso de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el seno hiperbólico inverso de cada elemento. Para obtener información acerca del método de cálculo, consulte cos(). matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante. |
En modo de ángulo en Radianes:
|
|
Catálogo > |
|
|
SinReg X, Y [ , [Iteraciones] ,[ Periodo] [, Categoría, Incluir] ] Resuelve la regresión sinusoidal en las listas X y Y. Se almacena un resumen de resultados en la variable stat.results (aquí). Todas las listas deben tener una dimensión igual, excepto por Incluir. X y Y son listas de variables independientes y dependientes. Iteraciones es un valor que especifica el número máximo de veces (1 a 16) que se intentará una solución. Si se omite, se usa 8. Por lo general, los valores más grandes dan como resultado una mejor exactitud, pero tiempos de ejecución más largos, y viceversa. Periodo especifica un periodo estimado. Si se omite, la diferencia entre los valores en X deberán ser iguales y estar en orden secuencial. Si usted especifica el Periodo, las diferencias entre los valores x pueden ser desiguales. Categoría es una lista de códigos de categoría para los datos X y Y correspondientes. Incluir es una lista de uno o más códigos de categoría. Sólo aquellos elementos de datos cuyo código de categoría está incluido en esta lista están incluidos en el cálculo. El resultado de SinReg siempre es en radianes, independientemente de la configuración del modo de ángulo. Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (aquí). |
|
|
Variable de salida |
Descripción |
|
stat.EcnReg |
Ecuación de Regresión: a·sen(bx+c)+d |
|
stat.a, stat.b, stat.c, stat.d |
Coeficientes de regresión |
|
stat.Resid |
Residuales de la regresión |
|
stat.XReg |
La lista de puntos de datos en la Lista X modificada que se usa en realidad en la regresión con base en las restricciones de las Categorías Frec, Lista de Categoríae Incluir |
|
stat.YReg |
La lista de puntos de datos en la Lista Y modificada que se usa en realidad en la regresión con base en las restricciones de las Categorías Frec, Lista de Categoríae Incluir |
|
stat.FrecReg |
Lista de frecuencias correspondientes a stat.XReg y stat.YReg |
|
Catálogo > |
|
|
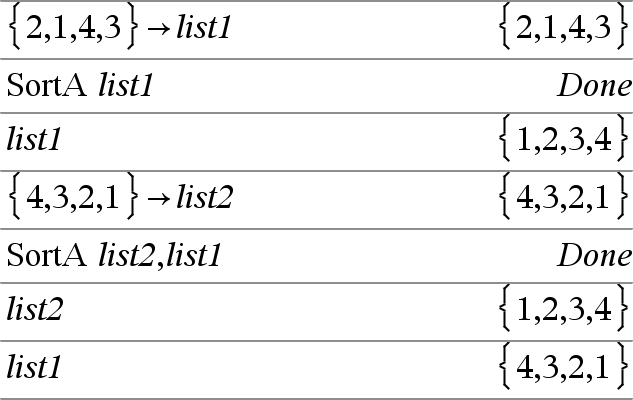
SortA Lista1[, Lista2] [, Lista3] ... SortA Vector1[, Vector2] [, Vector3] ... Ordena los elementos del primer argumento en orden ascendente. Si usted incluye argumentos adicionales, ordena los elementos de cada uno, de manera que sus nuevas posiciones coinciden con las nuevas posiciones de los elementos en el primer argumento. Todos los argumentos deben ser nombres de listas o vectores. Todos los argumentos deben tener dimensiones iguales. Los elementos vacíos (inválidos) dentro del primer argumento se mueven a la parte inferior. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
Catálogo > |
|
|
SortD Lista1[, Lista2] [, Lista3] ... SortD Vector1[,Vector2] [,Vector3] ... Idéntico a SortA, excepto que SortD ordena los elementos en orden descendente. Los elementos vacíos (inválidos) dentro del primer argumento se mueven a la parte inferior. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
Catálogo > |
|
|
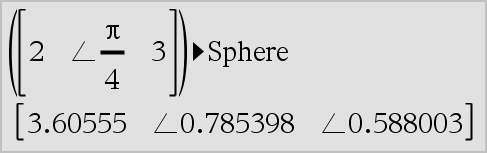
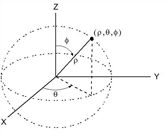
Vector 4Sphere Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @>Sphere. Despliega el vector de fila o columna en forma esférica [r ±q ±f]. Vector debe ser de dimensión 3 y puede ser un vector de fila o de columna. Nota: 4Sphere es una instrucción de formato de despliegue, no una función de conversión. Usted puede usarla sólo al final de una línea de ingreso. |
Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
Presione ·
|
|
Catálogo > |
|
|
sqrt(Expr1)Þexpresión sqrt(Lista1)Þlista Entrega la raíz cuadrada del argumento. Para una lista, entrega las raíces cuadradas de todos los elementos en Lista1. Nota: Vea también Plantilla de raíz cuadrada, aquí. |
|
|
Catálogo > |
|
|
stat.results Despliega los resultados de un cálculo de estadísticas. Los resultados se despliegan como un conjunto de pares de valores de nombres Los nombres específicos que se muestran dependen de la función o del comando de estadísticas evaluado de manera más reciente. Usted puede copiar un nombre o valor y pegarlo en otras ubicaciones.
Nota: Evite definir variables que usan los mismos nombres que aquellos que se usan para análisis estadístico. En algunos casos, podría ocurrir una condición de error. Los nombres de variable que se usan para análisis estadístico se enumeran en la tabla de abajo. |
|
|
stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d |
stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX |
stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y |
stat.Q3X stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx stat.sy stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS |
stat.SSBlock stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1 stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w stat.y stat.yList stat.YReg |
|
Nota: Cada vez que la aplicación de Listas y Hoja de Cálculo calcula resultados estadísticos, copia las variables del grupo “stat.” a un grupo “stat#.”, donde # es un número que se incrementa en forma automática. Esto le permite mantener los resultados anteriores mientras realiza varios cálculos. |
|
Catálogo > |
|
|
stat.values Despliega una matriz de los valores calculados para la función o el comando de estadísticas evaluado de manera más reciente. A diferencia de stat.results, stat.values omite los nombres asociados con los valores. Usted puede copiar un valor y pegarlo en otras ubicaciones. |
Vea el ejemplo de stat.results. |
|
Catálogo > |
|
|
stDevPop(Lista[, listaFrec])Þexpresión Entrega la desviación estándar de población de los elementos en Lista. Cada elemento de listaFrec cuenta el número de ocurrencias consecutivas del elemento correspondiente en Lista. Nota: Lista debe tener al menos dos elementos. Los elementos vacíos (inválidos) se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. |
En modos de ángulo en Radianes y auto:
|
|
stDevPop(Matriz1[, matrizFrec])Þmatriz Entrega un vector de fila de las desviaciones estándar de población las columnas en Matriz1. Cada elemento de matrizFrec cuenta el número de ocurrencias consecutivas del elemento correspondiente en Matriz1. Nota: Matriz1 debe tener al menos dos filas. Los elementos vacíos (inválidos) se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
Catálogo > |
|
|
stDevSamp(Lista[, listaFrec])Þexpresión Entrega la desviación estándar muestra de los elementos en Lista. Cada elemento de listaFrec cuenta el número de ocurrencias consecutivas del elemento correspondiente en Lista. Nota: Lista debe tener al menos dos elementos. Los elementos vacíos (inválidos) se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
stDevSamp(Matriz1[, matrizFrec])Þmatriz Entrega un vector de fila de las desviaciones estándar muestra de las columnas en Matriz1. Cada elemento de matrizFrec cuenta el número de ocurrencias consecutivas del elemento correspondiente en Matriz1. Nota: Matriz1 debe tener al menos dos filas. Los elementos vacíos (inválidos) se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
Catálogo > |
|
|
Stop Comando de programación: Termina el programa. Stop no está permitido en las funciones. Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto. |
|
|
Vea & (almacenar), aquí. |
|
|
|
|
|
Catálogo > |
|
|
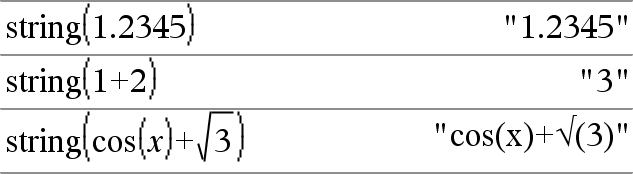
string(Expr)Þcadena Simplifica Expr y entrega el resultado de una cadena de caracteres. |
|
|
Catálogo > |
|
|
subMat(Matriz1[, iniciarFila] [, iniciarCol] [, terminarFila] [, terminarCol]) Þmatriz Entrega la submatriz especificada de Matriz1. Predeterminados: iniciarFila=1, iniciarCol=1, terminarFila=última fila, terminarCol=última columna. |
|
|
Vea G(), aquí. |
|
|
|
|
|
Catálogo > |
|
|
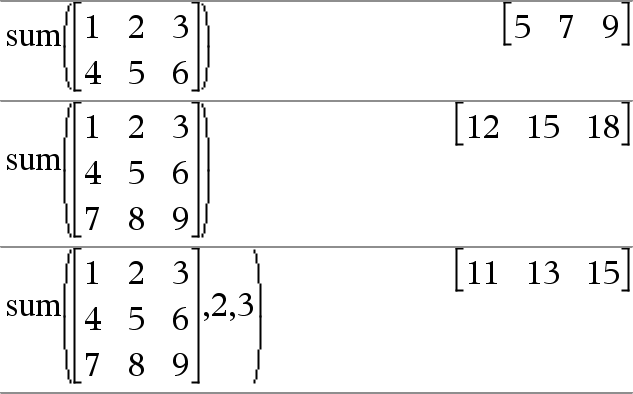
sum(Lista[, Iniciar[, Terminar]])Þexpresión Entrega la suma de todos los elementos en Lista. Inicio y Término son opcionales. Especifican un rango de elementos. Cualquier argumento inválido produce un resultado inválido. Los elementos vacíos (inválidos) en Lista se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
sum(Matriz1[, Iniciar[, Terminar]])Þmatriz Entrega un vector de fila que contiene las sumas de todos los elementos en las columnas de Matriz1. Inicio y Término son opcionales. Especifican un rango de filas. Cualquier argumento inválido produce un resultado inválido. Los elementos vacíos (inválidos) en Matriz1 se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. |
|
|
Catálogo > |
|||||||
|
sumIf(Lista,Criterios[, ListaSuma])Þvalor Entrega la suma acumulada de todos los elementos en Lista que cumplen con los Criteriosespecificados. De manera opcional, usted puede especificar una lista alterna, listaSuma, para proporcionar los elementos a acumular. Lista puede ser una expresión, lista o matriz. ListaSuma, si se especifica, debe tener la(s) misma(s) dimensión(es) que Lista. Los criterios pueden ser:
Cuando un elemento de Lista cumple con los Criterios, el elemento se agrega a la suma acumulativa. Si usted incluye listaSuma, el elemento correspondiente de listaSuma se agrega a la suma en su lugar. Dentro de la aplicación de Listas y Hoja de Cálculo, usted puede usar un rango de celdas en lugar de Lista y listaSuma. Los elementos vacíos (inválidos) se ignoran. Para obtener más información sobre elementos vacíos, vea aquí. Nota: Vea también countIf(), aquí. |
|
|
Vea G(), aquí. |
|
|
|
|
|
Catálogo > |
|
|
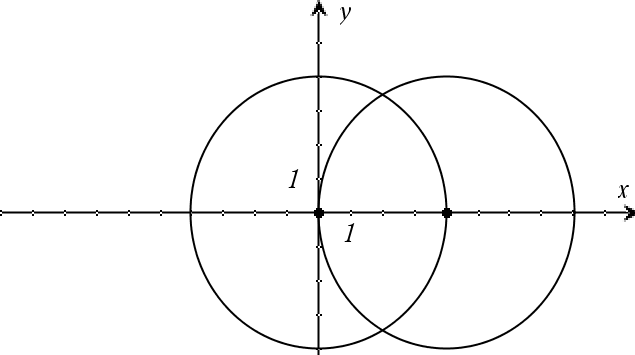
system(Ecn1 [, Ecn2 [, Ecn3 [, ...]]]) system(Expr1 [, Expr2 [, Expr3 [, ...]]]) Entrega un sistema de ecuaciones, formateado como una lista. Usted también puede crear un sistema al usar una plantilla.
|
|
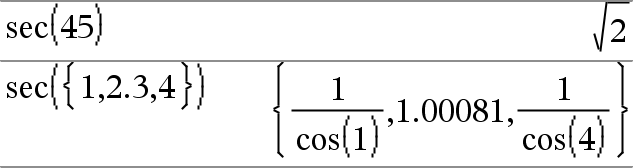







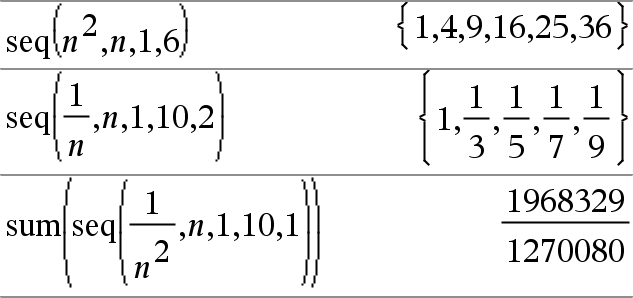
 .
.