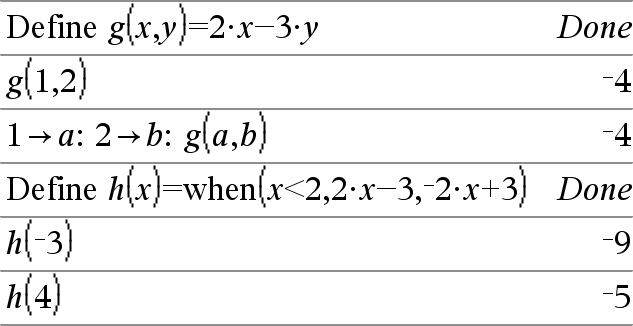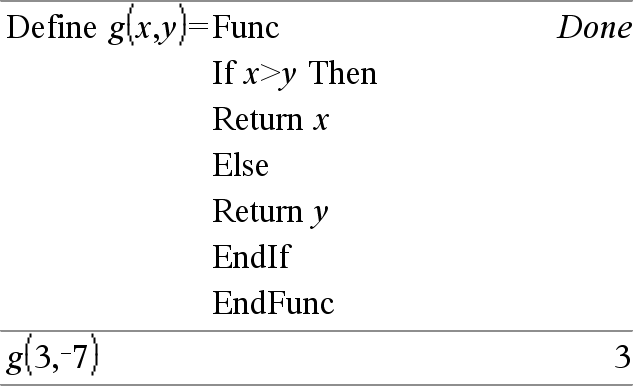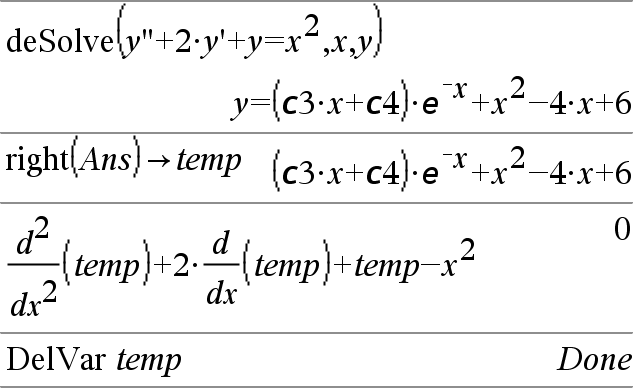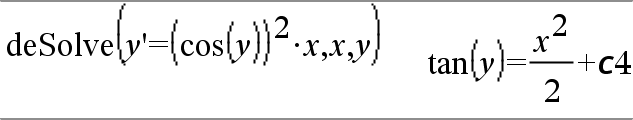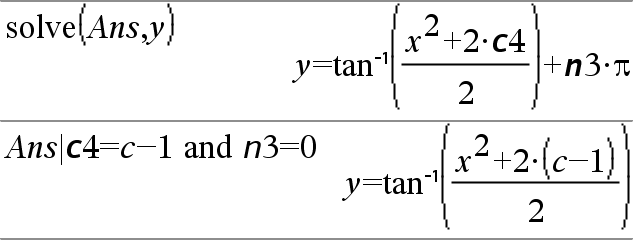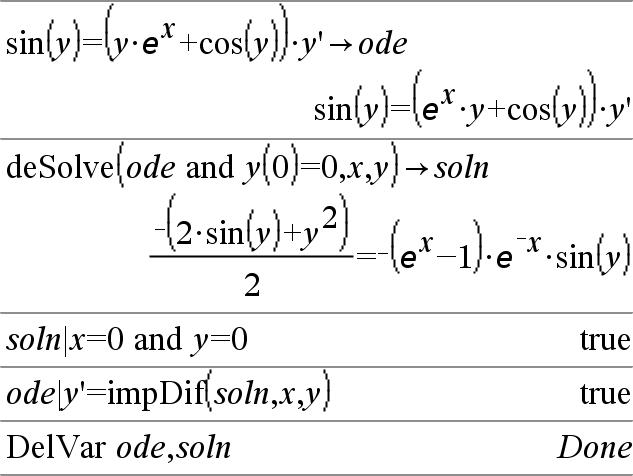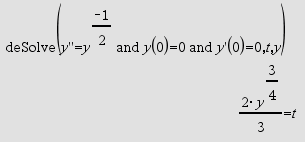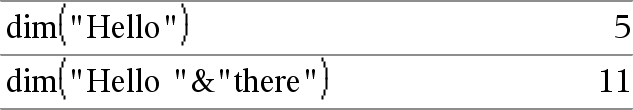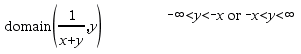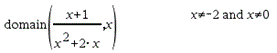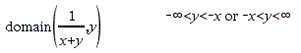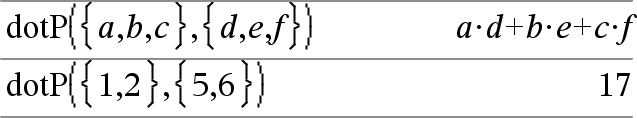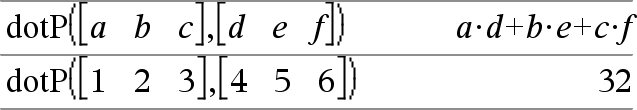D

dbd()

Catálogo >

dbd(fecha1,fecha2)Þvalor

Entrega el número de días entre fecha1 y fecha2 usando el método de conteo de días reales.

fecha1 y fecha2 pueden ser números dentro del rango de las fechas en el calendario estándar. Si tanto fecha1 como fecha2 son listas, deberán tener la misma longitud.

Tanto fecha1 como fecha2 deben estar entre los años 1950 a 2049.

Usted puede ingresar las fechas en uno de dos formatos. La colocación decimal se diferencia entre los formatos de fecha.

MM.DDAA (formato que se usa de manera común en los Estados Unidos) DDMM.AA (formato que se usa de manera común en Europa)

4DD

Catálogo >

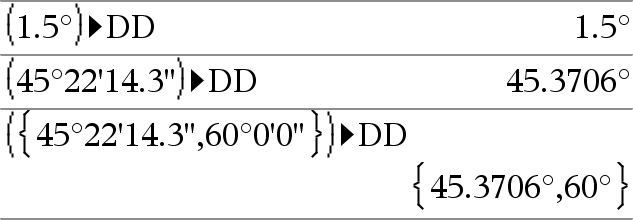
Expr1 4DDÞvalor

Lista1 4DDÞlista

Matriz1 4DDÞmatriz

Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @>DD.

Entrega el decimal equivalente del argumento expresado en grados. El argumento es un número, lista o matriz que se interpreta por medio de la configuración del modo de Ángulo en gradianes, radianes o grados.

En modo de ángulo en Grados:

 

En modo de ángulo en Gradianes:

 

En modo de ángulo en Radianes:

4Decimal

Catálogo >

Expresión1 4DecimalÞexpresión

Lista1 4DecimalÞexpresión

Matriz1 4DecimalÞexpresión

Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @>Decimal.

Despliega el argumento en forma decimal. Este operador se puede usar únicamente al final de la línea de ingreso.

Define (Definir)

Catálogo >

Define Var = Expresión

Define Función(Param1, Param2, ...) = Expresión

Define la variable Var o la función definida por el usuario Función.

Los parámetros, como Param1, proporcionan marcadores de posición para pasar argumentos a la función. Cuando llame a una función definida por el usuario, usted deberá suministrar argumentos (por ejemplo, valores o variables) que correspondan a los parámetros. Cuando se llama, la función evalúa la Expresión usando los argumentos provistos.

Var y Función no pueden ser el nombre de una variable de sistema o de una función o un comando integrado.

Nota: Esta forma de Define es equivalente a ejecutar la expresión: expresión & Función(Param1,Param2).

 

Define Función(Param1, Param2, ...) = Func
Bloque
EndFunc

Define Programa(Param1, Param2, ...) = Prgm
Bloque
EndPrgm

En esta forma, la función o el programa definido por el usuario puede ejecutar un bloque de varias sentencias.

Bloque puede ser una sentencia sencilla o una serie de sentencias en líneas separadas. Bloque también puede incluir expresiones e instrucciones (como If, Then, Else, y For).

Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Nota: Vea también Define LibPriv, aquíy Define LibPub, aquí.

 

Define LibPriv

Catálogo >

Define LibPriv Var = Expresión

Define LibPriv Función(Param1, Param2, ...) = Expresión

Define LibPriv Función(Param1, Param2, ...) = Func
Bloque
EndFunc

Define LibPriv Programa(Param1, Param2, ...) = Prgm
Bloque
EndPrgm

Opera igual que Define, excepto porque define una variable de librería privada, función o programa. Las funciones y los programas privados no aparecen en el Catálogo.

Nota: Vea también Define, aquí y Define LibPub, aquí.

 

Define LibPub

Catálogo >

Define LibPub Var = Expresión

Define LibPub Función(Param1, Param2, ...) = Expresión

Define LibPub Función(Param1, Param2, ...) = Func
Bloque
EndFunc

Define LibPub Programa(Param1, Param2, ...) = Prgm
Bloque
EndPrgm

Opera igual que Define, excepto porque define una variable de librería pública, función o programa. Las funciones y los programas públicos aparecen en el Catálogo después de que la librería se ha guardado y actualizado.

Nota: Vea también Define, aquí y Define LibPriv, aquí.

 

deltaList()

Vea @List(), aquí.

 

 

deltaTmpCnv()

Vea @tmpCnv(), aquí.

 

 

DelVar

Catálogo >

DelVar Var1[, Var2] [, Var3] ...

DelVar Var.

Borra la variable o el grupo de variables especificado de la memoria.

Si una o más de las variables están bloqueadas, este comando despliega un mensaje de error y borra únicamente las variables no bloqueadas. Vea unLock, aquí.

DelVar Var. borra todos los miembros del grupo de variables Var. (como las estadísticas stat.nn los resultados o las variables que se crean con el uso de LibShortcut() función). El punto (.) en esta forma de comando DelVar lo limita a borrar un grupo de variables; la variable sencilla Var no se ve afectada.

delVoid() (borrInválido)

Catálogo >

delVoid(Lista1)Þlista

Entrega una lista que tiene el contenido de Lista1 con todos los elementos (nulos) vacíos eliminados.

Para obtener más información sobre elementos vacíos, vea aquí.

derivative()

Vea d(), aquí.

 

 

deSolve() (resolverEd)

Catálogo >

deSolve(EDO1erO2oGrado, Var, depVar)Þuna solución general

Entrega una ecuación que especifica en forma explícita o implícita una solución general para la ecuación diferencial ordinaria (EDO) de 1er o 2o grado. En la EDO:

• Use un símbolo primo (presione º) para denotar la 1a derivada de la variable dependiente con respecto de la variable independiente.
• Use dos símbolos primos para denotar la segunda derivada correspondiente.

El símbolo primo se usa para las derivadas dentro de resolverEd() únicamente. En otros casos, use d().

La solución general de una ecuación de 1er grado contiene una constante arbitraria de la forma ck, donde k es un sufijo de entero desde 1 hasta 255. La solución de una ecuación de 2o grado contiene dos constantes.

Aplique solve() para una solución implícita si desea tratar de convertirla en una o más soluciones explícitas equivalentes.

Cuando compare sus resultados con las soluciones del libro de texto o del manual, tome en cuenta que los diferentes métodos introducen constantes arbitrarias en distintos puntos en el cálculo, lo que puede producir soluciones generales diferentes.

deSolve(EDO1erGradoandcondInic, Var, depVar) Þuna solución particular

Entrega una solución particular que satisface la EDO1erGrado y la condInic. Por lo general esto es más fácil que determinar una solución general, al sustituir los valores iniciales, solucionar la constante arbitraria y luego sustituir ese valor en la solución general.

condInic es una ecuación de la forma:

depVar (valorInicialIndependiente) = valorInicialDependiente

El valorIinicialIndependiente y el valorInicialDependiente pueden ser variables como x0 y y0 que no tienen ningún valor almacenado. La diferenciación implícita puede ayudar a verificar las soluciones implícitas.

deSolve(EDO2oGradoandcondIinic1andcondInic2, Var, depVar)Þuna solución particular

Entrega una solución particular que satisface la EDO de 2o Grado y tiene un valor especificado de la variable dependiente y su primera derivada en un punto.

Para condInic1, use la forma:

depVar (valorInicialIndependiente) = valorInicialDependiente

Para condIinic2, use la forma:

depVar (valorInicialIndependiente) = valorInicial1aDerivada

deSolve(EDO2oGradoandbndCond1andcondBnd2, Var, depVar)Þuna solución particular

Entrega una solución particular que satisface la EDO2oGrado y tiene valores especificados en dos puntos diferentes.

det()

Catálogo >

det(matrizCuadrada[, Tolerancia])Þexpresión

Entrega la determinante de matrizCuadrada.

De manera opcional, cualquier elemento de matriz se trata como cero si su valor absoluto es menor que la Tolerancia. Esta tolerancia se usa sólo si la matriz tiene ingresos de punto flotante y no contiene ninguna variable simbólica a la que no se le haya asignado un valor. De otro modo, la Tolerancia se ignora.

• Si usted usa /· o configura el modo Auto o Aproximado para aproximar, los cálculos se realizan al usar la aritmética de punto flotante.
• Si la Tolerancia se omite o no se usa, la tolerancia predeterminada se calcula como:

5EM14 ·max(dim(matrizCuadrada))·rowNorm(matrizCuadrada)

diag()

Catálogo >

diag(Lista)Þmatriz

diag(matrizFila)Þmatriz

diag(matrizColumna)Þmatriz

Entrega una matriz con los valores en la lista o matriz de argumentos en su diagonal principal.

diag(matrizCuadrada)ÞmatrizFila

Entrega una matriz de filas que contiene los elementos de la diagonal principal de matrizCuadrada.

matrizCuadrada debe ser cuadrada.

dim()

Catálogo >

dim(Lista)Þentero

Entrega la dimensión de Lista.

dim(Matriz)Þlista

Entrega las dimensiones de la matriz como una lista de dos elementos {filas, columnas}.

dim(Cadena)Þentero

Entrega el número de caracteres contenidos en la cadena de caracteres Cadena.

Disp

Catálogo >

Disp exprOCadena1 [, exprOCadena2] ...

Despliega los argumentos en el historial de la Calculadora . Los argumentos se despliegan en sucesión, con espacios pequeños como separadores.

Es útil principalmente con programas y funciones para asegurar en despliegue de cálculos intermedios.

Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

DispAt

Catálogo >

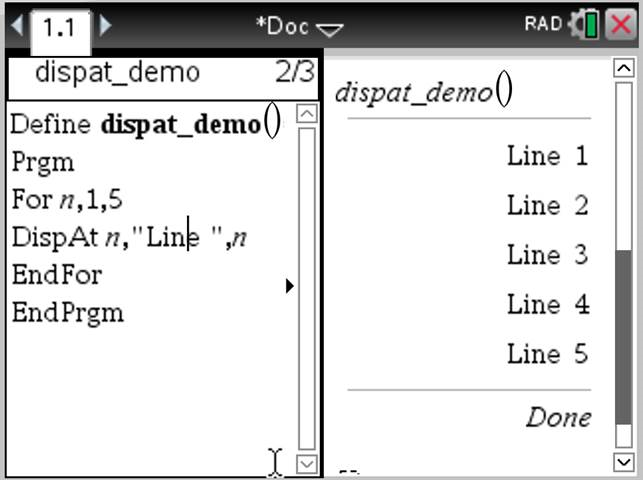
DispAt int,expr1 [,expr2 ...] ...

DispAt permite especificar la línea en la que se mostrará en la pantalla la expresión o cadena de caracteres especificada.

El número de línea se puede especificar como una expresión.

Tenga en cuenta que el número de línea no es para toda la pantalla, sino para el área inmediatamente después del comando/programa.

Este comando permite tener salidas tipo tablero de instrumentos de programas donde el valor de una expresión o de una lectura de sensor se actualiza en la misma línea.

DispAty Disp pueden utilizarse dentro del mismo programa.

Nota: El número máximo se establece en 8 ya que coincide con una pantalla llena de líneas en la pantalla del dispositivo portátil, siempre y cuando las líneas no tengan expresiones matemáticas en 2D. El número exacto de líneas depende del contenido de la información mostrada.

Ejemplo

 

 

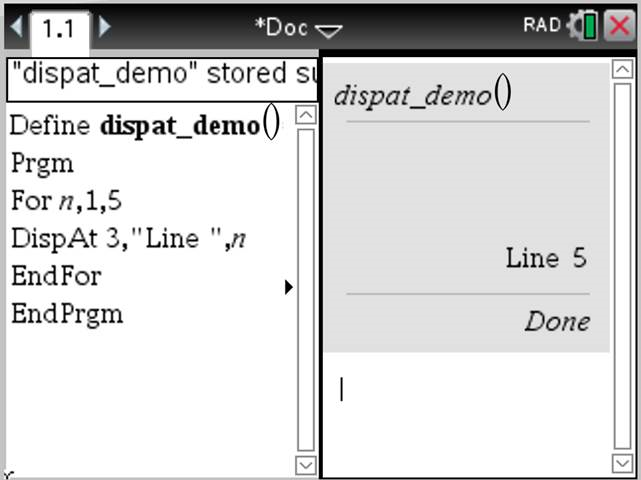
Ejemplos ilustrativos:

Define z()=

Prgm

For n,1,3

DispAt 1, "N: ", n

Disp "Hello"

EndFor

EndPrgm

Salida

z()

Iteration 1:

Line 1: N:1

Line 2: Hello

 

Iteration 2:

Line 1: N:2

Line 2: Hello

Line 3: Hello

 

Iteration 3:

Line 1: N:3

Line 2: Hello

Line 3: Hello

Line 4: Hello

Define z1()=

Prgm

For n,1,3

DispAt 1, "N: ", n

EndFor

 

For n,1,3

Disp "Hello"

EndFor

EndPrgm

z1()

Line 1: N:3

Line 2: Hello

Line 3: Hello

Line 4: Hello

Line 5: Hello

 

Condiciones de error:

Mensaje de error

Descripción

El número de línea de DispAt debe ser entre 1 y 8

La expresión evalúa el número de línea fuera del rango 1 a 8 (inclusive)

Muy pocos argumentos

Le falta uno o más argumentos a la función o al comando.

No hay argumentos

Igual que el cuadro de diálogo actual 'error de sintaxis'

Demasiados argumentos

Limite los argumentos. Mismo error que en Disp.

Tipo de datos no válido

El primer argumento debe ser un número.

Anular: anular DispAt

Un tipo de error datatype "Hello World" se produce para la anulación (si se define la devolución de llamada)

Operador de conversión: DispAt 2_ft @> _m, "Hello World"

CAS: Se produce un tipo de error datatype "Hello World" para la anulación (si se define la devolución de llamada)

Numérico: La conversión se evaluará y si el resultado es un argumento válido, DispAt imprime la cadena en la línea de resultados.

4DMS (4GMS)

Catálogo >

Expr 4DMS

Lista 4DMS

Matriz 4DMS

Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @>DMS.

Interpreta el argumento como un ángulo y despliega el número GMS (GGGGGG¡MM'SS.ss'') equivalente. Vea ¡, ', '' (aquí) para el formato GMS (grado, minutos, segundos).

Nota: 4DMS se convertirá de radianes a grados cuando se use en el modo de Radián. Si la entrada va seguida de un símbolo de grados ¡ , no ocurrirá ninguna conversión. Usted puede usar 4DMS sólo al final de una línea de ingreso.

En modo de ángulo en Grados:

domain() (dominio)

Catálogo >

domain(Expr1, Var)Þexpresión

Devuelve el dominio de Expr1con respecto a Var.

domain() puede utilizarse para examinar los dominios de las funciones. Se restringe a un dominio real y finito.

Esta funcionalidad presenta limitaciones debido a defectos en los algoritmos de simplificación algebráicos para computadora y algoritmos solucionadores.

Algunas funciones no pueden ser utilizadas como argumentos para domain(), sin importar si aparecen explícitamente o dentro de las variables y funciones definidas por el usuario: En el siguiente ejemplo, la expresión no puede simplificarse porque ‰() no es una función permitida.

dominantTerm()

Catálogo >

dominantTerm(Expr1, Var [, Punto])Þexpresión

dominantTerm(Expr1, Var [, Punto]) | Var>Punto Þexpresión

dominantTerm(Expr1, Var [, Punto]) | Var<Punto Þexpresión

Entrega el término dominante de la representación de una serie de potencia de Expr1 expandida alrededor de Punto. El término dominante es aquel cuya magnitud crece con más rapidez cerca de Var = Punto. La potencia resultante de (Var N Punto) puede tener un exponente negativo y/o fraccional. El coeficiente de esta potencia puede incluir logaritmos de (Var N Punto) y otras funciones de Var que están dominadas por todas las potencias de (Var N Punto) teniendo el mismo signo de exponente.

Punto se predetermina a 0. Punto puede ser ˆ o Nˆ, en cuyos casos el término dominante será el término que tiene el exponente más grande de Var en lugar del exponente más pequeño de Var.

dominantTerm(…) entrega “dominantTerm(…)” si no puede determinar tal representación, como para singularidades esenciales como sin(1/z) en z=0, eN1/z en z=0, o ez en z = ˆ o Nˆ.

Si la serie o una de sus derivadas tiene una discontinuidad de salto en un Punto, es probable que el resultado contenga subexpresiones del signo de forma(…) o abs(…) para una variable de expansión real o (-1)piso(…angle(…)…) para una variable de expansión compleja, que es una que termina con “_”. Si usted pretende usar el término dominante sólo para valores en un lado de Punto, entonces anexe a dominantTerm(...) el apropiado de “| Var > Punto”, “| Var < Punto”, “| “Var | Punto” o “Var { Punto” para obtener un resultado más simple.

dominantTerm() se distribuye sobre listas y matrices del 1er argumento.

dominantTerm() es útil cuando usted desea conocer la expresión más simple posible que sea asintótica para otra expresión como Var " Punto. dominantTerm() también es útil cuando no es obvio cuál será el grado del primer término no-cero de una serie, y usted no desea calcular iterativamente, ya sea de manera interactiva o por medio de un bucle de programa.

Nota: Vea también series(), aquí.

dotP() (pPunto)

Catálogo >

dotP(Lista1, Lista2)Þexpresión

Entrega el producto "punto" de dos listas.

dotP(Vector1, Vector2)Þexpresión

Entrega el producto punto" de dos vectores.

Ambos deben ser vectores de fila, o ambos deben ser vectores de columna.