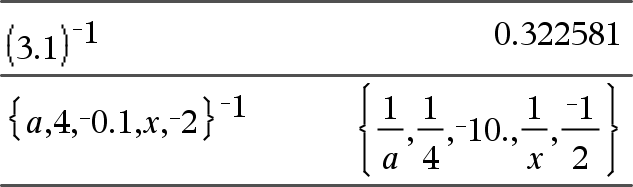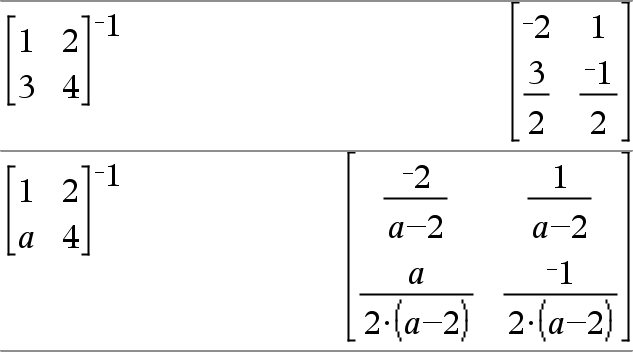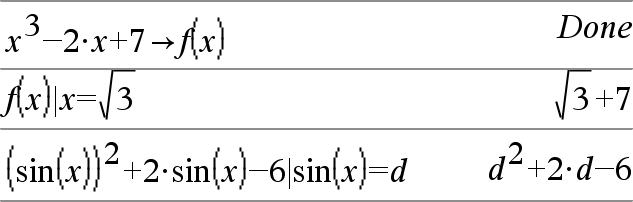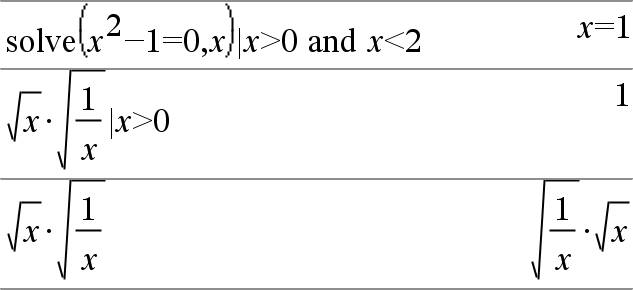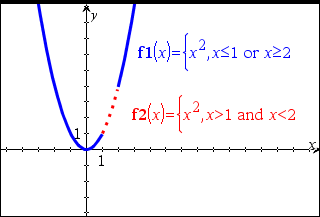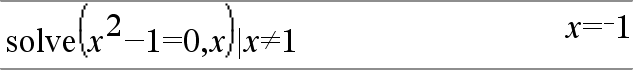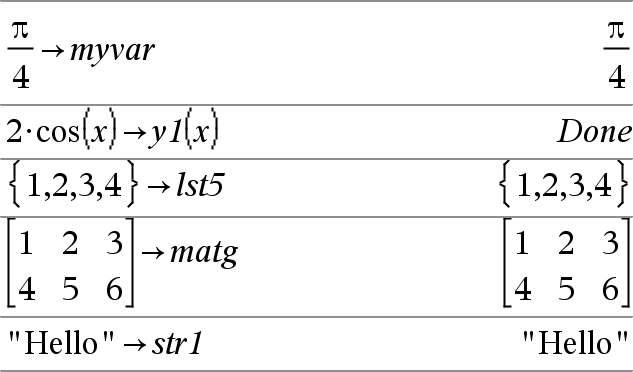|
+ tecla |
|
|
Entrega la suma de los dos argumentos. |
|
|
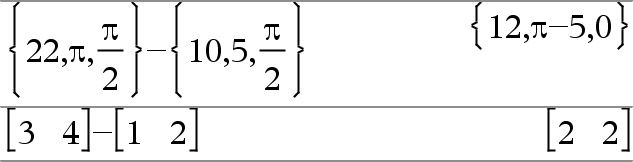
Lista1 + Lista2Þlista Matriz1 + Matriz2Þmatriz Entrega una lista (o matriz) que contiene las sumas de los elementos correspondientes en Lista1 y Lista2 (o Matriz1 y Matriz2). Las dimensiones de los argumentos deben ser iguales. |
|
|
Lista1 + ExprÞlista Entrega una lista que contiene las sumas de Expr y cada elemento en Lista1. |
|
|
Matriz1 + ExprÞmatriz Entrega una matriz con Expr agregada a cada elemento en la diagonal de Matriz1. Matriz1 debe ser cuadrada. Nota: Use .+ (punto más) para agregar una expresión a cada elemento. |
|
|
- tecla |
|
|
Entrega Expr1 menos Expr2. |
|
|
Lista1 N Lista2Þlista Matriz1 N Matriz2Þmatriz Sustrae a cada elemento en Lista2 (o Matriz2) del elemento correspondiente en Lista1 (o Matriz1) y entrega los resultados. Las dimensiones de los argumentos deben ser iguales. |
|
|
Lista1 N ExprÞlista Sustrae a cada elemento de Lista1 de Expr o sustrae Expr de cada elemento de Lista1 y entrega una lista de los resultados. |
|
|
Matriz1 N ExprÞmatriz Expr N Matriz1 entrega una matriz de Expr veces la matriz de identidad menos Matriz1. La Matriz1 debe ser cuadrada. Matriz1 N Expr entrega una matriz de Expr veces la matriz de identidad sustraída de Matriz1. La Matrix1 debe ser cuadrada. Nota: Use .N (punto menos) para sustraer una expresión de cada elemento. |
|
|
r tecla |
|
|
Entrega el producto de los dos argumentos. |
|
|
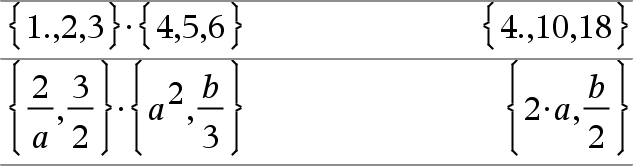
Lista1·Lista2Þlista Entrega una lista que contiene los productos de los elementos correspondientes en Lista1 y Lista2. Las dimensiones de las listas deben ser iguales. |
|
|
Matriz1 ·Matriz2Þmatriz Entrega el producto de la matriz de Matriz1 y Matriz2. El número de columnas en Matriz1 debe igualar el número de filas en Matriz2. |
|
|
Lista1 ·ExprÞlista Entrega una lista que contiene los productos de Expr y cada elemento en Lista1. |
|
|
Matriz1 ·ExprÞmatriz Entrega una matriz que contiene los productos de Expr y cada elemento en Matriz1. Nota: Use .·(punto multiplicar) para multiplicar una expresión por cada elemento. |
|
|
p tecla |
|
|
Entrega el cociente de Expr1 dividido entre Expr2. Nota: Vea también Plantilla de fracciones, aquí. |
|
|
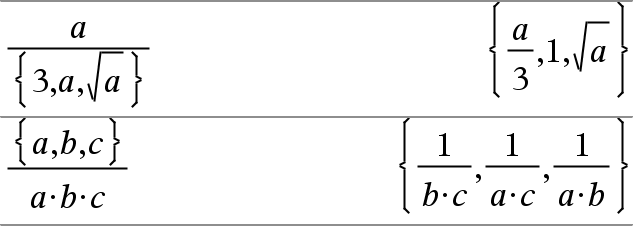
Lista1 à Lista2Þlista Entrega una lista que contiene los cocientes de Lista1 divididos entre Lista2. Las dimensiones de las listas deben ser iguales. |
|
|
Lista1 à Expr Þ lista Entrega una lista que contiene los cocientes de Expr divididos entre Lista1 o deLista1 divididos entre Expr. |
|
|
Entrega una matriz que contiene los cocientes de Matriz1àExpr. Nota: Use . / (punto dividir) para dividir una expresión entre cada elemento. |
|
|
l tecla |
|
|
Lista1 ^ Lista2 Þ lista Entrega el primer argumento elevado a la potencia del segundo argumento. Nota: Vea también Plantilla de exponentes, aquí. Para una lista, entrega los elementos en Lista1 elevados a la potencia de los elementos correspondientes en Lista2. En el dominio real, las potencias fraccionarias que han reducido los exponentes con denominadores impares usan la rama real contra la rama principal para el modo complejo. |
|
|
Entrega Expr elevada a la potencia de los elementos en Lista1. |
|
|
Entrega los elementos en Lista1 elevados a la potencia de Expr. |
|
|
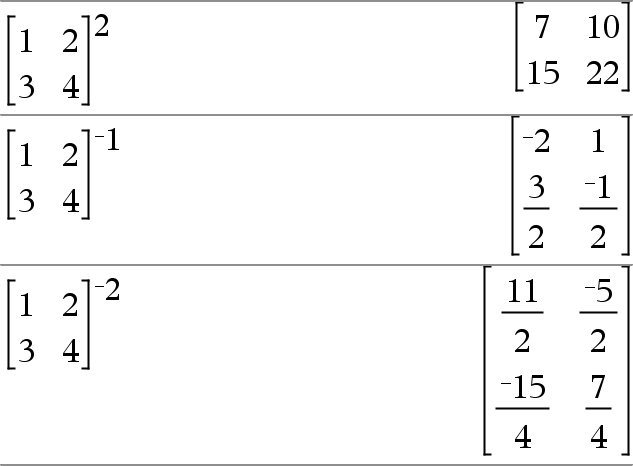
matrizCuadrada1 ^ entero Þ matriz Entrega matrizCuadrada1 elevada a la potencia del entero . matrizCuadrada1 debe ser una matriz cuadrada. Si entero = L1, resuelve la matriz inversa. Si entero < L1, resuelve la matriz inversa a una potencia positiva apropiada. |
|
|
q tecla |
|
|
Entrega el cuadrado del argumento. Lista12 Þ lista Entrega una lista que contiene los cuadrados de los elementos en la Lista1. matrizCuadrada12 Þ matriz Entrega el cuadrado de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el cuadrado de cada elemento. Use .^2 para calcular el cuadrado de cada elemento. |
|
|
^+ teclas |
|
|
Matriz1 .+ Matriz2 Þ matriz Matriz1 .+ Matriz2 entrega una matriz que es la suma de cada par de elementos correspondientes en Matriz1 y Matriz2.
|
|
|
^- teclas |
|
|
Matriz1 .N Matriz2 Þ matriz Matriz1 .NMatriz2 entrega una matriz que es la diferencia entre cada para de elementos correspondientes en Matriz1 y Matriz2.
. |
|
|
^r teclas |
|
|
Matriz1 .· Matriz2 Þ matriz Matriz1 .· Matriz2 entrega una matriz que es el producto de cada par de elementos correspondientes en Matriz1 y Matriz2. |
|
|
^p teclas |
|
|
Matriz1 . / Matriz2 Þ matriz Matriz1 ./ Matriz2 entrega una matriz que es el cociente de cada par de elementos correspondientes en Matriz1 y Matriz2.
. |
|
|
^l teclas |
|
|
Matriz1 .^ Matriz2 Þ matriz Matriz1 .^ Matriz2 entrega una matriz donde cada elemento en Matriz2 es el exponente para el elemento correspondiente en Matriz1.
|
|
|
v tecla |
|
|
LLista1 Þ lista LMatriz1 Þ matriz Entraga la negación del argumento. Para una lista o matriz, entrega todos los elementos negados. Si el argumento es un entero binario o hexadecimal, la negación da el complemento de los dos. |
En modo de base binaria: Importante: Cero, no la letra O
Para ver el resultado completo, presione 5 y después use 7 y 8 para mover el cursor. |
|
/k teclas |
|
|
Lista1 % Þ lista Matriz1 % Þ matriz Entrega Para una lista o matriz, entrega una lista o matriz con cada elemento dividido entre 100. |
Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
|
|
= tecla |
|
|
Expr1 = Expr2Þexpresión Booleana Lista1 = Lista2Þlista Booleana Matriz1 = Matriz2Þmatriz Booleana Entrega verdadero si Expr1 se determina como igual a Expr2. Entrega falso si Expr1 se determina como no igual a Expr2. Cualquier otra cosa entrega una forma simplificada de la ecuación. Para listas y matrices, entrega comparaciones elemento por elemento. Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto. |
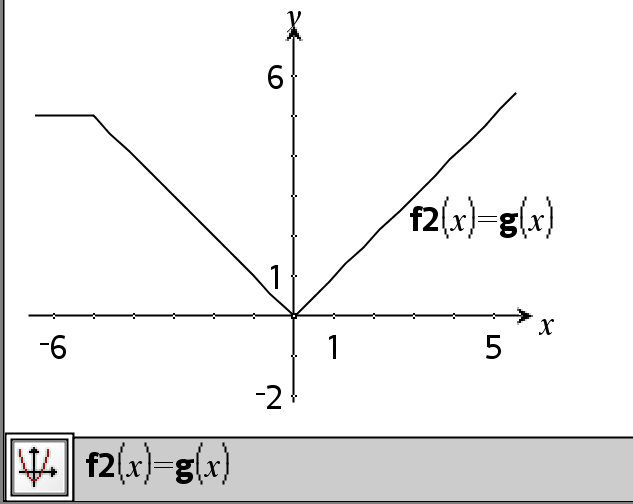
Ejemplo de función que usa símbolos de prueba matemática: =, ƒ, <, {, >, |
Resultado de graficar g(x)
|
|
/= teclas |
|
|
Expr1 ƒ Expr2 Þexpresión Booleana Lista1 ƒ Lista2 Þlista Booleana Matriz1 ƒ Matriz2 Þmatriz Booleana Entrega verdadero si Expr1 se determina como no igual a Expr2. Entrega si Expr1 se determina como igual a Expr2. Cualquier otra cosa entrega una forma simplificada de la ecuación. Para listas y matrices, entrega comparaciones elemento por elemento. Nota: Usted puede insertar este operador desde el teclado al escribir /= |
Vea “=” (igual) ejemplo. |
|
/= teclas |
|
|
Expr1 < Expr2 Þexpresión Booleana Lista1 < Lista2 Þlista Booleana Matriz1 < Matriz2 Þmatriz Booleana Entrega verdadero si Expr1 se determina como menor que Expr2. Entrega falso si Expr1 se determina como mayor que o igual a Expr2. Cualquier otra cosa entrega una forma simplificada de la ecuación. Para listas y matrices, entrega comparaciones elemento por elemento. |
Vea “=” (igual) ejemplo. |
|
/= teclas |
|
|
Expr1 { Expr2 Þexpresión Booleana Lista1 { Lista2 Þlista Booleana Matriz1 { Matriz2 Þmatriz Booleana Entrega verdadero si Expr1 se determina como menor que o igual a Expr2. Entrega falso si Expr1 se determina como mayor que Expr2. Cualquier otra cosa entrega una forma simplificada de la ecuación. Para listas y matrices, entrega comparaciones elemento por elemento. Nota: Usted puede insertar este operador desde el teclado al escribir <= |
Vea “=” (igual) ejemplo. |
|
/= teclas |
|
|
Expr1 > Expr2 Þexpresión Booleana Lista1 > Lista2 Þlista Booleana Matriz1 > Matriz2 Þmatriz Booleana Entrega verdadero si Expr1 se determina como mayor que Expr2. Entrega falso si Expr1 se determina como menor que o igual a Expr2. Cualquier otra cosa entrega una forma simplificada de la ecuación. Para listas y matrices, entrega comparaciones elemento por elemento. |
Vea “=” (igual) ejemplo. |
|
/= teclas |
|
|
Expr1 | Expr2 Þexpresión Booleana Lista1 | Lista2 Þlista Booleana Matriz1 | Matriz2 Þmatriz Booleana Entrega verdadero si Expr1 se determina como mayor que o igual a Expr2. Entrega falso si Expr1 se determina como menor que Expr2. Cualquier otra cosa entrega una forma simplificada de la ecuación. Para listas y matrices, entrega comparaciones elemento por elemento. Nota: Usted puede insertar este operador desde el teclado al escribir >= |
Vea “=” (igual) ejemplo. |
|
teclas /= |
|
|
BooleanaExpr1 Þ BooleanaExpr2 devuelve expresión booleana BooleanaLista1 ÞBooleanaLista2 devuelve lista booleana BooleanaMatriz1 Þ BooleanaMatriz2 devuelvematriz booleana Entero1 ÞEntero2devuelveEntero
Evalúa la expresión Para listas y matrices, devuelve comparaciones elemento por elemento. Nota: Puede insertar este operador con el teclado al escribir => |
|
|
teclas =/ |
|
|
BooleanaExpr1 Û BooleanaExpr2 devuelve expresión booleana BooleanaLista1 Û BooleanaLista2 devuelve lista booleana BooleanaMatriz1 Û BooleanaMatriz2 devuelve matriz booleana Entero1 Û Entero2 devuelve Entero
Devuelve la negación de una Para listas y matrices, devuelve comparaciones elemento por elemento. Nota: Puede insertar este operador con el teclado al escribir <=> |
|
|
º tecla |
|
|
Lista1! Þ lista Matriz1! Þ matriz Entrega el factorial del argumento. Para una lista o matriz, entrega una lista o una matriz de factoriales de los elementos. |
|
|
/k teclas |
|
|
Cadena1 & Cadena2 Þ cadena Entrega una cadena de texto que es Cadena2 adjuntada a Cadena1. |
|
|
Catálogo > |
||||||||||
|
d(Expr1, Var[, Orden])Þexpresión d(Lista1, Var[, Orden])Þlista d(Matriz1, Var[, Orden])Þmatriz Entrega la primera derivada del primer argumento con respecto de la variable Var. Orden, si se incluye, debe ser un entero. Si el orden es menor que cero, el resultado será una antiderivada. Nota: Usted puede insertar esta función desde el teclado al escribir
|
|
|
Catálogo > |
|
|
‰(Expr1, Var[, Baja, Alta]) Þ expresión ‰(Expr1, Var[, Constante]) Þ expresión Entrega la integral de Expr1 con respecto de la variable Var de Baja a Alta. Nota: Vea también Plantilla de integral definida o indefinida, aquí. Nota: Usted puede insertar esta función desde el teclado al escribir integral(...). |
|
|
Si se omiten Baja y Alta , entrega una antiderivada. Se omite una constante simbólica de integración, a menos que usted proporcione el argumento de la Constante . |
|
|
Las antiderivadas igualmente válidas podrían diferir por una constante numérica. Dicha constante podría estar oculta, en particular cuando una antiderivada contiene logaritmos o funciones trigonométricas inversas. Por otra parte, las expresiones constantes de compuesto de variables en ocasiones se agregan para hacer válida una antiderivada sobre un intervalo más grande que la fórmula usual. |
|
|
‰() se entrega a sí mismo para piezas de Expr1 que no puede determinar como una combinación finita explícita de sus funciones y operadores integrados. Cuando usted proporciona Baja y Alta, se hace un intento de localizar cualquier discontinuidad o derivada discontinua en el intervalo Baja < Var < Alta y de subdividir el intervalo en esos lugares. |
|
|
Para la configuración de Auto del modo Auto o Aproximado , se usa la integración numérica donde es aplicable cuando no se puede determinar una antiderivada o un límite. |
|
|
Para la configuración de Aproximado, primero se intenta la integración numérica, si aplica. Las antiderivadas se buscan sólo donde dicha integración numérica no es aplicable o falla. |
Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
|
|
‰() se puede anidar para hacer integrales múltiples. Los límites de la integración pueden depender de las variables de integración afuera de los mismos. Nota: Vea también nInt(), aquí. |
|
|
/q teclas |
|
|
‡ (Lista1)Þlista Entrega la raíz cuadrada del argumento. Para una lista, entrega las raíces cuadradas de todos los elementos en Lista1. Nota: Usted puede insertar esta función desde el teclado al escribir sqrt(...). Nota: Vea también Plantilla de raíz cuadrada, aquí. |
|
|
Catálogo > |
|
|
P(Expr1, Var, Baja, Alta)Þexpresión Nota: Usted puede insertar esta función desde el teclado al escribir prodSeq(...). Evalúa Expr1 para cada valor de Var de Baja a Altay entrega el producto de los resultados. Nota: Vea también Plantilla de producto (P), aquí. |
|
|
P(Expr1, Var, Baja, BajaN1)Þ1 P(Expr1, Var, Baja, Alta) Þ1/P(Expr1, Var, Alta+1, BajaN1) if Alta < BajaN1
Las fórmulas del producto utilizadas se derivan de la siguiente referencia: Ronald L. Graham, Donald E. Knuth y Oren Patashnik. Matemáticas Concretas: Una Fundación para las Ciencias de la Computación. Lectura, Massachusetts: Addison-Wesley, 1994. |
|
|
Catálogo > |
|
|
G(Expr1, Var, Baja, Alta)Þexpresión Nota: Usted puede insertar esta función desde el teclado al escribir secSuma(...). Evalúa Expr1 para cada valor de Var de Baja a Altay entrega la suma de los resultados. Nota: Vea también Plantilla de suma, aquí. |
|
|
G(Expr1, Var, Baja, AltaN1)Þ0 G(Expr1, Var, Baja, Alta) ÞLG(Expr1, Var, Alta+1, BajaN1) si Alta < BajaN1
Las fórmulas de la sumatoria utilizadas se derivan de la siguiente referencia: Ronald L. Graham, Donald E. Knuth y Oren Patashnik. Matemáticas Concretas: Una Fundación para las Ciencias de la Computación. Lectura, Massachusetts: Addison-Wesley, 1994. |
|
|
Catálogo > |
||||||||||
|
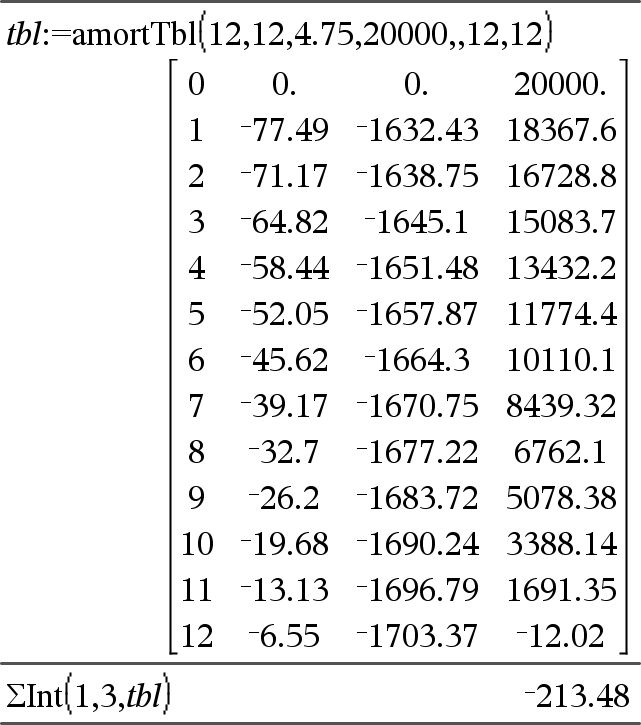
GInt(NPgo1, NPgo2, N, I, VP ,[Pgo], [VF], [PpA], [CpA], [PgoAl], [valorRedondo])Þvalor GInt(NPgo1,NPgo2,tablaAmort)Þvalor La función de amortización que calcula la suma del interés durante un rango de pagos específico. NPgo1 y NPgo2 definen los límites iniciales y finales del rango de pagos. N, I, VP, Pgo, VF, PpA, CpAy PgoAl se describen en la tabla de argumentos de VTD, aquí.
valorRedondo especifica el número de lugares decimales para el redondeo. Predeterminado=2. GInt(NPgo1,NPgo2,tablaAmort) calcula la suma del interés con base en la tabla de amortización tablaAmort. El argumento tablaAmort debe ser una matriz en la forma descrita bajo amortTbl(), aquí. Nota: Vea también GPrn(), abajo y Bal(), aquí. |
|
|
Catálogo > |
||||||||||
|
GPrn(NPgo1, NPgo2, N, I, VP, [Pgo], [VF], [PpA], [CpA], [PgoAl], [valorRedondo])Þvalor GPrn(NPgo1,NPgo2,tablaAmort)Þvalor La función de amortización que calcula la suma del capital durante un rango de pagos específico. NPgo1 y NPgo2 definen los límites iniciales y finales del rango de pagos. N, I, VP, Pgo, VF, PpA, CpAy PgoAl se describen en la tabla de argumentos de VTD, aquí.
valorRedondo especifica el número de lugares decimales para el redondeo. Predeterminado=2. GPrn(NPgo1,NPgo2,tablaAmort) calcula la suma del interés con base en la tabla de amortización tablaAmort. El argumento tablaAmort debe ser una matriz en la forma descrita bajo amortTbl(), aquí. Nota: Vea también GInt(), arriba y Bal(), aquí. |
|
|
/k teclas |
|
|
# cadenaNomVar Se refiere a la variable cuyo nombre es cadenaNomVar. Esto le permite usar cadenas para crear nombres de variable dentro de una función. |
Crea o se refiere a la variable xyz.
Entrega el valor de la variable (r) cuyo nombre se almacena en la variable s1. |
|
i tecla |
|
|
mantisaEexponente Ingresa un número en la notación científica. El número se interpreta como mantisa × 10exponente. Sugerencia: Si usted desea ingresar una potencia de 10 sin causar un resultado de valor decimal, use 10^entero. Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @E. Por ejemplo, escriba 2.3@E4 para ingresar 2.3E4. |
|
|
1 tecla |
|
|
Lista1gÞlista Matriz1gÞmatriz Esta función le proporciona una manera de especificar un ángulo en gradianes mientras está en el modo de Grados o Radianes. En el modo de ángulo en Radianes, multiplica Expr1 por p/200. En el modo de ángulo en Grados, multiplica Expr1 por g/100. En el modo de Gradianes, entrega Expr1 sin cambios. Nota: Usted puede insertar este símbolo desde el teclado de la computadora al escribir @g. |
En modo de Grados, Gradianes o Radianes:
|
|
1 tecla |
|
|
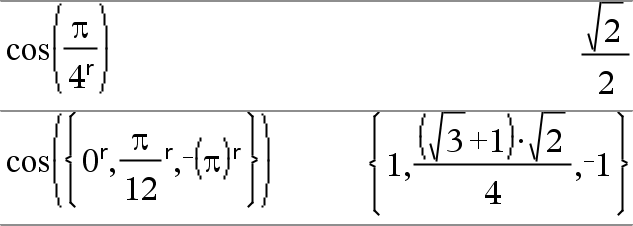
Lista1RÞlista Matriz1RÞmatriz Esta función le proporciona una manera de especificar un ángulo en radianes mientras está en el modo de Grados o Gradianes. En el modo de ángulo en Grados, multiplica el argumento por 180/p. En el modo de ángulo en Radianes, entrega el argumento sin cambios. En el modo de Gradianes, multiplica el argumento por 200/p. Sugerencia: Use R si usted desea forzar los radianes en una definición de función independientemente del modo que prevalece cuando se usa la función. Nota: Usted puede insertar este símbolo desde el teclado de la computadora al escribir @r. |
En modo de ángulo en Grados, Gradianes o Radianes:
|
|
1 tecla |
|
|
Lista1¡Þlista Matriz1¡Þmatriz Esta función le proporciona una manera de especificar un ángulo en grados mientras está en el modo de Gradianes o Radianes. En el modo de ángulo en Radianes, multiplica el argumento por p/180. En el modo de ángulo en Grados, entrega el argumento sin cambios. En el modo de ángulo en Gradianes, multiplica el argumento por 10/9. Nota: Usted puede insertar este símbolo desde el teclado de la computadora al escribir @d. |
En modo de ángulo en Grados, Gradianes o Radianes:
En modo de ángulo en Radianes: Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
|
|
/k teclas |
|||||||
|
gg¡mm'ss.ss''Þexpresión ggUn número positivo o negativo mmUn número no negativo ss.ssUn número no negativo Entrega gg+(mm/60)+(ss.ss/3600). Este formato de ingreso de base‑60 le permite:
Nota: Siga ss.ss con dos apóstrofes (''), no con el símbolo de comillas ("). |
En modo de ángulo en Grados:
|
|
/k teclas |
|
|
[Radio,±q_Ángulo]Þvector (entrada polar) [Radio,±q_Ángulo,Z_Coordenada]Þvector (entrada cilíndrica) [Radio,±q_Ángulo,±q_Ángulo]Þvector (entrada esférica)
Entrega las coordenadas como un vector dependiendo de la configuración del modo del Formato del Vector: rectangular, cilíndrica o esférica. Nota: Usted puede insertar este símbolo desde el teclado de la computadora al escribir @<. |
En el modo de Radianes y en el formato del vector configure a: rectangular
cilíndrico
esférico
|
|
(Magnitud ± Ángulo)ÞvalorComplejo (entrada polar) Ingresa un valor complejo en la forma polar (r±q). El Ángulo se interpreta de acuerdo con la configuración del modo del Ángulo actual. |
En el modo de ángulo en Radianes y el formato complejo Rectangular:
Nota: Para forzar un resultado aproximado, Dispositivo portátil: Presione / ·.
|
|
º tecla |
|
|
variable ' variable '' Ingresa un símbolo primo en una ecuación diferencial. Un símbolo primo sencillo denota una ecuación diferencial de 1er grado, dos símbolos primos denotan una de 2o grado, y así sucesivamente. |
|
|
Vea “Elementos vacíos (inválidos)” , aquí. |
|
|
|
|
|
/_ teclas |
|
|
Expr_Unidad Designa las unidades para una Expr. Todos los nombres de unidad deben comenzar con un guión bajo. Usted puede usar unidades predefinidas o crear sus propias unidades. Para una lista de unidades predefinidas, abra el Catálogo y despliegue la pestaña de Conversiones de Unidades. Usted puede seleccionar nombres de unidades desde el Catálogo o escribir los nombres de unidades directamente. |
Nota: Usted puede encontrar el símbolo de conversión, 4, en el Catálogo. Haga clic en |
|
Variable_ Cuando la Variable no tiene ningún valor, se trata como si representara un número complejo. En forma predeterminada, sin el _ , la variable se trata como real. Si la Variable tiene un valor, el _ se ignora y la Variable retiene su tipo de datos original. Nota: Usted puede almacenar un número complejo para una variable sin usar _ . Sin embargo, para obtener mejores resultados en los cálculos como cSolve() y cZeros(), se recomienda el _. |
Supongamos que z es indefinido:
|
|
/k teclas |
|||||||
|
Expr_Unidad1 4 _Unidad2ÞExpr_Unidad2 Convierte una expresión de una unidad a otra. El caracter de guión bajo _ designa las unidades. Las unidades deben estar en la misma categoría, como Longitud o Área. Para una lista de unidades predefinidas, abra el Catálogo y despliegue la pestaña de Conversiones de Unidades:
Usted también puede escribir los nombres de unidades manualmente. Para escribir “_” cuando escriba nombres de unidades en el dispositivo portátil, presione /_. Nota: Para convertir unidades de temperatura, use tmpCnv() y @tmpCnv(). El operador de conversión 4 no maneja unidades de temperatura. |
|
|
Catálogo > |
|
|
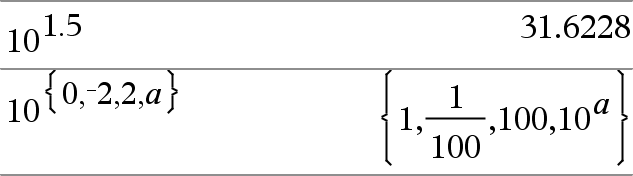
10^ (Expr1)Þexpresión 10^ (Lista1)Þlista Entrega 10 elevado a la potencia del argumento. Para una lista, entrega 10 elevado a la potencia de los elementos en Lista1. |
|
|
10^(matrizCuadrada1)ÞmatrizCuadrada Entrega 10 elevado a la potencia de matrizCuadrada1. Esto no es lo mismo que calcular 10 elevado a la potencia de cada elemento. Para obtener información acerca del método de cálculo, consulte cos(). matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante. |
|
|
Catálogo > |
|
|
Lista1 ^/Þlista Entrega el recíproco del argumento. Para una lista, entrega los recíprocos de los elementos en Lista1. |
|
|
matrizCuadrada1 ^/ÞmatrizCuadrada Entrega el inverso de matrizCuadrada. matrizCuadrada1 debe ser una matriz cuadrada no singular. |
|
|
teclas /k |
||||||||||
|
Expr | BooleanaExpr1 [ Expr | BooleanaExpr1 [ El símbolo de restricción ("|") funciona como un operador binario. El operando a la izquierda de | es una expresión. El operando a la derecha de | especifica una o más relaciones que deben afectar la simplificación de la expresión. Las relaciones múltiples luego de | deben estar unidas por "and" lógica u operadores "or". El operador restrictivo proporciona tres funciones básicas:
|
|
|||||||||
|
Las sustituciones tienen la forma de una igualdad, tal como x=3 o y=sin(x). Para ser más efectiva, el lado izquierdo debe ser una variable simple. Expr | Variable = el valorsustituirá el valor para cada ocurrencia de la Variable en la Expr. |
|
|||||||||
|
Las restricciones de intervalo tienen la forma de una o más desigualdades unidas por "and" lógica u operadores "or". Las restricciones de intervalo también permite la simplificación que de otro modo sería inválida o no computable. |
|
|||||||||
|
Las exclusiones utilizan el operador relacional "distinto" (/= o ƒ) para no tener en cuenta un valor específico. |
|
|
/h tecla |
|
|
Lista & Var Matriz & Var Expr & Función(Parám1,...) Lista & Función(Parám1,...) Matriz & Función(Parám1,...) Si la variable Var no existe, la crea y la inicializa para Expr, Listao Matriz. Si la variable Var ya existe y no está bloqueada o protegida, reemplaza sus contenidos con Expr, Listao Matriz. Sugerencia: Si usted planea hacer cómputos simbólicos al usar variables indefinidas, evite almacenar cualquier cosa en las variables de una letra utilizadas comúnmente como a, b, c, x, y, z, y así sucesivamente. Nota: Usted puede insertar este operador desde el teclado al escribir =: como un acceso directo. Por ejemplo, escriba pi/4=: myvar. |
|
|
/t teclas |
|
|
Var := Lista Var := Matriz Función(Parám1,...) := Expr Función(Parám1,...) := Lista Función(Parám1,...) := Matriz Si la variable Var no existe, crea Var y la inicializa para Expr, Listao Matriz. Si Var ya existe y no está bloqueada o protegida, reemplaza sus contenidos con Expr, Listao Matriz.
|
|
|
/k teclas |
|
|
© [texto] © procesa texto como una línea de comentario, lo que le permite anotar funciones y programas que usted crea. © puede estar al comienzo y en cualquier parte en la línea. Todo a la derecha de ©, al final de la línea, es el comentario. Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto. |
|
|
0B teclas, 0H teclas |
|
|
0b númeroBinario 0h númeroHexadecimal Denota un número binario o hexadecimal, respectivamente. Para ingresar un número binario o hexadecimal, usted debe ingresar el prefijo 0b ó 0h independientemente del modo de la Base. Sin un prefijo, un número se trata como decimal (base 10). Los resultados se despliegan de acuerdo con el modo de la Base. |
En modo de base decimal:
En modo de base binaria:
En modo de base hexadecimal:
|








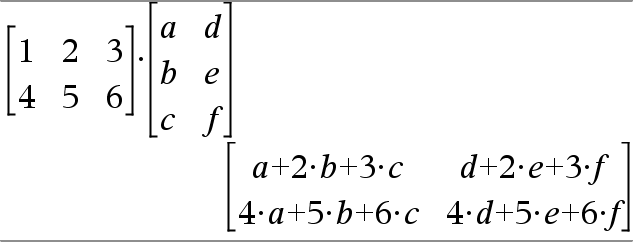












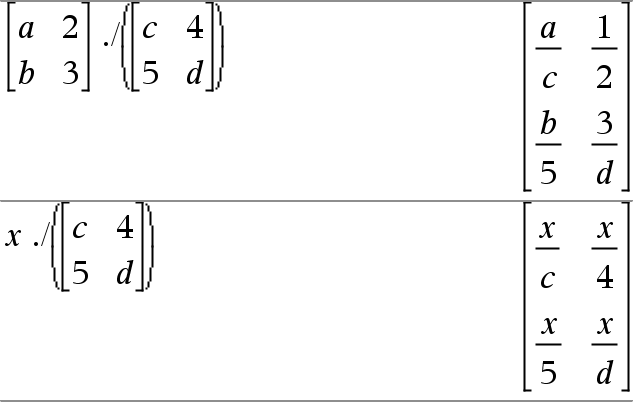

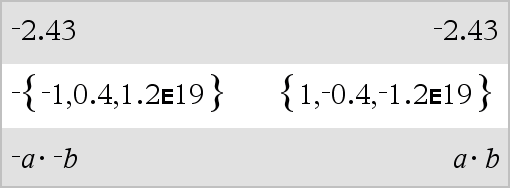
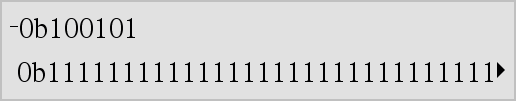
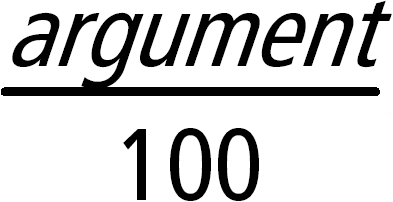
 .
.


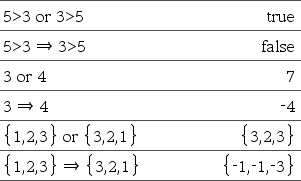
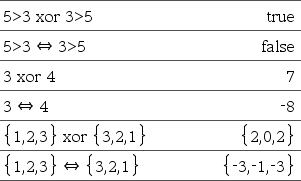



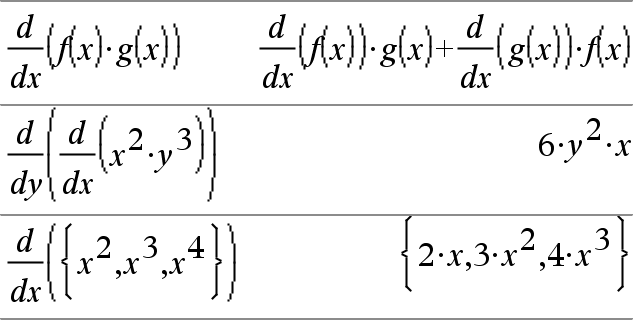


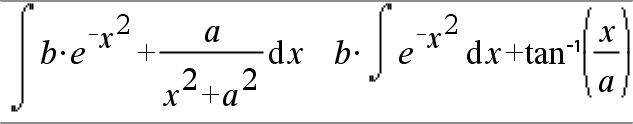

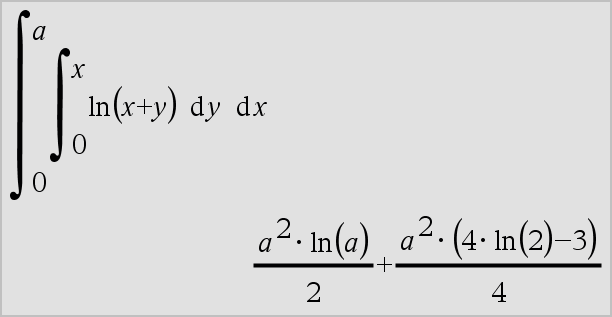

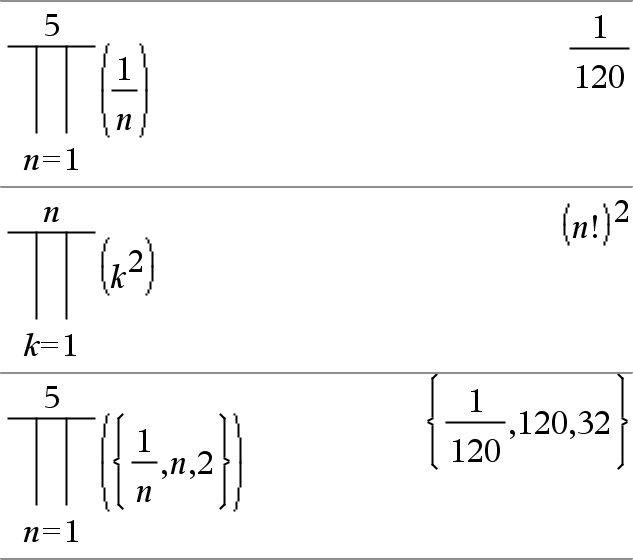

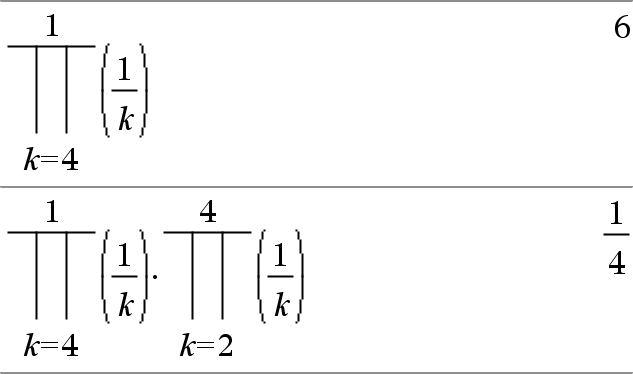
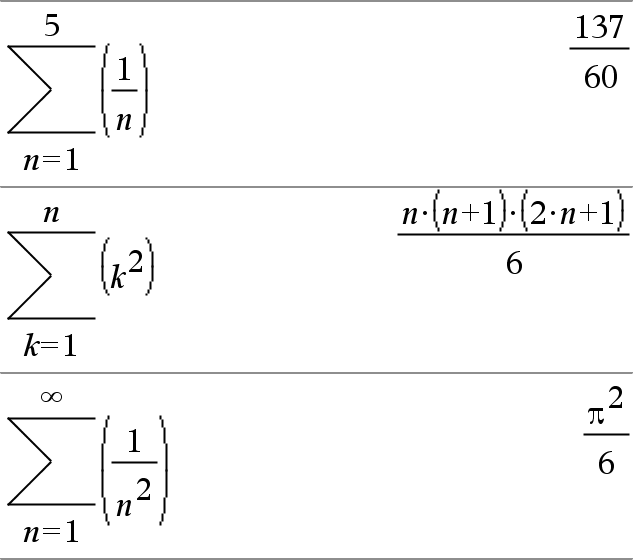

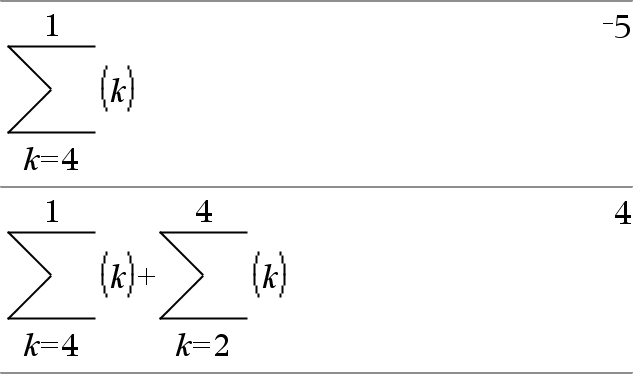
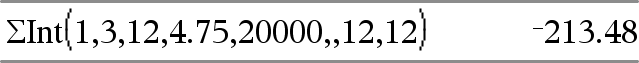
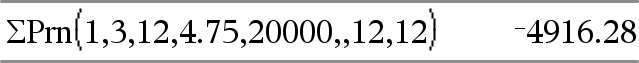






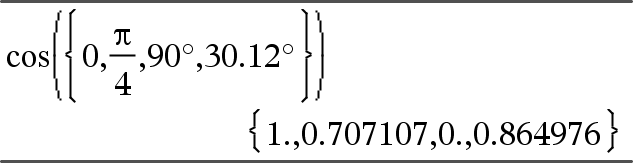

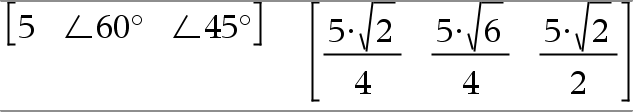
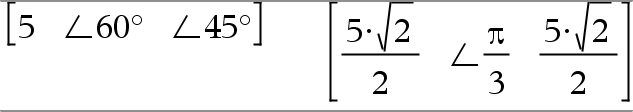

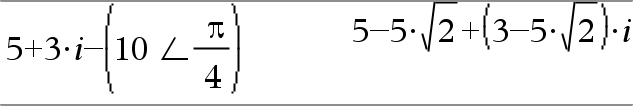
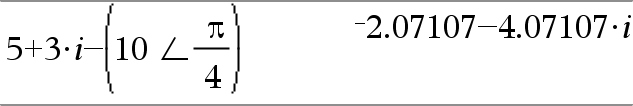
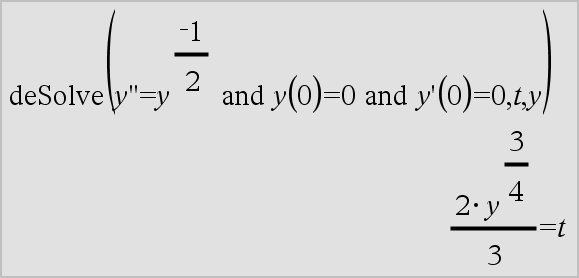

 y luego haga clic en
y luego haga clic en