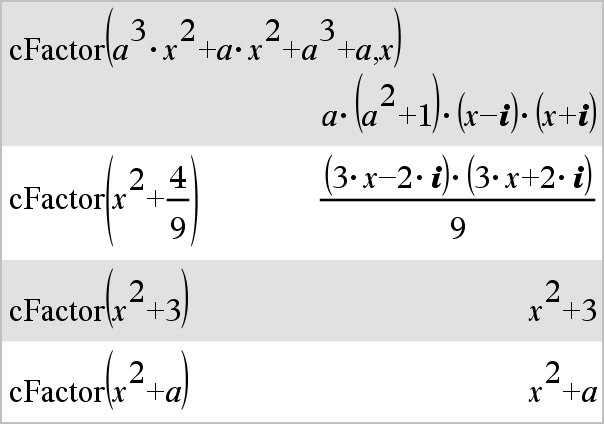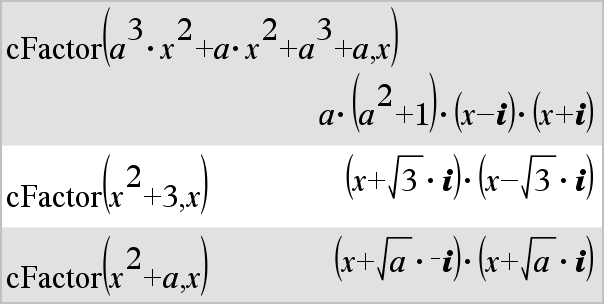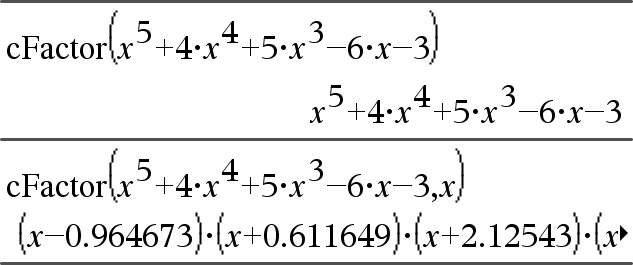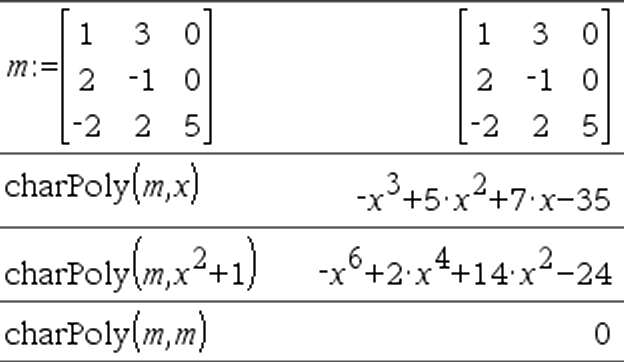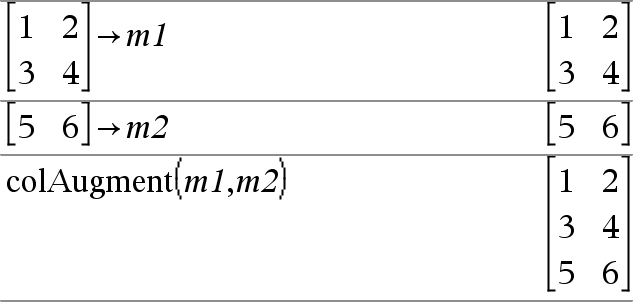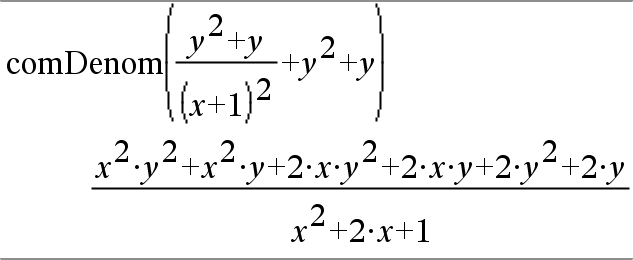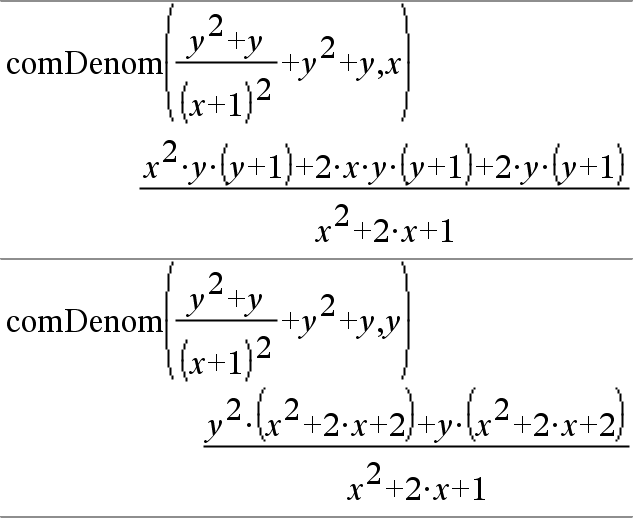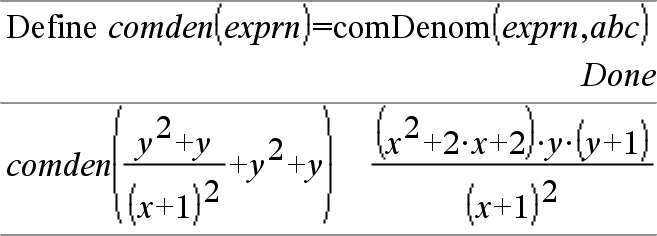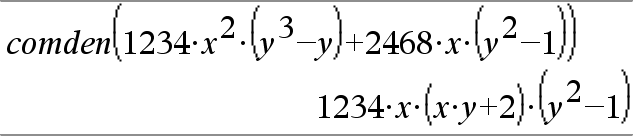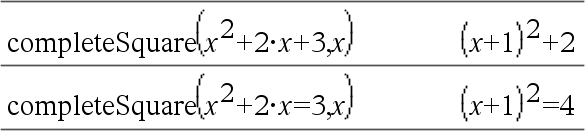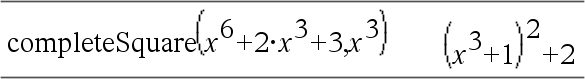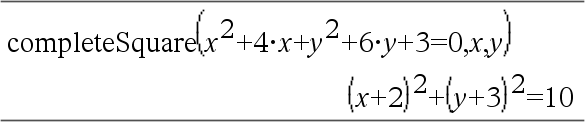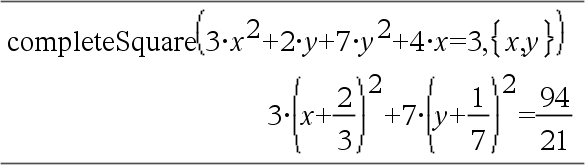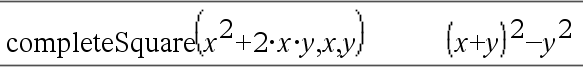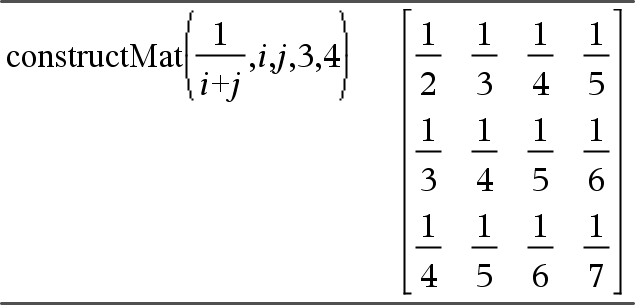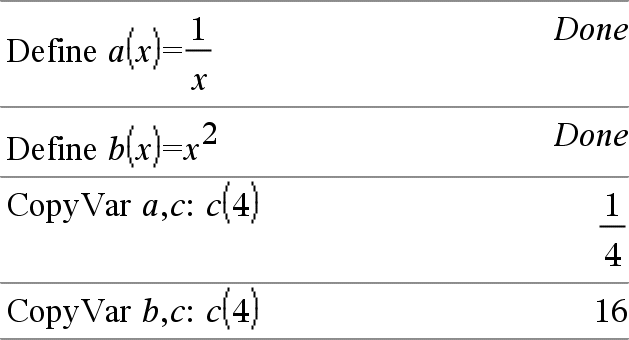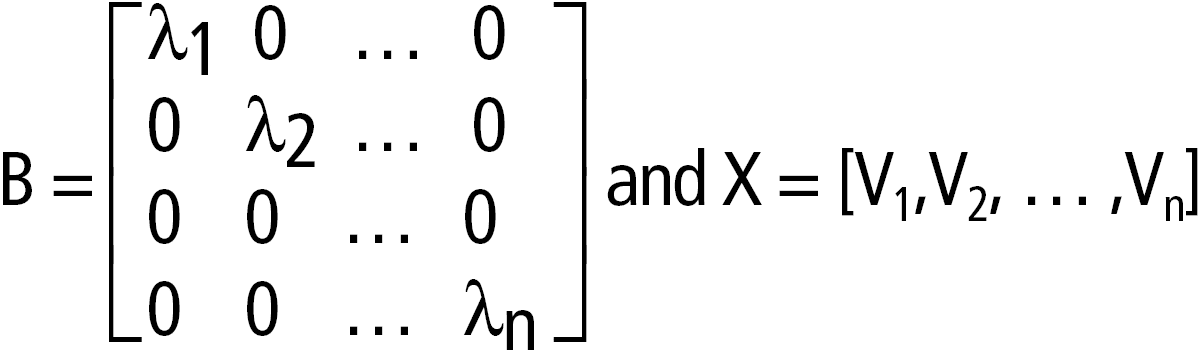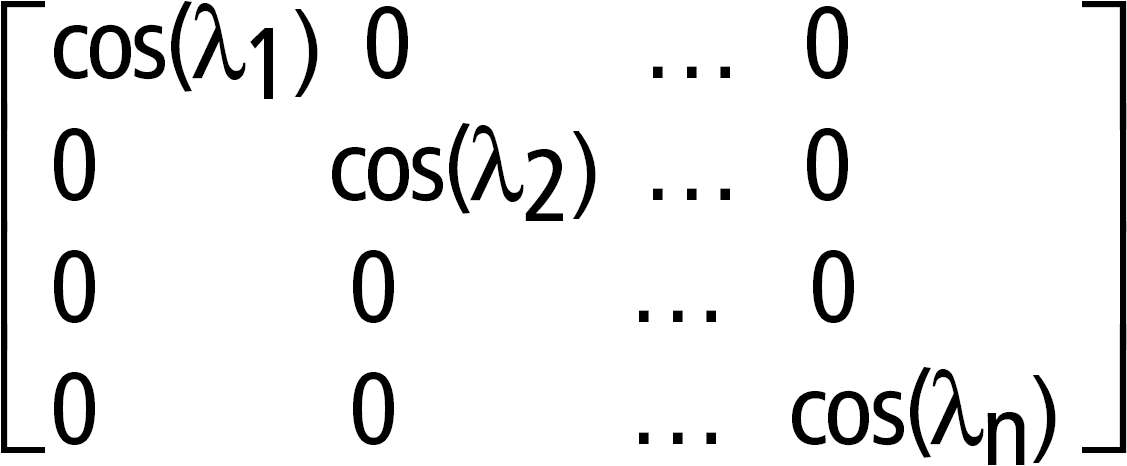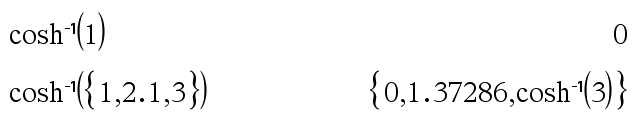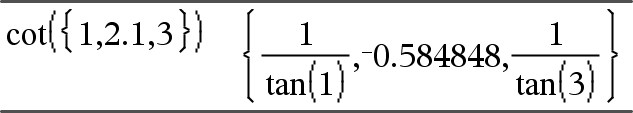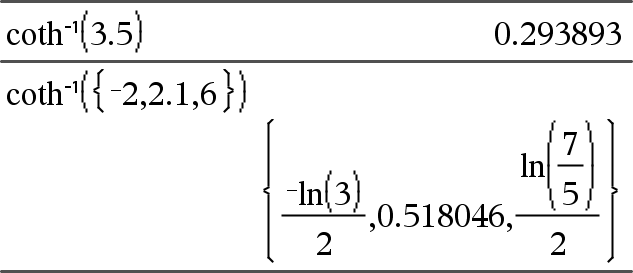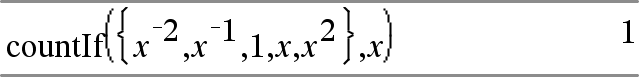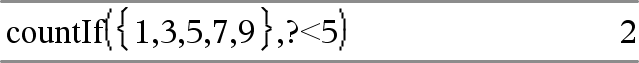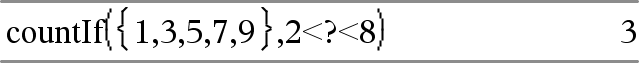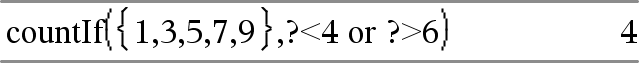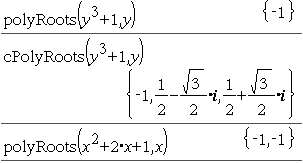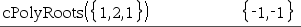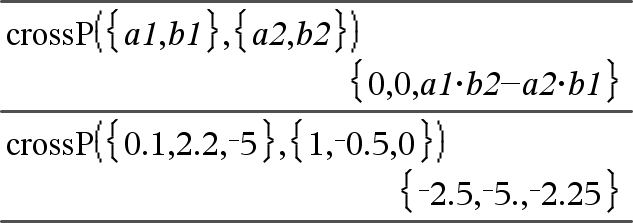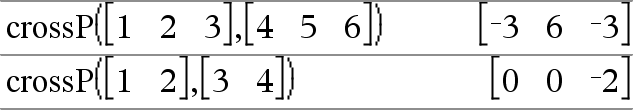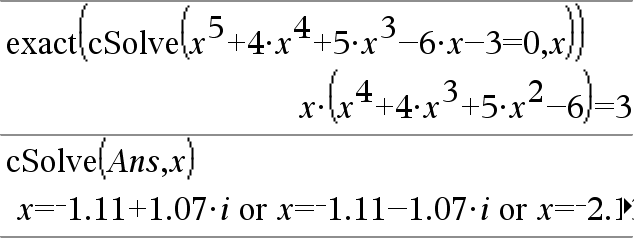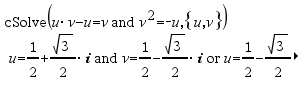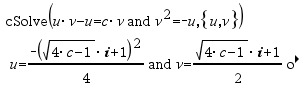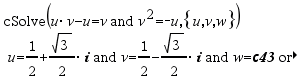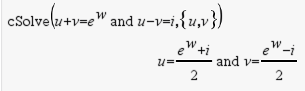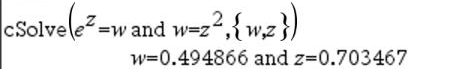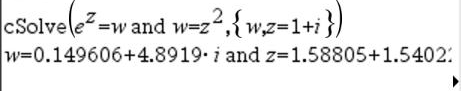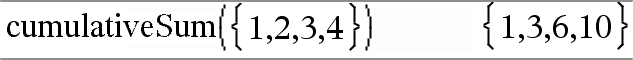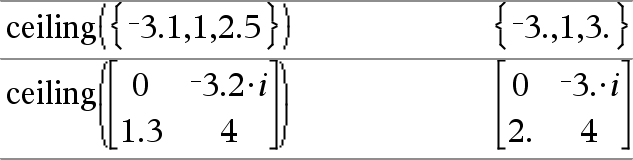
ceiling(Lista1)Þlista

ceiling(Matriz1)Þmatriz

Entrega una lista o matriz del techo de cada elemento.

centralDiff(Expr1,Var [=Valor][,Paso])Þexpresión

centralDiff(Expr1,Var [,Paso])|Var=ValorÞexpresión

centralDiff(Expr1,Var [=Valor][,Lista])Þlista

centralDiff(Lista1,Var [=Valor][,Paso])Þlista

centralDiff(Matriz1,Var [=Valor][,Paso])Þmatriz

Entrega la derivada numérica usando la fórmula del cociente diferencial central.

Cuando se especifica el Valor, se eliminan todas las asignaciones anteriores de la variable o cualquier sustitución "|" para la variable.

Paso es el valor del paso. Si se omite Paso , se predetermina a 0.001.

Al usar Lista1 o Matriz1, la operación se mapea a lo largo de los valores en la lista y a lo largo de los elementos de la matriz.

Nota: Vea también avgRC() y d().

Para la configuración automática del modo Auto o Aproximado , incluyendo Var , también permite la aproximación con coeficientes de punto flotante, donde los coeficientes irracionales no se pueden expresar en forma explícita concisamente en términos de funciones integradas. Incluso cuando hay sólo una variable, incluyendo Var , puede producir una factorización más completa.

Nota: Vea también factor().

char(Entero)Þcaracter

Entrega una cadena de caracteres que contiene el caracter numerado Entero desde el conjunto de caracteres del dispositivo portátil. El rango válido para Entero es 0–65535.

charPoly(matrizCuadrada,Var)Þexpresión polinómica

charPoly(matrizCuadrada,Expr)Þexpresión polinómica

charPoly(matrizCuadrada1,Matriz2)Þexpresión polinómica

Entrega el polinomio característico de matrizCuadrada. El polinomio característico de n×n matriz A, denotado por pA(l), es el polinomio definido por

pA(l) = det(l• I NA)

donde I denota la matriz de identidad n×n .

matrizCuadrada1 y matrizCuadrada2 deben tener dimensiones iguales.

c22way matrizObs

chi22way matrizObs

Resuelve una prueba c2 para la asociación en la tabla bidireccional de conteos en la matriz observada matrizObs. Un resumen de resultados se almacena en la variable stat.results (aquí).

Para obtener información sobre el efecto de los elementos vacíos en una matriz, vea “Elementos vacíos (inválidos)” (aquí).

c2Cdf(límiteInferior,límiteSuperior,df)Þnúmero si límiteInferior y límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

chi2Cdf(límiteInferior,límiteSuperior,df)Þnúmero si límiteInferior y límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

Genera la probabilidad de distribución c2 entre límiteInferior y límiteSuperior para grados específicos de libertad df.

Para P(X { límiteSuperior), configure límiteInferior = 0.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (aquí).

c2GOF listaObs,listaExp,df

chi2GOF listaObs,listaExp,df

Realiza una prueba para confirmar que los datos de la muestra son de una población que cumple con una distribución especificada. listaObs es una lista de conteos y debe contener enteros. Un resumen de resultados se almacena en la variable stat.results (aquí).

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (aquí).

c2Pdf(XVal,df)Þnúmero si XVal es un número, lista si XVal es una lista

chi2Pdf(XVal,df)Þnúmero si XVal es un número, lista si XVal es una lista

Genera la función de densidad de probabilidad (pdf) para la distribución c2 a un valor especificado XVal para los grados de libertad especificados df.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (aquí).

ClearAZ

Limpia todas las variables de caracter único en el espacio del problema actual.

Si una o más de las variables están bloqueadas, este comando despliega un mensaje de error y borra únicamente las variables no bloqueadas. Vea unLock, aquí.

ClrErr

Limpia el estado del error y configura Codigerr de la variable del sistema a cero.

La cláusula Else del bloque Try...Else...EndTry debe usar ClrErr o PassErr. Si el error se debe procesar o ignorar, use ClrErr. Si no se sabe qué hacer con el error, use PassErr para enviarlo al siguiente manipulador de errores. Si no hay ningún otro manipulador de errores Try...Else...EndTry pendiente, el cuadro de diálogo de error se desplegará como normal.

Nota: Vea también PasErr, aquí, y Try, aquí.

Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

colAugment(Matriz1, Matriz2)Þmatriz

Entrega una nueva matriz que es Matriz2 adjuntada a Matriz2. Las matrices deben tener dimensiones de columna iguales, y Matriz2 se adjunta a Matriz1 como nuevas filas. No altera Matriz1 o Matriz2.

colDim(Matriz)Þexpresión

Entrega el número de columnas contenidas en Matriz.

Nota: Vea también rowDim().

colNorm(Matriz)Þexpresión

Entrega el máximo de las sumas de los valores absolutos de los elementos en las columnas en Matriz.

Nota: Los elementos de matriz indefinida no están permitidos. Vea también rowNorm().

Incluso cuando no hay ningún denominador, la función comden es con frecuencia una manera rápida de lograr la factorización parcial si factor() es demasiado lento o si se agota la memoria.

Sugerencia: Ingrese esta definición de la función comden() y pruébela en forma rutinaria como una alternativa para comDenom() y factor().

completeSquare(ExprOEcn, Var) expresión o ecuación Þ

completeSquare(ExprOEcn, Var^Potencia) expresión o ecuación Þ

completeSquare(ExprOEcn, Var1, Var2 [,...])expresión o ecuación Þ

completeSquare(ExprOEcn, {Var1, Var2 [,...]})expresión o ecuación Þ

Convierte una expresión polinomial cuadrática de la forma a·x2+b·x+c en la forma a·(x-h)2+k

- o -

Convierte una ecuación cuadrática de la forma a·x2+b·x+c=d en la forma a·(x-h)2=k

El primer argumento debe ser una expresión o ecuación cuadrática en forma estándar con respecto del segundo argumento.

El Segundo argumento debe ser un término de una variable sencilla o un término de una variable sencilla elevado a una potencia racional, por ejemplo x, y2 o z(1/3).

La tercera y cuarta sintaxis intentan completar el cuadrado con respecto de las variables Var1, Var2 [,… ]).

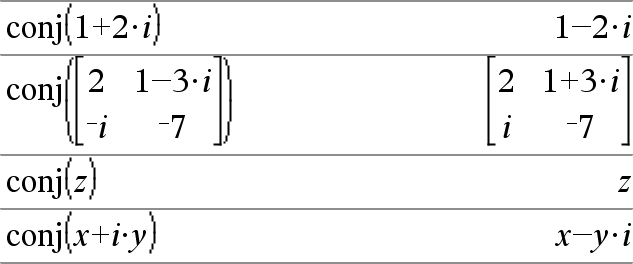
conj(Expr1)Þexpresión

conj(Lista1)Þlista

conj(Matriz1)Þmatriz

Entrega el complejo conjugado del argumento.

Nota: Todas las variables indefinidas se tratan como variables reales.

constructMat(Expr,Var1,Var2,numFilas,numCols) Þmatriz

Entrega una matriz basada en los argumentos.

Expr es una expresión en las variables Var1 y Var2. Los elementos en la matriz resultante se forman al evaluar Expr para cada valor incrementado de Var1 y Var2.

Var1 se incrementa automáticamente desde 1 a numFilas. Dentro de cada fila, Var2 se incrementa desde 1 a numCols.

CopyVar Var1., Var2. copia todos los miembros del grupo de la variable Var1. al grupo Var2. , creando Var2. si es necesario.

Var1. debe ser el nombre de un grupo de variables existente, como los resultados de las estadísticas stat.nn o las variables creadas usando la función LibShortcut() . Si Var2. ya existe, este comando reemplaza todos los miembros que son comunes para ambos grupos y agrega los miembros que no existen todavía. Si uno o más miembros de Var2. están bloqueados, todos los miembros de Var2. se dejan sin cambios.

corrMat(Lista1,Lista2[,…[,Lista20]])

Genera la matriz de correlación para la matriz aumentada [Lista1, Lista2, ..., Lista20].

Expr 4cos

Nota: Se puede insertar este operador desde el teclado de la computadora al escribir @>cos.

Representa Expr en términos de coseno. Este es un operador de conversión de despliegue. Se puede usar únicamente al final de la línea de ingreso.

4cos reduce todas las potencias de sin(...) módulo 1Ncos(...)^2 de manera que cualquier potencia restante de cos(...) tiene exponentes en el rango (0, 2). Entonces, el resultado estará libre de sin(...) si y sólo si sin(...) ocurre en la expresión dada únicamente para potencias iguales.

Nota: Este operador de conversión no está soportado en los modos de Ángulo en Grados o Gradianes. Antes de usarlo, asegúrese de que el modo de Ángulo está configurado a Radianes y que Expr no contiene referencias explícitas para ángulos en grados o gradianes.

cos(matrizCuadrada1)ÞmatrizCuadrada

Entrega el coseno de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el coseno de cada elemento.

Cuando una función escalar f(A) opera en matrizCuadrada1 (A), el resultado se calcula por medio del algoritmo:

Compute los valores propios (li) y los vectores propios (Vi) de A.

matrizCuadrada1 debe ser diagonalizable. Asimismo, no puede tener variables simbólicas a las que no se ha asignado un valor.

Forme las matrices:

Luego A = X B X/y f(A) = X f(B) X/. Por ejemplo, cos(A) = X cos(B) X/ donde:

cos(B) =

Todos los cálculos se realizan usando aritmética de punto flotante.

cos/(matrizCuadrada1)ÞmatrizCuadrada

Entrega el coseno inverso de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el coseno inverso de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante.

cosh(matrizCuadrada1)ÞmatrizCuadrada

Entrega el coseno hiperbólico de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el coseno hiperbólico de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante.

cosh/(matrizCuadrada1)ÞmatrizCuadrada

Entrega el coseno hiperbólico inverso de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el coseno hiperbólico inverso de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante.

cot(Expr1) Þ expresión

cot(Lista1) Þ lista

Entrega la cotangente de Expr1 o entrega una lista de cotangentes de todos los elementos en Lista1.

Nota: El argumento se interpreta como un ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual. Se puede usar ¡, G o R para anular el modo de ángulo en forma temporal.

cot/(Expr1)Þexpresión

cot/(Lista1)Þlista

Entrega el ángulo cuya cotangente es Expr1 o entrega una lista que contiene las cotangentes inversas de cada elemento de Lista1.

Nota: El resultado se entrega como un ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual.

Nota: Se puede insertar esta función desde el teclado al escribir arccot(...).

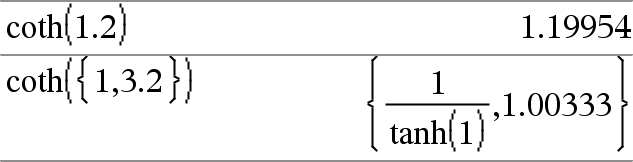
coth(Expr1)Þexpresión

coth(Lista1)Þlista

Entrega la cotangente hiperbólica de Expr1 o entrega una lista de cotangentes hiperbólicas de todos los elementos de Lista1.

coth/(Expr1)Þexpresión

coth/(Lista1)Þlista

Entrega la cotangente hiperbólica inversa de Expr1 o entrega una lista que contiene las cotangentes hiperbólicas inversas de cada elemento de Lista1.

Nota: Se puede insertar esta función desde el teclado al escribir arccoth(...).

count(Valor1oLista1 [,Valor2oLista2 [,...]])Þvalor

Entrega el conteo acumulado de todos los elementos en los argumentos que se evalúan a valores numéricos.

Cada argumento puede ser una expresión, valor, lista o matriz. Se puede mezclar tipos de datos y usar argumentos de varias dimensiones.

Para una lista, matriz o rango de celdas, cada elemento se evalúa para determinar si se debe incluir en el conteo.

Dentro de la aplicación Listas y Hoja de Cálculo, se puede usar un rango de celdas en lugar de cualquier argumento.

Los elementos vacíos (anulados) se ignoran. Para obtener más información sobre elementos vacíos, vea aquí.

countif(Lista,Criterios)Þvalor

Entrega el conteo acumulado de todos los elementos en Lista que cumplen con los Criteriosespecificados.

Los criterios pueden ser:

Dentro de la aplicación Listas y Hoja de Cálculo, se puede usar un rango de celdas en lugar de Lista.

Los elementos vacíos (anulados) en la lista se ignoran. Para obtener más información sobre elementos vacíos, vea aquí.

Nota: Vea también sumIf(), aquí, y frequency(), aquí.

cPolyRoots(Poli,Var)Þlista

cPolyRoots(ListaDeCoefs)Þlista

La primera sintaxis, cPolyRoots(Poli,Var), entrega una lista de raíces complejas del polinomio Poli con respecto de la variable Var.

Poli debe ser un polinomio en una variable.

La segunda sintaxis, cPolyRoots(ListaDeCoefs), entrega una lista de raíces complejas para los coeficientes en ListaDeCoefs.

Nota: Vea también polyRoots(), aquí.

crossP(Vector1, Vector2)Þvector

Entrega un vector de fila o columna (dependiendo de los argumentos) que es el producto cruzado de Vector1 y Vector2.

Tanto Vector1 como Vector2 deben ser vectores de fila, o ambos deben ser vectores de columna. Ambos vectores deben tener una dimensión igual, y la dimensión debe ser 2 ó 3.

csc(Expr1)Þexpresión

csc(Lista1)Þlista

Entrega la cosecante de Expr1 o entrega una lista que contiene las cosecantes de todos los elementos en Lista1.

csc/(Expr1) Þ expresión

csc/(Lista1) Þ lista

Entrega el ángulo cuya cosecante es Expr1 o entrega una lista que contiene las cosecantes inversas de cada elemento de Lista1.

Nota: El resultado se entrega como un ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual.

Nota: Se puede insertar esta función desde el teclado al escribir arccsc(...).

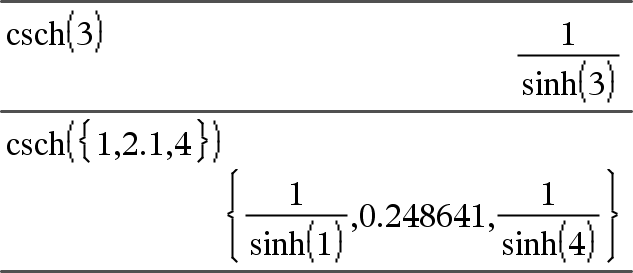
csch(Expr1)Þexpresión

csch(Lista1) Þ lista

Entrega la cosecante hiperbólica de Expr1 o entrega una lista de cosecantes hiperbólicas de todos los elementos de Lista1.

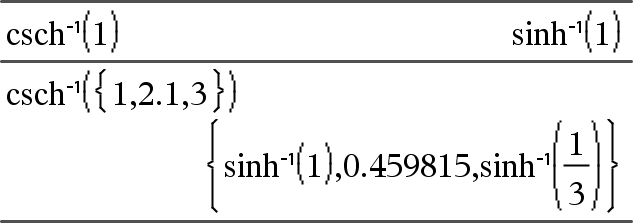
csch/(Expr1) Þ expresión

csch/(Lista1) Þ lista

Entrega la cosecante hiperbólica inversa de Expr1 o entrega una lista que contiene las cosecantes hiperbólicas inversas de cada elemento de Lista1.

Nota: Se puede insertar esta función desde el teclado al escribir arccsch(...).

Con frecuencia es necesario un cálculo irreal para determinar una solución irreal. Por convergencia, un cálculo podría tener que ser más bien cercano a una solución.

CubicReg X, Y[, [Frec] [, Categoría, Incluir]]

Resuelve la regresión polinómica cúbicay = a·x3+b· x2+c·x+den listas X y Y con frecuencia Frec. Un resumen de resultados se almacena en la variable stat.results (aquí).

Todas las listas deben tener una dimensión igual, excepto por Incluir.

X y Y son listas de variables independientes y dependientes.

Frec es una lista opcional de valores de frecuencia. Cada elemento en Frec especifica la frecuencia de la ocurrencia para cada punto de datos X y Y correspondientes. El valor predeterminado es 1. Todos los elementos deben ser enteros | 0.

Categoría es una lista de códigos de categoría para los datos X y Y correspondientes.

Incluir es una lista de uno o más códigos de categoría. Sólo aquellos elementos de datos cuyo código de categoría está incluido en esta lista están incluidos en el cálculo.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (aquí).

cumulativeSum(Matriz1)Þmatriz

Entrega una matriz de sumas acumulativas de los elementos en Matriz1. Cada elemento está en la suma acumulativa de la columna desde la parte superior hasta ha parte inferior.

Un elemento vacío (anulado) en Lista1 o Matriz1 produce un elemento anulado en la lista o matriz resultante. Para obtener más información sobre elementos vacíos, vea aquí.

Cycle

Transfiere el control de inmediato a la siguiente iteración del bucle actual (For, While, o Loop).

Cycle no está permitido afuera de las tres estructuras de bucles ((For, While, o Loop).

Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Vector 4Cylind

Nota: Se puede insertar este operador desde el teclado de la computadora al escribir @>Cylind.

Despliega el vector de fila o columna en forma cilíndrica [r,±q, z].

Vector debe tener exactamente tres elementos. Puede ser una fila o una columna.

Con frecuencia es necesario un cálculo irreal para determinar un cero irreal. Por convergencia, un cálculo podría tener que ser más bien cercano a un cero.