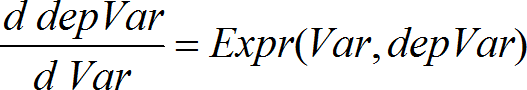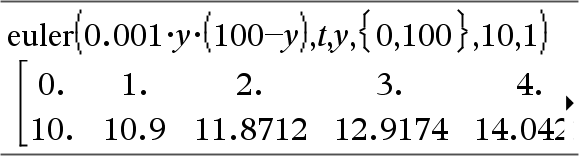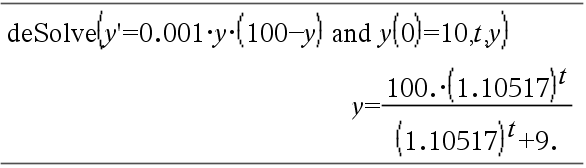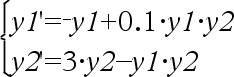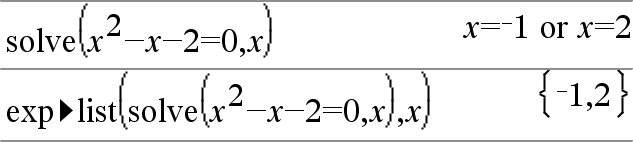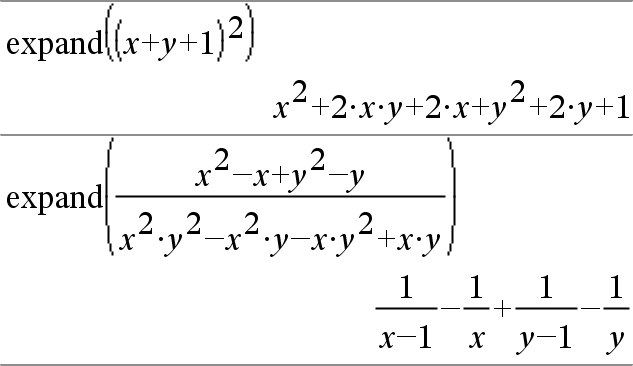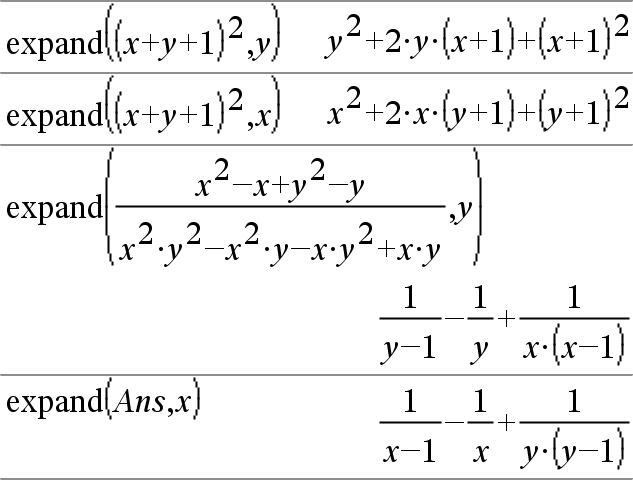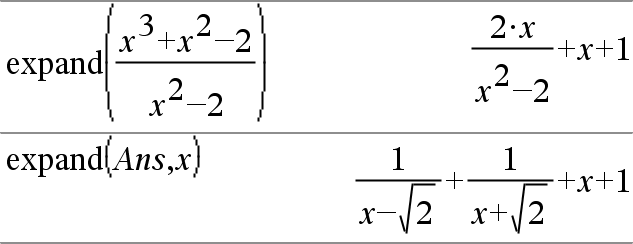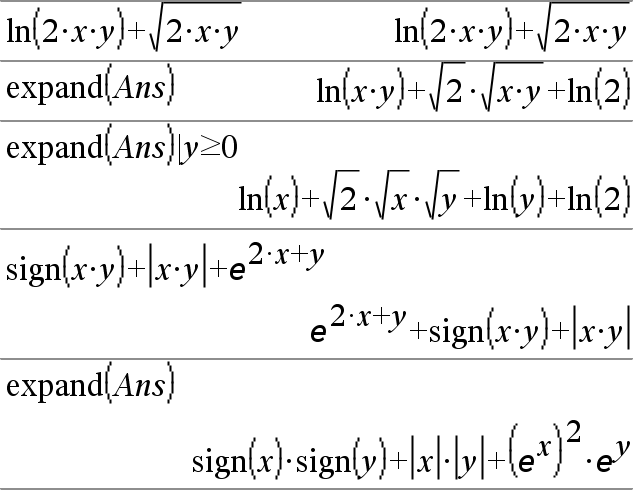e^(matrizCuadrada1)ÞmatrizCuadrada

Entrega el exponencial de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular e elevado a la potencia de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante.

eff(tasaNominal,CpA)Þvalor

Función financiera que convierte la tasa de interés nominal tasaNominal en una tasa efectiva anual, donde CpA se da como el número de periodos de capitalización por año.

tasaNominal debe ser un número real y CpA debe ser un número real > 0.

Nota: Vea también nom(), aquí.

eigVc(matrizCuadrada)Þmatriz

Entrega una matriz que contiene los vectores propios para una matrizCuadradareal o compleja, donde cada columna en el resultado corresponde a un valor propio. Tome en cuenta que un vector propio no es único; puede escalarse por medio de cualquier factor constante. Los vectores propios se normalizan, lo que significa que si V = [x1, x2, … , xn], entonces:

x12 + x22 + … + xn2 = 1

matrizCuadrada se balancea primero con transformaciones de similaridad hasta que las normas de fila y columna están tan cerca del mismo valor como es posible. La matrizCuadrada se reduce entonces a una forma de Hessenberg superior y los vectores propios se generan o se obtienen por medio de la factorización de Schur.

eigVl(matrizCuadrada)Þlista

Entrega una lista de valores propios de una matrizCuadradareal o compleja.

matrizCuadrada se balancea primero con transformaciones de similaridad hasta que las normas de fila y columna están tan cerca del mismo valor como es posible. La matrizCuadrada se reduce entonces a una forma de Hessenberg superior y los vectores propios se generan o se obtienen por medio de la matriz de Hessenberg superior.

If ExprBooleana1 Then
     Bloque1
ElseIf ExprBooleana2 Then
     Bloque2
©
ElseIf ExprBooleanaN Then
     BloqueN
EndIf
©

Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

euler(Expr, Var, varDep, {Var0, VarMax}, var0Dep, PasoVar [, pasoEuler]) matriz Þ

euler(SistemaDeExpr, Var, ListaDeVarsDep, {Var0, VarMax}, ListaDeVars0Dep, PasoVar [, pasoEuler]) matriz Þ

euler(ListaDeExpr, Var, ListaDeVarsDep, {Var0, VarMax}, ListaDeVars0Dep, PasoVar [, pasoEuler]) matriz Þ

Use el método de Euler para resolver el sistema

con varDep(Var0)=var0Dep en el intervalo [Var0,VarMax]. Entrega una matriz cuya primera fila define los valores del resultado de Var y cuya segunda fila define el valor del primer componente de solución a los valores de Var correspondientes, y así sucesivamente.

Expr es el lado derecho que define la ecuación diferencial ordinaria (EDO).

SistemaDeExpr es el sistema de lados derechos que define el sistema de EDOs (corresponde al orden de variables dependientes en ListaDeVarsDep).

ListaDeExpr es una lista de lados derechos que define el sistema de EDOs (corresponde al orden de variables dependientes en ListaDeVarsDep).

Var es la variable independiente.

ListaDeVarsDep es una lista de variables dependientes.

{Var0, VarMax} es una lista de dos elementos que le dice a la función que se integre de Var0 a VarMax.

ListaDeVars0Dep es una lista de valores iniciales para variables dependientes.

PasoVar es un número distinto de cero de manera que sign(PasoVar) = sign(VarMax‑Var0) y las soluciones se entregan a Var0+i·PasoVar para todos i=0,1,2,… de tal manera que Var0+i·PasoVar está en [var0,VarMax] (puede que no haya un valor de solución en VarMax).

pasoEuler es un entero positivo (predeterminado a 1) que define el número de pasos de Euler entre los valores de resultado. El tamaño del paso real utilizado por el método de Euler es PasoVaràpasoEuler.

Aunque eval() no muestra el resultado, puede ver la cadena de comandos del Concentrador después de ejecutar el comando al inspeccionar cualquiera de las siguientes variables especiales.

iostr.SendAns

iostr.GetAns

iostr.GetStrAns

Nota: Consulte además Get (aquí), GetStr (aquí) y Send (aquí).

exact(Expr1 [, Tolerancia])Þexpresión

exact(Lista1 [, Tolerancia])Þlista

exact(Matriz1 [, Tolerancia])Þmatriz

Usa aritmética de modo Exacto para producir, cuando es posible, el equivalente de número racional del argumento.

Tolerancia especifica la tolerancia para la conversión; la predeterminada es 0 (cero).

Exit

Sale del bloque For, While, o Loop .

Exit no está permitido afuera de las tres estructuras de bucles (For, While, o Loop).

Nota para introducir el ejemplo: Para obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Expr 4exp

Representa la Expr en términos del exponencial natural e. Este es un operador de conversión de despliegue. Se puede usar únicamente al final de la línea de ingreso.

Nota: Usted puede insertar este operador desde el teclado de la computadora al escribir @>exp.

exp(matrizCuadrada1)ÞmatrizCuadrada

Entrega el exponencial de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular e elevado a la potencia de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable. El resultado siempre contiene números de punto flotante.

exp4list(Expr,Var)Þlista

Examina la Expr para las ecuaciones que están separadas por la palabra “or”, y entrega una lista que contiene los lados derechos de las ecuaciones de la forma Var=Expr. Esto le brinda una forma fácil de extraer algunos valores de solución incrustados en los resultados de las funciones solve(), cSolve(), fMin(), y fMax() .

Nota: exp4list() no es necesaria con las funciones zeros() y cZeros() porque entregan una lista de valores de solución en forma directa.

Usted puede insertar esta función desde el teclado al escribir exp@>list(...).

expand(Expr1,[Var]) también distribuye logaritmos y potencias fraccionales independientemente de Var. Para una distribución incrementada de logaritmos y potencias fraccionales, podrían ser necesarias restricciones de desigualdad para garantizar que algunos factores son no negativos.

expand(Expr1, [Var]) también distribuye valores absoluto, sign(), y exponenciales, independientemente de Var.

Nota: Vea también tExpand() para suma de ángulo trigonométrico y expansión de ángulo múltiple.

expr(Cadena)Þexpresión

Entrega la cadena de caracteres contenida en Cadena como una expresión y la ejecuta de inmediato.

ExpReg X, Y [, [Frec] [, Categoría, Incluir]]

Genera la regresión exponencialy = a·(b)xen listas X y Y con frecuencia Frec. Un resumen de resultados se almacena en la variable stat.results (aquí).

Todas las listas deben tener una dimensión igual, excepto por Incluir.

X y Y son listas de variables independientes y dependientes.

Frec es una lista opcional de valores de frecuencia. Cada elemento en Frec especifica la frecuencia de la ocurrencia para cada punto de datos X y Y correspondientes. El valor predeterminado es 1. Todos los elementos deben ser enteros | 0.

Categoría es una lista de códigos de categoría para los datos X y Y correspondientes.

Incluir es una lista de uno o más códigos de categoría. Sólo aquellos elementos de datos cuyo código de categoría está incluido en esta lista están incluidos en el cálculo.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (aquí).