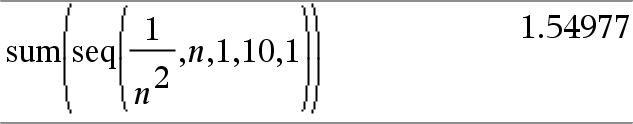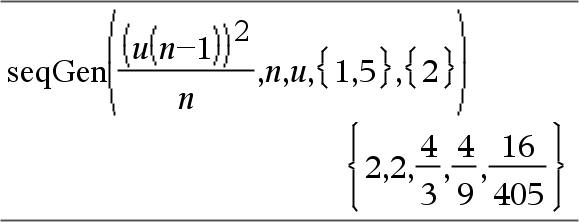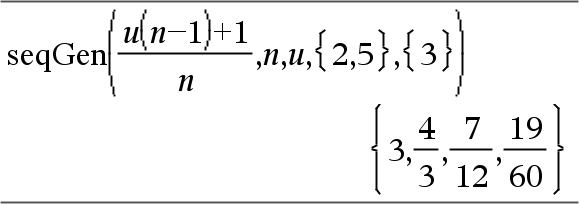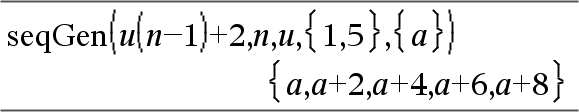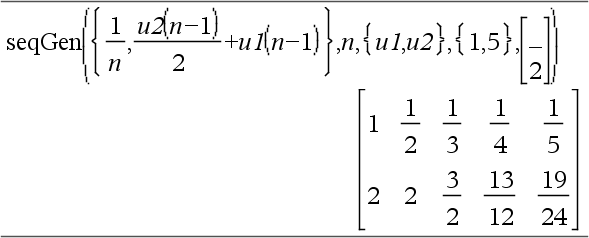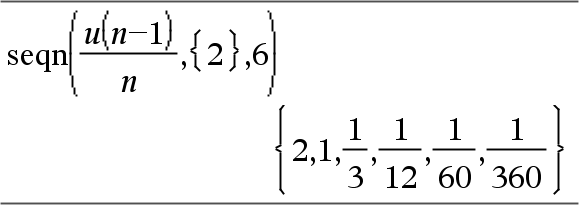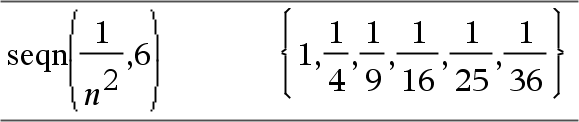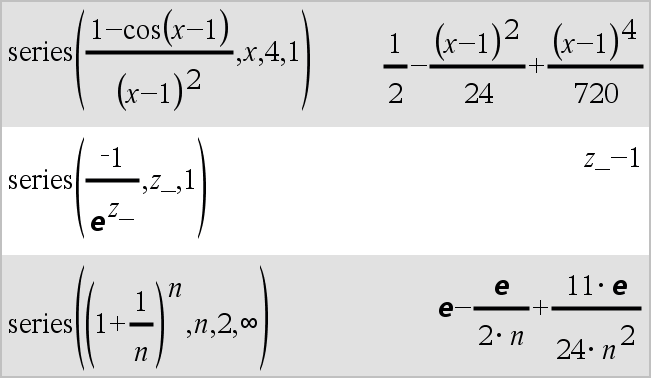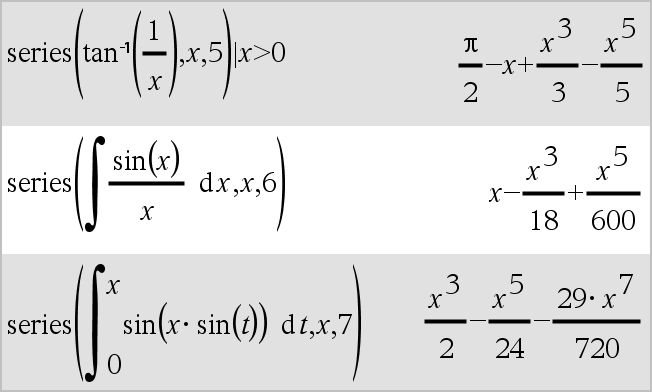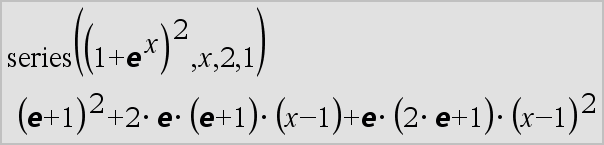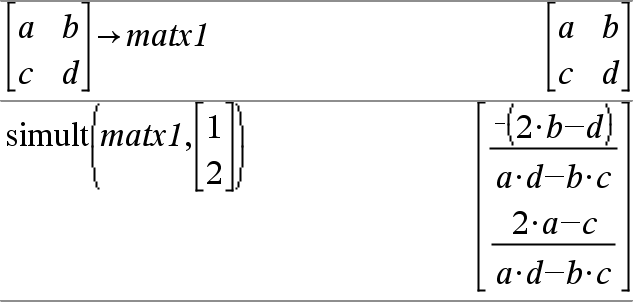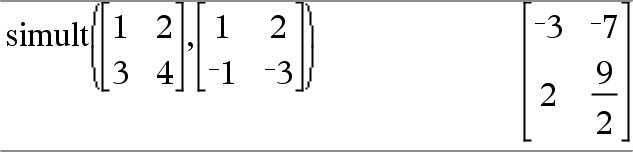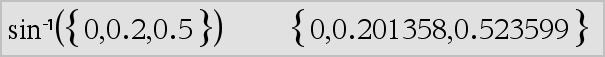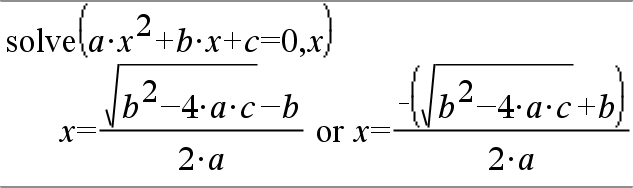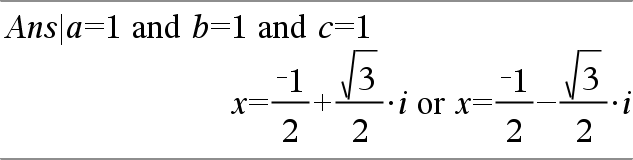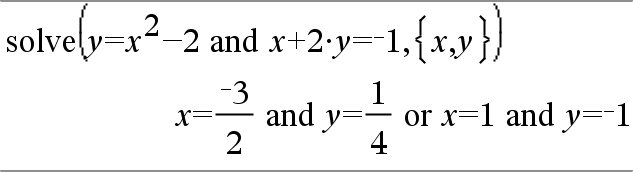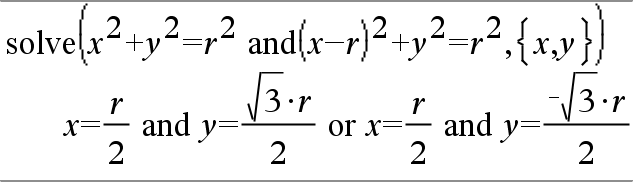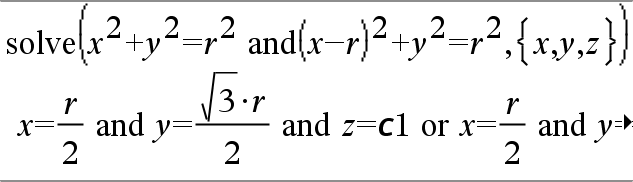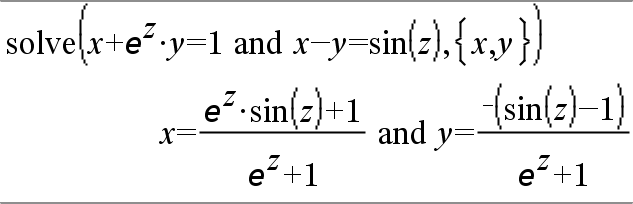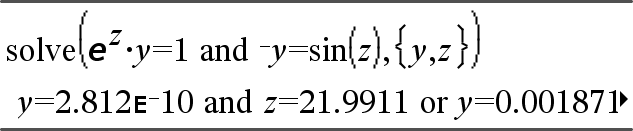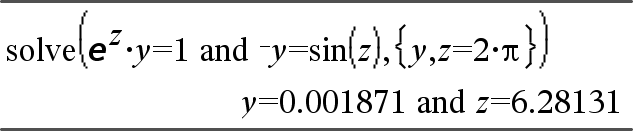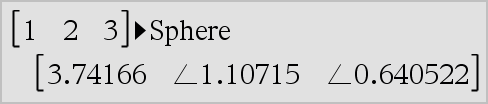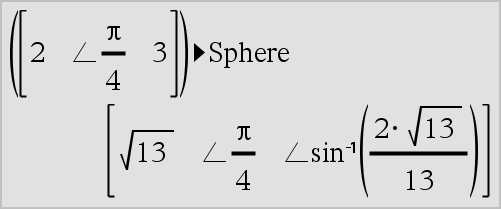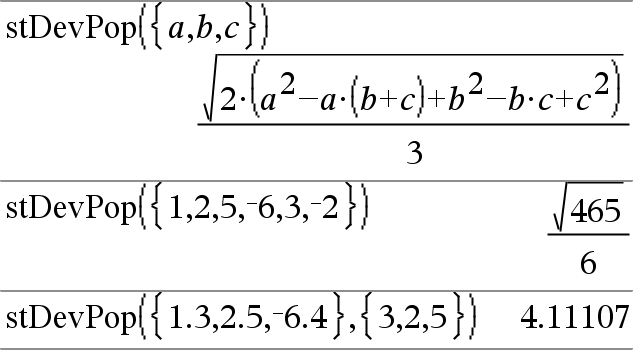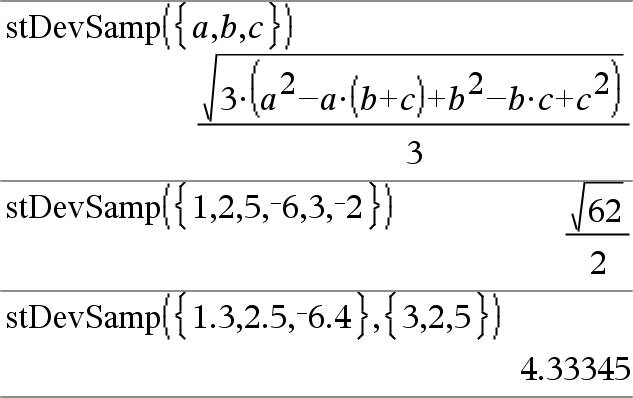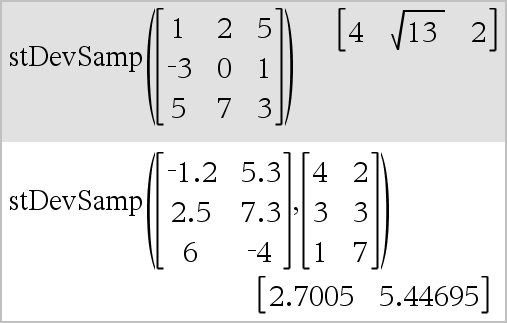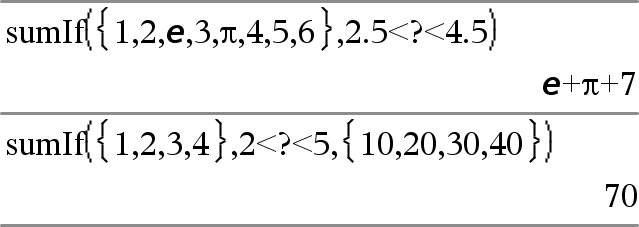|
Tecla µ |
|
|
sec(Expr1) Þ expressão sec(Lista1) Þ lista Devolve a secante de Expr1 ou devolve uma lista com as secantes de todos os elementos em Lista1. Nota: O argumento é interpretado como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Pode utilizar ¡, G ou R para substituir o modo de ângulo temporariamente. |
No modo de ângulo Graus:
|
|
Tecla µ |
|
|
sec/(Expr1) Þ expressão sec/(Lista1) Þ lista Devolve o ângulo cuja secante é Expr1 ou devolve uma lista com as secantes inversas de cada elemento de Lista1. Nota: O resultado é devolvido como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Nota: Pode introduzir esta função através da escrita de arcsec(...) no teclado do computador. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
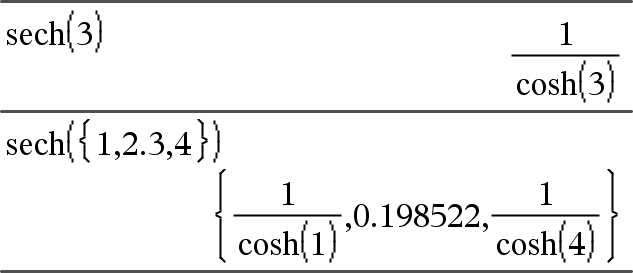
sech(Expr1) Þ expressão sech(Lista1) Þ lista Devolve a secante hiperbólica de Expr1 ou devolve uma lista com as secantes hiperbólicas dos elementos Lista1. |
|
|
Catálogo > |
|
|
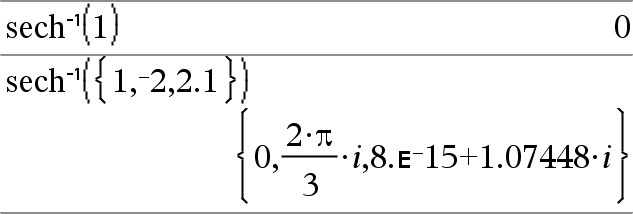
sech/(Expr1) Þ expressão sech/(Lista1) Þ lista Devolve a secante hiperbólica inversa de Expr1 ou devolve uma lista com as secantes hiperbólicas inversas de cada elemento de Lista1. Nota: Pode introduzir esta função através da escrita de arcsech(...) no teclado do computador. |
No modo de ângulo Radianos e Formato complexo rectangular:
|
|
Menu Hub |
|
|
Programar comando: envia um ou mais TI-Innovator™ Hub comandos para um hub conectado. exprOrString tem de ser um TI-Innovator™ Hub comando válido. Tipicamente, exprOrString contém um comando "SET ..." para controlar um dispositivo ou um comando "READ ..." para pedir dados. Os argumentos são enviados sequencialmente para o hub. Nota: pode usar o comando Send dentro de um programa definido pelo utilizador, mas não dentro de uma função. |
Exemplo: ligar o elemento azul do LED RGB incorporado durante 0,5 segundos.
Exemplo: pedir o valor atual do sensor de nível de luz incorporado no hub. Um comando Get recupera o valor e atribui-o à variável lightval.
Exemplo: enviar uma frequência calculada para o altifalante incorporado no hub. Usar a variável especial iostr.SendAns para mostrar o comando do hub com a expressão avaliada.
|
|
Catálogo > |
|
|
seq(Expr, Var, Baixo, Alto [, Passo ]) Þlista Incrementa Var de Baixo até Alto por um incremento de Passo, avalia Expr e apresenta os resultados como uma lista. O conteúdo original de Var ainda está aqui após a conclusão de O valor predefinido para Passo = 1. |
Obs: Para forçar um resultado aproximado, Unidade portátil: Premir / ·.
|
|
Catálogo > |
|
|
Gera uma lista de termos para sequência depVar(Var)=Expr da seguinte forma: Incrementa a variável independente Var de Var0 até VarMax por VarStep, avalia depVar(Var) para os valores correspondentes de Var utilizando a fórmula Expr e ListOfInitTerms e apresenta os resultados como uma lista.
Gera uma matriz de termos de um sistema (ou lista) de sequências ListOfDepVars(Var)=ListOrSystemOfExpr da seguinte forma: Incrementa a variável independente Var de Var0 até VarMax por VarStep, avalia ListOfDepVars(Var) para os valores correspondentes de Var utilizando a fórmula ListOrSystemOfExpr e MatrixOfInitTerms e apresenta os resultados como uma matriz. O conteúdo original de Var está inalterado após a conclusão de O valor predefinido para VarStep = 1. |
Gere o primeiros 5 termos da sequência u(n) = u(n-1)2/2, com u(1)=2 e VarStep=1.
Exemplo no qual Var0=2:
Sistema de duas sequências:
Nota: O Vazio (_) na matriz do termo inicial acima, é utilizado para indicar que o 1º termo para u1(n) é calculado utilizando a fórmula de sucessão u1(n)=1/n. |
|
Catálogo > |
|
|
Gera uma lista de termos para uma sucessão u(n)=Expr(u, n), da seguinte forma: Incrementa n a partir de 1 até nMax por 1, avalia u(n) para os valores correspondentes de n utilizando a fórmula Expr(u, n) e ListOfInitTerms e apresenta os resultados como uma lista.
Gera uma lista de termos para uma sucessão não recorrente u(n)=Expr(n), da seguinte forma: Incrementa n a partir de 1 até nMax por 1, avalia u(n) para os valores correspondentes de n utilizando a fórmula Expr(n) e apresenta os resultados como uma lista. Se nMax estiver em falta, nMax é definido para 2500 Se nMax=0, nMax é definido para 2500 Nota: |
Gere o primeiros 6 termos da sequência u(n) = u(n-1)/2, com u(1)=2.
|
|
Catálogo > |
|
|
série(Expr1, Var, Ordem [, Ponto])Þexpressão série(Expr1, Var, Ordem [, Ponto]) | Var>PontoÞexpressão série(Expr1, Var, Ordem [, Ponto]) Var<PontoÞexpressão
Devolve uma representação da série da potência truncada generalizada de Expr1 expandida sobre Ponto através do grau Ordem. Ordem pode ser qualquer número racional. As potências resultantes de(Var N Ponto) podem incluir expoentes fraccionais e/ou negativos. Os coeficientes destas potências podem incluir logaritmos de (Var N Ponto) e outras funções de Var que são dominadas pelas potências de (Var N Ponto) com o mesmo sinal de expoente. Ponto predefine-se para 0. Ponto pode ser ˆ ou Nˆ, nestes casos, a expansão é efectuada através de grau Ordem em 1/(Var N Ponto). série(...) devolve “série(...)” se não for capaz de determinar uma representação, como para singularidades essenciais, como, por exemplo, sin(1/z) a z=0, eN1/z a z=0, ou ez a z = ˆ ou Nˆ. Se a série ou um das derivadas tiver uma descontinuidade em Ponto, o resultado contém provavelmente subexpressões do sinal(…) ou abs(…) da forma para uma variável de expansão real ou (-1)floor(…ângulo(…)…)para uma variável de expansão complexa, que é uma que termina com “_”. Se quiser utilizar a série apenas para valores num lado de Ponto, adicione o valor adequado de “| Var > Ponto”, “| Var < Ponto”, “| “Var | Ponto”, ou “Var { Ponto” para obter um resultado mais simples. série() pode fornecer aproximações simbólicas para integrais indefinidos para os quais soluções simbólicas podem não ser obtidas. série() distribui-se pelas listas e matrizes do 1º argumento. série() é uma versão generalizada de taylor(). Como ilustrado pelo último exemplo da direita, o fluxo das rotinas do visor do resultado produzido pela série(...) pode reorganizar os termos para que o termo dominante não seja o termo mais à esquerda. Nota: Consulte também dominantTerm(), aqui. |
|
|
Catálogo > |
|
|
setMode(NúmeroInteiroNomeModo, NúmeroInteiroDefinição) Þnúmero inteiro setMode(lista) Þlista de números inteiros Válido apenas numa função ou num programa. setMode(NúmeroInteiroNomeModo, NúmeroInteiroDefinição) define temporariamente o modo NúmeroInteiroNomeModo para a nova definição NúmeroInteiroDefinição e devolve um número inteiro correspondente à definição original desse modo. A alteração é limitada à duração da execução do programa/função. NúmeroInteiroNomeModo especifica que modo quer definir. Tem de ser um dos números inteiros do modo da tabela abaixo. NúmeroInteiroDefinição especifica a nova definição do modo. Tem de ser um dos números inteiros da definição listados abaixo para o modo específico que está a definir. setMode(lista) permite alterar várias definições. lista contém os pares de números inteiros do modo e da lista. setMode(lista) devolve uma lista similar cujos pares de números inteiros representam as definições e os modos originais. Se guardou todas as definições do modo com getMode(0) & var, pode utilizar setMode(var) para restaurar essas definições até sair da função ou do programa. Consulte getMode(), aqui. Nota: As definições do modo actual são passadas para subrotinas. Se uma subrotina alterar uma definição do modo, a alteração do modo perder-se--á quando o controlo voltar à rotina. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
Apresente o valor aproximado de p com a predefinição para Ver dígitos e apresente p com uma definição de Fix2. Certifique-se de que a predefinição é restaurada após a execução do programa.
|
|
Nome do modo |
Número inteiro do modo |
Números inteiros da definição |
|
Ver dígitos |
1 |
1 =Flutuante, 2 =Flutuante1, 3 =Flutuante2, 4 =Flutuante3, 5 =Flutuante4, 6 =Flutuante5, 7 =Flutuante6, 8 =Flutuante7, 9 =Flutuante8, 10 =Flutuante9, 11 =Flutuante10, 12 =Flutuante11, 13 =Flutuante12, 14 =Fixo0, 15 =Fixo1, 16 =Fixo2, 17 =Fixo3, 18 =Fixo4, 19 =Fixo5, 20 =Fixo6, 21 =Fixo7, 22 =Fixo8, 23 =Fixo9, 24 =Fixo10, 25 =Fixo11, 26 =Fixo12 |
|
Ângulo |
2 |
1 =Radianos, 2 =Graus, 3 =Gradianos |
|
Formato exponencial |
3 |
1 =Normal, 2 =Científica, 3 =Engenharia |
|
Real ou Complexo |
4 |
1 =Real, 2 =Rectangular, 3 =Polar |
|
Auto or Aprox. |
5 |
1 =Auto, 2 =Aproximado |
|
Formato vectorial |
6 |
1 =Rectangular, 2 =Cilíndrico, 3 =Esférico |
|
Base |
7 |
1 =Decimal, 2 =Hex, 3 =Binário |
|
Sistema de unidades |
8 |
1 =SI, 2 =Eng/EUA |
|
Catálogo > |
|
|
shift(NúmeroInteiro1 [, #deDeslocações ]) Þnúmero inteiro Desloca os bits num número inteiro binário. Pode introduzir NúmeroInteiro1 em qualquer base numérica; é convertido automaticamente para uma forma binária de 64 bits assinada. Se a magnitude de NúmeroInteiro1 for muito grande para esta forma, uma operação do módulo simétrico coloca-o no intervalo. Para mais informações, consulte 4Base2, aqui. Se #deDeslocações for positivo, a deslocação é para a esquerda. Se #deDeslocações for negativo, a deslocação é para a direita. A predefinição é L1 (deslocar um bit para a direita). Numa deslocação para a direita, o bit mais à direita cai e 0 ou 1 é inserido para corresponder ao bit mais à esquerda. Numa deslocação para a esquerda, o bit mais à esquerda cai e 0 é inserido como o bit mais à direita. Por exemplo, numa deslocação para a direita: Cada bit desloca-se para a direita. 0b0000000000000111101011000011010 Insere 0 se o bit mais à esquerda for 0 ou 1 se o bit mais à esquerda for 1. produz: 0b00000000000000111101011000011010 O resultado aparece de acordo com o modo base. Os zeros à esquerda não aparecem. |
No modo base Bin:
No modo base Hex:
Importante: Para introduzir um número binário ou hexadecimal, utilize sempre o prefixo 0b ou 0h (zero, não a letra O). |
|
shift(Lista1 [, #deDeslocações ]) Þlista Devolve uma cópia de Lista1 deslocada para a direita ou para a esquerda pelos elementos #deDeslocações. Não altere Lista1. Se #deDeslocações for positivo, a deslocação é para a esquerda. Se #deDeslocações for negativo, a deslocação é para a direita. A predefinição é L1 (deslocar um elemento para a direita). Os elementos introduzidos no início ou no fim de lista pela deslocação são definidos para o símbolo “undef”. |
No modo base Dec:
|
|
shift(Cadeia1 [, #deDeslocações ]) Þcadeia Devolve uma cópia de Cadeia1 rodada para a direita ou para a esquerda pelos caracteres #deDeslocações. Não altere Cadeia1. Se #deDeslocações for positivo, a deslocação é para a esquerda. Se #deDeslocações for negativo, a deslocação é para a direita. A predefinição é L1 (deslocar um carácter para a direita). Os caracteres introduzidos no início ou no fim de lista pela deslocação são definidos para um espaço. |
|
|
Catálogo > |
|
|
sign(Expr1) Þexpressão sign(Lista1) Þlista sign(Matriz1) Þmatriz Para Expr1 real ou complexa, devolve Expr1 / abs(Expr1) quando Expr1 ƒ 0. Devolve 1 se Expr1 for positiva. Devolve L1 se Expr1 for negativa. sign(0) devolve „1 se o modo do formato complexo for Real; caso contrário, devolve-se a si próprio. sign(0) representa o círculo no domínio complexo. Para uma lista ou matriz, devolve os sinais de todos os elementos. |
Se o modo do formato complexo for Real:
|
|
Catálogo > |
|||||||
|
simult(MatrizCoef, VectorConst [, Tol ]) Þmatriz Devolve um vector da coluna que contém as soluções para um sistema de equações lineares. Nota: Consulte também MatrizCoef tem de ser uma matriz quadrada que contenha os coeficientes das equações. VectorConst tem de ter o mesmo número de linhas (a mesma dimensão) que MatrizCoef e conter as constantes. Opcionalmente, qualquer elemento da matriz é tratado como zero se o valor absoluto for inferior a Tol. Esta tolerância só é utilizada se a matriz tiver entradas de ponto flutuante e não contiver variáveis simbólicas sem um valor atribuído. Caso contrário, Tol é ignorado.
|
Resolver para x e y: x + 2y = 1 3x + 4y = L1
A solução é x= L3 e y=2.
Resolver: ax + by = 1 cx + dy = 2
|
||||||
|
simult(MatrizCoef, MatrizConst [, Tol ]) Þmatriz Resolve vários sistema de equações lineares, em que cada sistema tem os mesmo coeficientes de equações, mas constantes diferentes. Cada coluna em MatrizConst tem de conter as constantes para um sistema de equações. Cada coluna da matriz resultante contém a solução para o sistema correspondente. |
Resolver: x + 2y = 1 3x + 4y = L1
x + 2y = 2 3x + 4y = L3
Para o primeiro sistema, x= L3 e y=2. Para o segundo sistema, x= L7 e y=9/2. |
|
Catálogo > |
|
|
Expr 4sin Nota: Pode introduzir este operador através da escrita de @>sin no teclado do computador. Representa Expr em função do seno. Este é um operador de conversão. Apenas pode ser utilizado no fim da linha de entrada. 4sin reduz todas as potências de cos(...) módulo 1Nseno(...)^2 para que qualquer polinómio residual de potências de seno(...) tenha expoentes no intervalo [0, 2]. Por conseguinte, o resultado sem cos(...) se e só se cos(...) ocorrer na expressão fornecida apenas em potências pares. Nota: Este operador de conversão não é suportado nos modos de ângulos Graus ou Grados. Antes de o utilizar, certifique-se de que o modo Ângulo está definido para Radianos e que Expr não contém referências explícitas a ângulos em graus ou grados. |
|
|
Tecla µ |
|
|
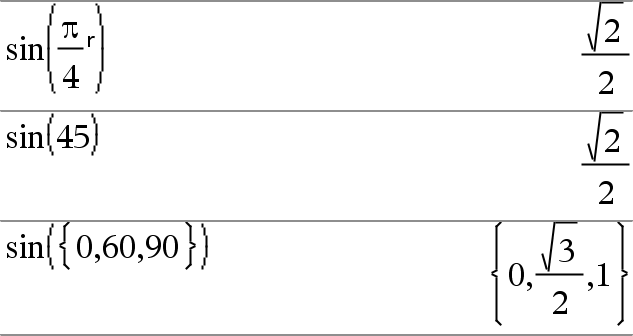
sin(Expr1) Þexpressão sin(Lista1) Þlista
sin(Lista1) devolve uma lista de senos de todos os elementos em Lista1. Nota: O argumento é interpretado como um ângulo expresso em graus, gradianos ou radianos, de acordo com o modo de ângulo actual. Pode utilizar ¡, G ou R para substituir a definição do modo de ângulo temporariamente. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
sin(MatrizQuadrada1) ÞMatrizQuadrada Devolve o seno da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o seno de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
No modo de ângulo Radianos:
|
|
Tecla µ |
|
|
sin/(Expr1) Þexpressão sin/(Lista1) Þlista
sin/(Lista1) devolve uma lista de senos inversos de cada elemento de Lista1. Nota: O resultado é devolvido como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Nota: Pode introduzir esta função através da escrita de arcsin(...) no teclado do computador. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
sin/(MatrizQuadrada1) ÞMatrizQuadrada Devolve o seno inverso da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o seno inverso de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
Nos modos de ângulo Radianos e Formato complexo rectangular:
|
|
Catálogo > |
|
|
sinh(Expr1) Þexpressão sinh(Lista1) Þlista
sinh(Lista1) devolve uma lista dos senos hiperbólicos de cada elemento de Lista1. |
|
|
sinh(MatrizQuadrada1) ÞMatrizQuadrada Devolve o seno hiperbólico da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o seno hiperbólico de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
sinh/(Expr1) Þexpressão sinh/(Lista1) Þlista
sinh/(Lista1) devolve uma lista de senos hiperbólicos inversos de cada elemento de Lista1. Nota: Pode introduzir esta função através da escrita de arcsinh(...) no teclado. |
|
|
sinh/(MatrizQuadrada1) ÞMatrizQuadrada Devolve o seno hiperbólico inverso da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o seno hiperbólico inverso de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
SinReg X, Y [, [Repetições],[ Ponto] [, Categoria, Incluir] ] Calcula a regressão sinusoidal nas listas X e Y. Um resumo dos resultados é guardado na variável stat.results (aqui). Todas as listas têm de ter a mesma dimensão, excepto para Incluir. X e Y são listas de variáveis independentes e dependentes. Iterações é um valor opcional que especifica o número máximo de vezes (de 1 a 16) que uma solução será tentada. Se for omitido, 8 é utilizado. Em geral, valores maiores resultam numa melhor precisão, mas maiores tempos de execução, e vice-versa. Período especifica um período previsto. Se for omitido, a diferença entre os valores em X deve ser igual e por ordem sequencial. Se especificar Período, as diferenças entre os valores x podem ser desiguais. Categoria é uma lista de códigos de categorias para os dados X e Y correspondentes. Incluir é uma lista de um ou mais códigos de categorias. Apenas os itens de dados cujo código de categoria está incluído nesta lista são considerados no cálculo. A saída de SinReg é sempre em radianos, independentemente da definição do modo de ângulo. Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (aqui). |
|
|
Variável de saída |
Descrição |
|
stat.RegEqn |
Equação de regressão: a·sin(bx+c)+d |
|
stat.a, stat.b, stat.c, stat.d |
Parâmetros de regressão |
|
stat.Resid |
Resíduos da regressão |
|
stat.XReg |
Lista de dados na Lista X modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias |
|
stat.YReg |
Lista de dados na Lista Y modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias |
|
stat.FreqReg |
Lista de frequências correspondentes a stat.XReg e stat.YReg |
|
Catálogo > |
|
|
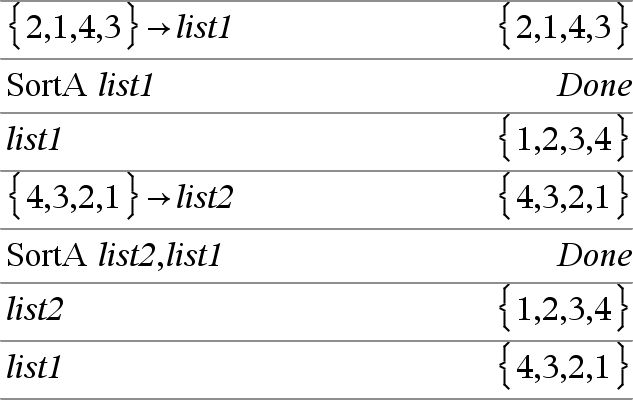
SortA Lista1 [, Lista2 ] [, Lista3 ] ... SortA Vector1 [, Vector2 ] [, Vector3 ] ... Ordena os elementos do primeiro argumento por ordem crescente. Se incluir argumentos adicionais, ordena os elementos para que as novas posições correspondam às novas posições dos elementos no primeiro argumento. Todos os argumentos têm de ter nomes de listas ou vectores. Todos os argumentos têm de ter dimensões iguais. Os elementos (nulos) vazios do primeiro argumento movem-se para a parte inferior. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Catálogo > |
|
|
SortD Lista1 [, Lista2 ] [, Lista3 ] ... SortD Vector1 [, Vector ] [, Vector3 ] ... Idêntico a SortA, excepto que SortD ordena os elementos por ordem decrescente. Os elementos (nulos) vazios do primeiro argumento movem-se para a parte inferior. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Catálogo > |
|
|
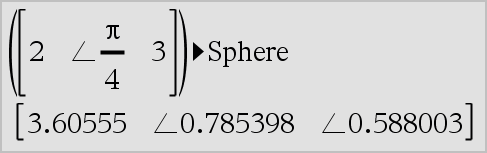
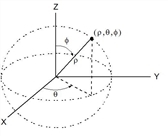
Vector 4Sphere Nota: Pode introduzir esta função através da escrita de @>Sphere no teclado. Apresenta o vector da linha ou coluna em forma esférica [r ±q ±f]. O vector tem de ser de dimensão 3 e pode ser um vector da linha ou coluna. Nota: 4Sphere é uma instrução de formato de visualização, não uma função de conversão. Só pode utilizá-la no fim da linha de entrada. |
Obs: Para forçar um resultado aproximado, Unidade portátil: Premir / ·.
Prima ·
|
|
Catálogo > |
|
|
sqrt(Expr1) Þexpressão sqrt(Lista1) Þlista Devolve a raiz quadrada do argumento. Para uma lista, devolve as raízes quadradas de todos os elementos em Lista1. Nota: Consulte também Modelo de raiz quadrada, aqui. |
|
|
Catálogo > |
|
|
stat.results Apresenta os resultados de um cálculo estatístico. Os resultados aparecem como um conjunto de pares de valores de nomes. Os nomes específicos apresentados estão dependentes do comando ou da função estatística avaliada mais recentemente. Pode copiar um nome ou um valor e colá-lo noutra localização. Nota: Evite definir variáveis que utilizem os mesmos nomes das variáveis utilizadas para análise estatística. Em alguns casos, pode ocorrer uma condição de erro. Os nomes das variáveis utilizados para análise estatística são listados na tabela abaixo. |
|
|
stat.a stat.AdjR² stat.b stat.b0 stat.b1 stat.b2 stat.b3 stat.b4 stat.b5 stat.b6 stat.b7 stat.b8 stat.b9 stat.b10 stat.bList stat.c² stat.c stat.CLower stat.CLowerList stat.CompList stat.CompMatrix stat.CookDist stat.CUpper stat.CUpperList stat.d |
stat.dfDenom stat.dfBlock stat.dfCol stat.dfError stat.dfInteract stat.dfReg stat.dfNumer stat.dfRow stat.DW stat.e stat.ExpMatrix stat.F stat.FBlock stat.Fcol stat.FInteract stat.FreqReg stat.Frow stat.Leverage stat.LowerPred stat.LowerVal stat.m stat.MaxX stat.MaxY stat.ME stat.MedianX |
stat.MedianY stat.MEPred stat.MinX stat.MinY stat.MS stat.MSBlock stat.MSCol stat.MSError stat.MSInteract stat.MSReg stat.MSRow stat.n stat.Ç stat.Ç1 stat.Ç2 stat.ÇDiff stat.PList stat.PVal stat.PValBlock stat.PValCol stat.PValInteract stat.PValRow stat.Q1X stat.Q1Y |
stat.Q3X stat.Q3Y stat.r stat.r² stat.RegEqn stat.Resid stat.ResidTrans stat.sx stat.sy stat.sx1 stat.sx2 stat.Gx stat.Gx² stat.Gxy stat.Gy stat.Gy² stat.s stat.SE stat.SEList stat.SEPred stat.sResid stat.SEslope stat.sp stat.SS |
stat.SSBlock stat.SSCol stat.SSX stat.SSY stat.SSError stat.SSInteract stat.SSReg stat.SSRow stat.tList stat.UpperPred stat.UpperVal stat.v stat.v1 stat.v2 stat.vDiff stat.vList stat.XReg stat.XVal stat.XValList stat.w stat.y stat.yList stat.YReg |
|
Nota: Sempre que a aplicação Listas e Folha de Cálculo calcula parâmetros estatísticos, copia as variáveis do grupo “stat.” para um grupo “stat#.”, em que # é um número que é incrementado automaticamente. Isto permite manter os resultados anteriores durante a execução de vários cálculos. |
|
Catálogo > |
|
|
stat.values Apresenta uma matriz dos valores calculados para o comando ou a função estatística avaliada mais recentemente. Ao contrário de stat.results, stat.valu omite os nomes associados aos valores. Pode copiar um valor e colá-lo noutras localizações. |
Consulte o exemplo de stat.results. |
|
Catálogo > |
|
|
stDevPop(Lista [, ListFreq ])Þ Devolve o desvio padrão da população dos elementos em Lista. Cada elemento de ListFreq conta o número de ocorrências consecutivas do elemento correspondente em Lista. Nota: Lista tem de ter pelo menos dois elementos. Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
Nos modos auto e de ângulo Radianos:
|
|
stDevPop(Matriz1 [, MatrizFreq ]) Þmatriz Devolve um vector da linha dos desvios padrão da população das colunas em Matriz1. Cada elemento de ListaFreq conta o número de ocorrências consecutivas do elemento correspondente em Matriz1. Nota: Matriz1 tem de ter pelo menos duas linhas. Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Catálogo > |
|
|
stDevSamp(Lista [, ListaFreq ]) Þexpressão Devolve o desvio padrão da amostra dos elementos em Lista. Cada elemento de ListFreq conta o número de ocorrências consecutivas do elemento correspondente em Lista. Nota: Lista tem de ter pelo menos dois elementos. Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
stDevSamp(Matriz1 [, MatrizFreq ]) Þmatriz Devolve um vector da coluna dos desvios padrão da amostra das colunas em Matriz1. Cada elemento de ListaFreq conta o número de ocorrências consecutivas do elemento correspondente em Matriz1. Nota: Matriz1 tem de ter pelo menos duas linhas. Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Catálogo > |
|
|
Stop Programar comando: Termina o programa. Stop não é permitido em funções. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
|
|
Consulte & (guardar), aqui. |
|
|
|
|
|
Catálogo > |
|
|
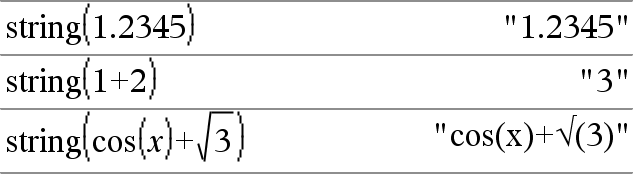
strin g(Expr) Þcadeia Simplifica Expr e devolve o resultado como uma cadeia de caracteres. |
|
|
Catálogo > |
|
|
subMa t(Matriz1 [, LinhaInicial ] [, ColInicial ] [, LinhaFinal ] [, ColFinal ]) Þmatrix Devolve a submatriz especificada de Matriz1. Predefinições: LinhaInicial =1, ColInicial =1, LinhaFinal =última linha, ColFinal =última coluna. |
|
|
Consulte G(), aqui. |
|
|
|
|
|
Catálogo > |
|
|
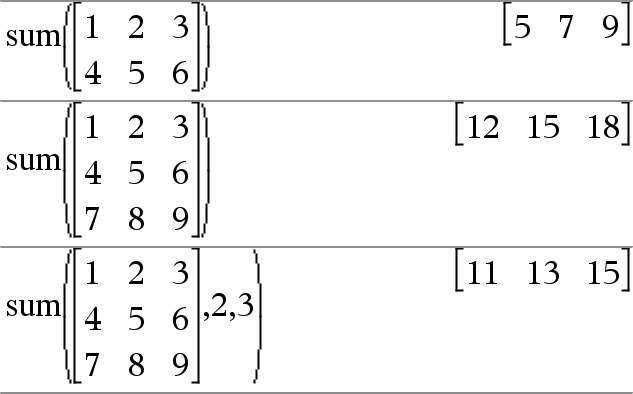
sum(Lista [, Início [, Fim ]]) Þexpressão Devolve a soma dos elementos em Lista. Início e Fim são opcionais. Especificam um intervalo de elementos. Qualquer argumento vazio produz um resultado vazio. Os elementos (nulos) vazios da Lista são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
sum(Matrix1 [, Início [, Fim ]]) Þmatriz Devolve um vector da linha com as somas dos elementos nas colunas em Matriz1. Início e Fim são opcionais. Especificam um intervalo de linhas. Qualquer argumento vazio produz um resultado vazio. Os elementos (nulos) vazios da Matriz1 são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Catálogo > |
|||||||
|
sumIf(Lista, Critérios [, ListaDeSomas ]) Þvalor Devolve a soma acumulada de todos os elementos em Lista que satisfazem os Critérios especificados. Opcionalmente, pode especificar uma lista alternativa, ListaDeSomas, para fornecer os elementos a acumular. Lista pode ser uma expressão, lista ou matriz. ListaDeSomas, se especificada, tem de ter as mesmas dimensões que Lista. Critérios podem ser:
Quando um elementos da Lista cumprir os Critérios, o elemento é adicionado à soma acumulada. Se incluir ListaDeSomas, o elemento correspondente de ListaDeSomas é adicionado à soma. Na aplicação Listas e Folha de cálculo, pode utilizar um intervalo de células no lugar de Lista e de ListaDeSomas. Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. Nota: Consulte também countIf(), aqui. |
|
|
Consulte G(), aqui. |
|
|
|
|
|
Catálogo > |
|
|
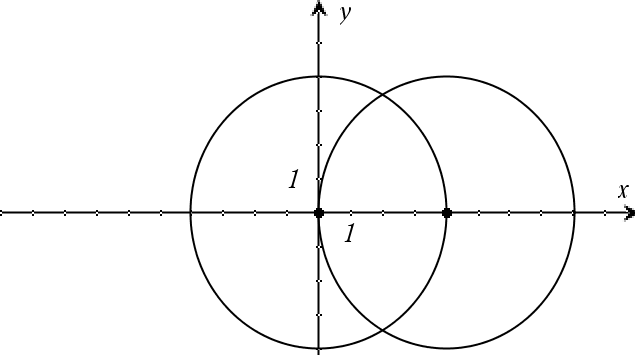
system(Equ1 [, Equ2 [, Equ3 [, ...]]]) system(Expr1 [, Expr2 [, Expr3 [, ...]]]) Devolve um sistema de equações formatado como uma lista. Pode também criar um sistema com um modelo.
|
|








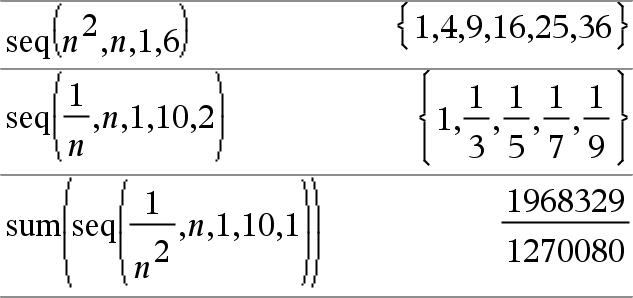
 .
.