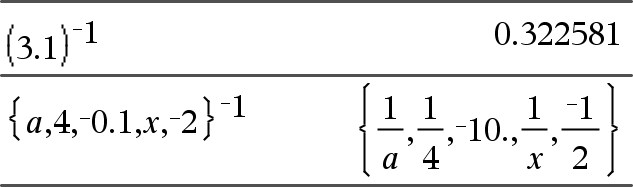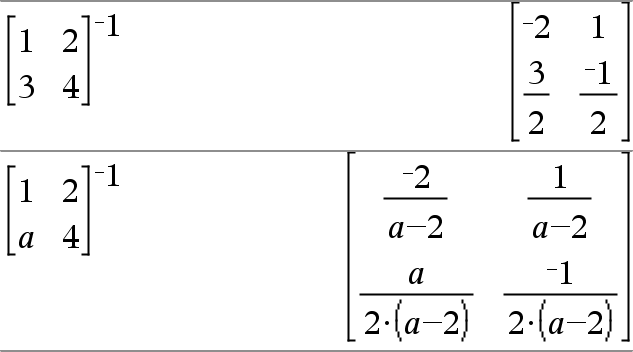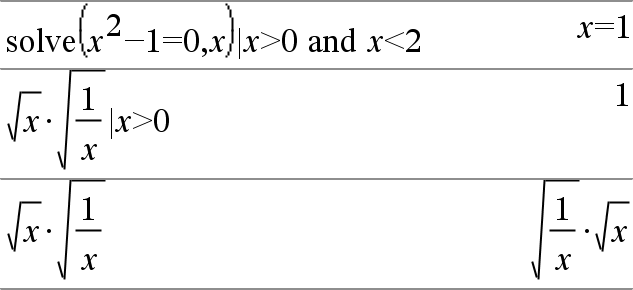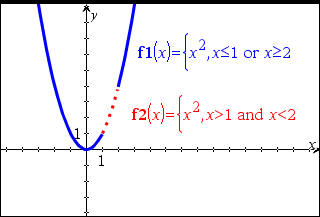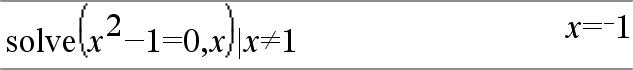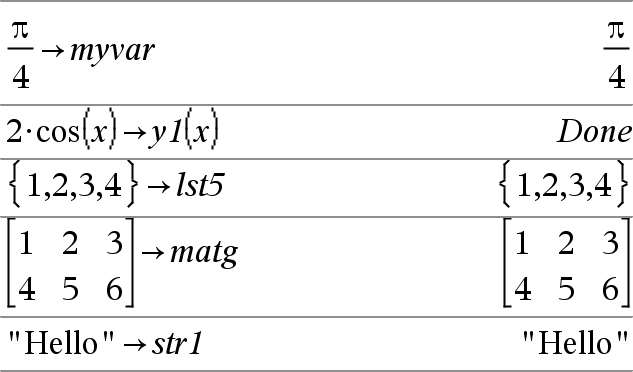|
Tecla + |
|
|
Devolve a soma dos dois argumentos. |
|
|
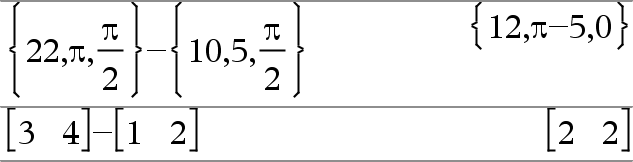
Lista1 + Lista2 Þlista Matriz1 + Matriz2 Þmatriz Devolve uma lista (ou matriz) com as somas dos elementos correspondentes em Lista1 e Lista2 (ou Matriz1 e Matriz2). As dimensões dos argumentos têm de ser iguais. |
|
|
Lista1 + Expr Þlista Devolve uma lista com as somas de Expr e de cada elemento em Lista1. |
|
|
Matriz1 + Expr Þmatriz Devolve uma matriz com Expr adicionada a cada elemento na diagonal de Matriz1. Matriz1 tem de ser quadrada. Nota: Utilize .+ (ponto mais) para adicionar uma expressão a cada elemento. |
|
|
Tecla - |
|
|
Devolve Expr1 menos Expr2. |
|
|
Lista1 N Lista2 Þlista Matriz1 N Matriz2 Þmatriz Subtrai cada elmento em Lista2 (ou Matriz2) do elemento correspondente em Lista1 (ou Matriz1) e devolve os resultados. As dimensões dos argumentos têm de ser iguais. |
|
|
Lista1 N Expr Þlista Subtrai cada elemento de Lista1 de Expr ou subtrai Expr de cada elemento de Lista1 e devolve uma lista de resultados. |
|
|
Matriz1 N Expr Þmatriz Expr N Matriz1 devolve uma matriz de Expr vezes a matriz de identidade menos Matriz1. Matriz1 tem de ser quadrada. Matriz1 N Expr devolve uma matriz de Expr vezes a matriz de identidade subtraída de Matriz1. Matriz1 tem de ser quadrada. Nota: Utilize .N (ponto menos) para subtrair uma expressão de cada elemento. |
|
|
Tecla r |
|
|
Devolve o produto dos dois argumentos. |
|
|
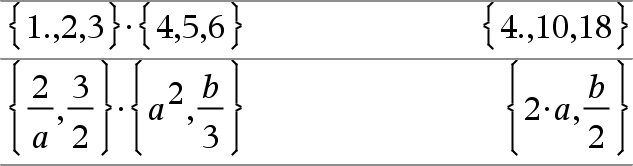
Lista1 · Lista2 Þlista Devolve uma lista com os produtos dos elementos correspondentes em Lista1 e Lista2. As dimensões das listas têm de ser iguais. |
|
|
Matriz1 · Matriz2 Þmatriz Devolve o produto da matriz de Matriz1 e Matriz2. O número de colunas em Matriz1 tem de ser igual ao número de linhas em Matriz2. |
|
|
Lista1 · Expr Þlista Devolve uma lista com os produtos de Expr e de cada elemento em Lista1. |
|
|
Matriz1 · Expr Þmatriz Devolve uma matriz com os produtos de Expr e de cada elemento em Matriz1. Nota: Utilize .· (ponto multiplicar) para multiplicar uma expressão por cada elemento. |
|
|
Tecla p |
|
|
Devolve o quociente de Expr1 dividido pela Expr2. Nota: Consulte também Modelo da fracção, aqui. |
|
|
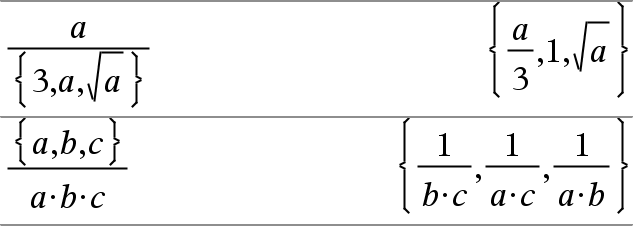
Lista1 à Lista2 Þlista Devolve uma lista com os quocientes de Lista1 divididos pela Lista2. As dimensões das listas têm de ser iguais. |
|
|
Lista1 à Expr Þ lista Devolve uma lista com os quocientes de Expr divididos pela Lista1 ou de Lista1 divididos pela Expr. |
|
|
Devolve uma matriz com os quocientes de Matriz1 à Expr. Nota: Utilize . / (ponto dividir) para dividir uma expressão por cada elemento. |
|
|
Tecla l |
|
|
Lista1 ^ Lista2 Þ lista Devolve o primeiro argumento elevado à potência do segundo argumento. Nota: Consulte também Modelo do expoente, aqui. Para uma lista, devolve os elementos em Lista1 elevados à potência dos elementos correspondentes em Lista2. No domínio real, as potências fraccionárias que tenham expoentes simplificados com denominadores ímpares utilizam a derivação real versus a derivação principal para o modo complexo. |
|
|
Devolve Expr elevada à potência dos elementos em Lista1. |
|
|
Devolve os elementos em Lista1 elevados à potência de Expr. |
|
|
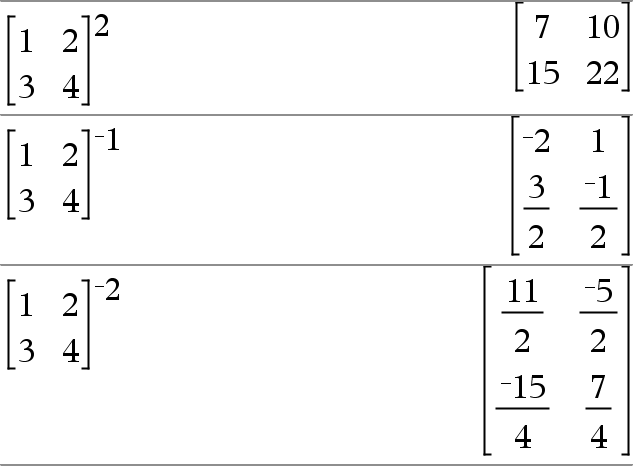
MatrizQuadrada1 ^ número inteiro Þ matriz Devolve MatrizQuadrada1 elevada à potência do número inteiro. MatrizQuadrada1 tem de ser uma matriz quadrada. Se número inteiro = L1, calcula a matriz inversa. Se número inteiro < L1, calcula a matriz inversa para uma potência positiva adequada. |
|
|
Tecla q |
|
|
Devolve o quadrado do argumento. Lista1 2 Þ lista Devolve uma lista com os quadrados dos elementos em Lista1. MatrizQuadrada1 2 Þ matriz Devolve a matriz quadrada de MatrizQuadrada1. Isto não é o mesmo que calcular o quadrado de cada elemento. Utilize .^2 para calcular o quadrado de cada elemento. |
|
|
Teclas ^+ |
|
|
Matriz1 .+ Matriz2 Þ matriz
Matriz1 .+ Matriz2 devolve uma matriz que é a soma de cada par dos elementos correspondentes em Matriz1 e Matriz2.
|
|
|
Teclas ^- |
|
|
Matriz1 .N Matriz2 Þ matriz Matriz1 .NMatriz2 devolve uma matriz que é a diferença entre cada par de elementos correspondentes em Matriz1 e Matriz2.
|
|
|
Teclas ^r |
|
|
Matriz1 .· Matriz2 Þ matriz
Matriz1 .· Matriz2 devolve uma matriz que é o produto de cada par dos elementos correspondentes em Matriz1 e Matriz2.
|
|
|
Teclas ^p |
|
|
Matriz1 . / Matriz2 Þ matriz Matriz1 ./ Matriz2 devolve uma matriz que é o quociente de cada par de elementos correspondente em Matriz1 e Matriz2.
|
|
|
Teclas ^l |
|
|
Matriz1 .^ Matriz2 Þ matriz Matriz1 .^ Matriz2 devolve uma matriz em que cada elemento em Matriz2 é o expoente para o elemento correspondente em Matriz1.
|
|
|
Tecla v |
|
|
LLista1 Þ lista LMatriz1 Þ matriz Devolve a negação do argumento. Para uma lista ou matriz, devolve todos os elementos negados. Se o argumento for um número inteiro binário ou hexadecimal, a negação dá o complemento de dois. |
No modo base Bin: Importante: Zero, não a letra O
Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. |
|
Teclas /k |
|
|
Lista1 % Þ lista Matriz1 % Þ matriz Devolve Para uma lista ou matriz, devolve uma lista ou matriz com cada elemento dividido por 100. |
Obs: Para forçar um resultado aproximado, Unidade portátil: Premir / ·.
|
|
Tecla = |
|
|
Expr1 = Expr2 ÞExpressão booleana Lista1 = Lista2 Þ Lista booleana Matriz1 = Matriz2 Þ Matriz booleana Devolve verdadeiro se Expr1 for determinada para ser igual a Expr2. Devolve falso se Expr1 for determinada para ser diferente a Expr2. Outra coisa qualquer devolve uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
Exemplo de função que utiliza os símbolos de teste matemático: =, ƒ, <, {, >, |
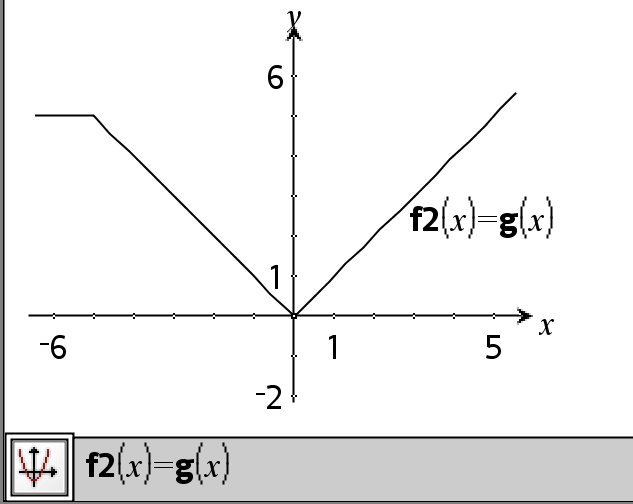
Resultado do gráfico g(x)
|
|
Teclas /= |
|
|
Expr1 ƒ Expr2 Þ Expressão booleana Lista1 ƒ Lista2 Þ Lista booleana Matriz1 ƒ Matriz2 Þ Matriz booleana Devolve verdadeiro se Expr1 for determinada para ser diferente a Expr2. Devolve falso se Expr1 for determinada para ser igual a Expr2. Outra coisa qualquer devolve uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. Nota: Pode introduzir este operador através da escrita de /= no teclado. |
Consulte exemplo “=” (igual). |
|
Teclas /= |
|
|
Expr1 < Expr2 Þ Expressão booleana Lista1 < Lista2 Þ Lista booleana Matriz1 < Matriz2 Þ Matriz booleana Devolve verdadeiro se Expr1 for determinada para ser menor que Expr2. Devolve falso se Expr1 for determinada para ser igual ou maior que Expr2. Outra coisa qualquer devolve uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. |
Consulte exemplo “=” (igual). |
|
Teclas /= |
|
|
Expr1 { Expr2 Þ Expressão booleana Lista1 { Lista2 Þ Lista booleana Matriz1 { Matriz2 Þ Matriz booleana Devolve verdadeiro se Expr1 for determinada para igual ou menor que Expr2. Devolve falso se Expr1 for determinada para ser maior que Expr2. Outra coisa qualquer devolve uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. Nota: Pode introduzir este operador através da escrita de <= no teclado |
Consulte exemplo “=” (igual). |
|
Teclas /= |
|
|
Expr1 > Expr2 Þ Expressão booleana Lista1 > Lista2 Þ Lista booleana Matriz1 > Matriz2 Þ Matriz booleana Devolve verdadeiro se Expr1 for determinada para ser maior que Expr2. Devolve falso se Expr1 for determinada para ser igual ou menor que Expr2. Outra coisa qualquer devolve uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. |
Consulte exemplo “=” (igual). |
|
Teclas /= |
|
|
Expr1 | Expr2 Þ Expressão booleana Lista1 | Lista2 Þ Lista booleana Matriz1 | Matriz2 Þ Matriz booleana Devolve verdadeiro se Expr1 for determinada para ser igual ou maior que Expr2. Devolve falso se Expr1 for determinada para ser menor que Expr2. Outra coisa qualquer devolve uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. Nota: Pode introduzir este operador através da escrita de >= no teclado. |
Consulte exemplo “=” (igual). |
|
Teclas /= |
|
|
ExprBooleana1 Þ ExprBooleana2 devolve expressão booleana ListaBooleana1 Þ ListaBooleana2 devolve lista booleana MatrizBooleana1 Þ MatrizBooleana2 devolve matriz booleana NúmeroInteiro1 Þ NúmeroInteiro2 devolve número inteiro
Avalia a expressão not <argumento1> or <argumento2> e devolve falso, verdadeiro ou uma forma simplificada da equação. Para listas e matrizes, devolve comparações elemento por elemento. Nota: Pode introduzir este operador ao escrever => com o teclado |
|
|
Teclas /= |
|
|
ExprBooleana1 Û ExprBooleana2 devolve expressão booleana ListaBooleana1 Û ListaBooleana2 devolve lista booleana MatrizBooleana1 Û MatrizBooleana2 devolve matriz booleana NúmeroInteiro1 Û NúmeroInteiro2 devolve número inteiro
Devolve a negação de uma operação booleana Para listas e matrizes, devolve comparações elemento por elemento. Nota: Pode introduzir este operador ao escrever <=> com o teclado |
|
|
Tecla º |
|
|
Lista1! Þ lista Matriz1! Þ matriz Devolve o factorial do argumento. Para uma lista ou matriz, devolve uma lista ou matriz de factoriais dos elementos. |
|
|
Teclas /k |
|
|
Cadeia1 & Cadeia2 Þ cadeia Devolve uma cadeia de texto que é Cadeia2 acrescentada a Cadeia1. |
|
|
Catálogo > |
||||||||||
|
d(Expr1, Var[, Ordem])Þexpressão d(Lista1, Var[, Ordem])Þlista d(Matriz1, Var[, Ordem])Þmatriz Devolve a primeira derivada do primeiro argumento em relação à variável Var. Ordem, se incluída, tem de ser um número inteiro. Se a ordem for inferior a zero, o resultado será uma antiderivada. Nota: Pode introduzir isto através da escrita de
|
|
|
Catálogo > |
|
|
‰(Expr1, Var[, Inferior, Superior]) Þ expressão ‰(Expr1, Var[, Constante]) Þ expressão Devolve o integral de Expr1 em relação à variável Var de Inferior a Superior. Nota: Consulte também o modelo de integral definido ou indefinido, aqui. Nota: Pode introduzir esta função através do teclado, escrevendo integral(...). |
|
|
Devolve uma antiderivada se Inferior e Superior forem omitidos. Uma constante simbólica de integração é omitida, excepto se fornecer o argumento Constante. |
|
|
As primitivas igualmente válidas podem diferir por uma constante numérica. Essa constante pode estar disfarçada—em especial, quando uma primitiva contiver logaritmos ou funções trigonométricas inversas. Além disso, as expressões constantes piecewise são por vezes adicionadas para validar uma primitiva sobre um intervalo maior que a fórmula usual. |
|
|
‰() devolve-se por partes de Expr1 que não pode ser determinada como uma combinação finita explícita dos operadores e das funções integrados. Quando fornecer Inferior e Superior, é efectuada uma tentativa para localizar qualquer descontinuidade ou derivada descontínua no intervalo Inferior < Var < Superior e subdividir o intervalo nesses locais. |
|
|
Para a definição Auto do modo Auto ou Aproximado, a integração numérica é utilizada onde aplicável quando não for possível determinar uma primitiva ou um limite. |
|
|
Para a definição Aproximado, a integração numérica é tentada primeiro, se aplicável. As primitivas são procuradas apenas onde essa integração numérica não seja aplicável ou falhar. |
Obs: Para forçar um resultado aproximado, Unidade portátil: Premir / ·.
|
|
‰() pode ser aninhada para fazer vários integrais. Os limites da integração podem depender das variáveis de integração fora dos limites. Nota: Consulte também nInt(), aqui. |
|
|
Teclas /q |
|
|
‡(Lista1) Þlista Devolve a raiz quadrada do argumento. Para uma lista, devolve as raízes quadradas de todos os elementos em Lista1. Nota: Pode introduzir esta função através da escrita de sqrt(...) no teclado Nota: Consulte também Modelo de raiz quadrada, aqui. |
|
|
Catálogo > |
|
|
P (Expr1, Var, Baixo, Alto) Þexpressão Nota: Pode introduzir esta função através da escrita de prodSeq(...) no teclado. Avalia Expr1 para cada valor de Var de Baixo a Alto e devolve o produto dos resultados. Nota: Consulte também Modelo do produto ( P) , aqui. |
|
|
P (Expr1, Var, Baixo, Baixo N1)Þ1 P (Expr1, Var, Baixo, Alto) Þ1/ P (Expr1, Var, Alto+1, Baixo N1) se Alto < Baixo N1
As fórmulas do produto utilizadas derivam da seguinte referência: Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catálogo > |
|
|
G(Expr1, Var, Baixo, Alto) Þexpressão Nota: Pode introduzir esta função através da escrita de sumSeq(...) no teclado. Avalia Expr1 para cada valor de Var de Baixo a Alto e devolve a soma dos resultados. Nota: Consulte também Modelo da soma, aqui. |
|
|
G(Expr1, Var, Baixo, Baixo N1)Þ0 G(Expr1, Var, Baixo, Alto) ÞLG(Expr1, Var, Alto+1, Baixo N1) se Alto < Baixo N1
As fórmulas da soma utilizadas derivam da seguinte referência : Ronald L. Graham, Donald E. Knuth, and Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Catálogo > |
||||||||||
|
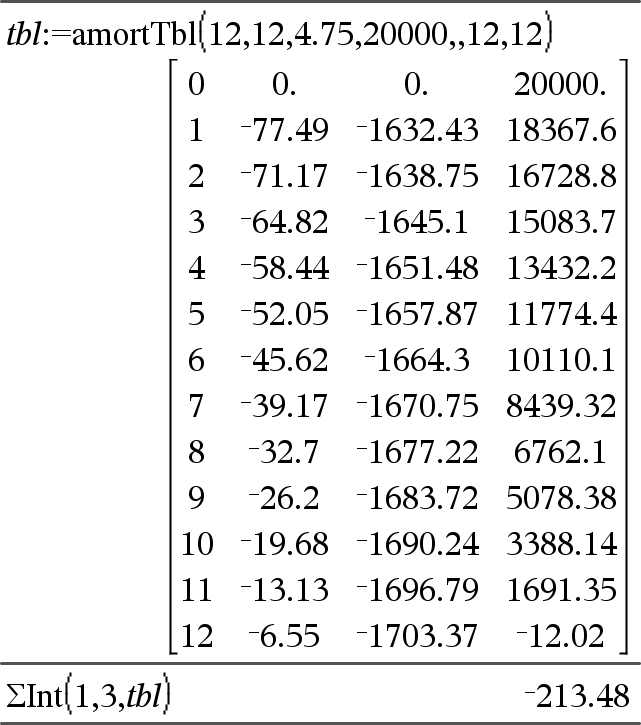
GInt(NPmt1, NPmt2, N, I, PV, [ Pmt ], [ FV ], [ PpY ], [ CpY ], [ PmtAt ], [ ValorArredondado ]) Þvalor GInt(NPmt1, NPmt2, TabelaDeDepreciação) Þvalor Função de amortização que calcula a soma do juro durante um intervalo especificado de pagamentos. NPmt1 e NPmt2 definem os limites iniciais e finais do intervalo de pagamentos. N, I, PV, Pmt, FV, PpY, CpY e PmtAt são descritos na tabela de argumentos TVM, aqui.
ValorArredondado especifica o número de casas decimais para arredondamento. Predefinição=2. GInt(NPmt1,NPmt2, TabelaDeDepreciação) calcula a soma dos juros com base na tabela de amortização TabelaDeDepreciação. O argumento TabelaDeDepreciação tem de ser uma matriz na forma descrita em amortTbl(), aqui. Nota: Consulte também GPrn(), abaixo, e Bal(), aqui. |
|
|
Catálogo > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [ Pmt ], [ FV ], [ PpY ], [ CpY ], [ PmtAt ], [ ValorArredondado ]) Þvalor GPrn(NPmt1, NPmt2, TabelaDeDepreciação) Þvalor Função de amortização que calcula a soma do capital durante um intervalo especificado de pagamentos. NPmt1 e NPmt2 definem os limites iniciais e finais do intervalo de pagamentos. N, I, PV, Pmt, FV, PpY, CpY e PmtAt são descritos na tabela de argumentos TVM, aqui.
ValorArredondado especifica o número de casas decimais para arredondamento. Predefinição=2. GPrn(NPmt1,NPmt2, TabelaDeDepreciação) calcula a soma do capital pago com base na tabela de amortização TabelaDeDepreciação. O argumento TabelaDeDepreciação tem de ser uma matriz na forma descrita em amortTbl(), aqui. Nota: Consulte também GInt(), acima, e Bal(), aqui. |
|
|
Teclas /k |
|
|
# CadeiaDeNomeDaVar Refere-se à variável cujo nome é CadeiaDeNomeDaVar. Permite utilizar cadeias para criar nomes das variáveis a partir de uma função. |
Cria ou refere-se à variável xyz.
Devolve o valor da variável (r) cujo nome é guardado na variável s1. |
|
Tecla i |
|
|
mantissa E expoente Introduz um número em notação científica. O número é interpretado como mantissa × 10 expoente. Sugestão: Se quiser introduzir uma potência de 10 sem resultar num resultado de valor decimal, utilize 10^ número inteiro. Nota: Pode introduzir este operador através da escrita de @E no teclado do computador. por exemplo, escreva 2.3@E4 para introduzir 2.3E4. |
|
|
Tecla 1 |
|
|
Lista1g Þlista Matriz1g Þmatriz Esta função fornece uma forma para especificar um ângulo de gradianos enquanto está no modo Graus ou Radianos. No modo de ângulo Radianos, multiplica Expr1 por p/200. No modo de ângulo Graus, multiplica Expr1 por g/100. No modo Gradianos, devolve Expr1 inalterada. Nota: Pode introduzir este símbolo através da escrita de @g no teclado do computador. |
No modo Graus, Gradianos ou Radianos:
|
|
Tecla 1 |
|
|
Lista1RÞlista Matriz1RÞmatriz Esta função fornece uma forma para especificar um ângulo de radianos enquanto está no modo Graus ou Gradianos. No modo de ângulo Graus, multiplica o argumento por 180/ p. No modo de ângulo Radianos, devolve o argumento inalterado. No modo Gradianos, multiplica o argumento por 200/ p. Sugestão: Utilize R se quiser impor os radianos numa definição da função, independentemente do modo que prevalece quando a função é utilizada. Nota: Pode introduzir este símbolo através da escrita de @r no teclado. |
No modo de ângulo Graus, Gradianos ou Radianos:
|
|
Tecla 1 |
|
|
Lista1 ¡Þlista Matriz1 ¡Þmatriz Esta função fornece uma forma para especificar um ângulo expresso em graus enquanto está no modo Radianos ou Radianos. No modo de ângulo Radianos, multiplica o argumento por p/180. No modo de ângulo Graus, devolve o argumento inalterado. No modo de ângulo Gradianos, multiplica o argumento por 10/9. Nota: Pode introduzir este símbolo através da escrita de @d no teclado do computador. |
No modo de ângulo Graus, Gradianos ou Radianos:
No modo de ângulo Radianos: Obs: Para forçar um resultado aproximado, Unidade portátil: Premir / ·.
|
|
Teclas /k |
|||||||
|
gg ¡mm ' ss.ss '' Þexpressão gg Um número positivo ou negativo mm Um número não negativo ss.ss Um número não negativo Devolve gg +(mm /60)+(ss.ss /3600). Este formato de entrada base ‑60 permite:
Nota: Introduza dois apóstrofos a seguir ss.ss (''), não um símbolo de aspas ("). |
No modo de ângulo Graus:
|
|
Teclas /k |
|
|
[ Raio, ±q_Ângulo ] Þvector (entrada polar) [ Raio, ±q_Ângulo, Z_Coordenada ] Þvector (entrada cilíndrica) [ Raio, ±q_Ângulo, ±q_Ângulo ] Þvector (entrada esférica) Devolve coordenadas como um vector dependendo da definição do modo Formato do vector: rectangular, cilíndrico ou esférico. Nota: Pode introduzir este símbolo através da escrita de @< no teclado do computador. |
No modo Radianos e formato do vector definido para: rectangular
cilíndrico
esférico
|
|
(Magnitude ± Ângulo) ÞValorComplexo (entrada polar) Introduz um valor complexo em forma polar (r ±q). O Ângulo é interpretado de acordo com a definição do modo Ângulo actual. |
No modo de ângulo Radianos e Formato complexo rectangular:
Obs: Para forçar um resultado aproximado, Unidade portátil: Premir / ·.
|
|
Tecla º |
|
|
variável ' variável '' Introduz um símbolo de plica numa equação diferencial. Um símbolo de plica indica uma equação diferencial de 1ª ordem, dois símbolos de números primos indicam uma 2ª ordem, etc. |
|
|
Consulte “Elementos (nulos) vazios” , aqui. |
|
|
|
|
|
Teclas /_ |
|
|
Expr_Unidade Indica as unidades para uma Expr. Todos os nomes das unidades têm de começar por um carácter de sublinhado. Pode utilizar unidades predefinidas ou criar as suas próprias unidades. Para uma lista de unidades predefinidas, abra o Catálogo e veja o separador Conversões de unidades. Pode seleccionar os nomes das unidades do Catálogo ou escrever os nomes das unidades directamente. |
Nota: Pode encontrar o símbolo de conversão, 4, no Catálogo. Clique em |
|
Variável_ Quando Variável não tiver valor, é tratada como se representasse um número complexo. Por predefinição, sem o _, a variável é tratada como real. Se Variável tiver um valor, o _ é ignorado e Variável retém o tipo de dados originais. Nota: Pode guardar um número complexo numa variável sem utilizar _. No entanto, para obter melhores resultados em cálculos como cSolve() e cZeros(), o _ é recomendado. |
Partindo do princípio que z é indefinido:
|
|
Teclas /k |
|||||||
|
Expr_Unidade1 4 _Unidade2 ÞExpr _Unidade2 Converte uma expressão de uma unidade para a outra. O carácter de sublinhado _ indica as unidades. As unidades têm de ser da mesma categoria, como, por exemplo, Comprimento ou Área. Para uma lista de unidades predefinidas, abra o Catálogo e veja o separador Conversões de unidades:
Pode também escrever os nomes das unidades manualmente. Para escrever “_” quando escrever os nomes das unidades na unidade portátil, prima /_. Nota: Para converter as unidades de temperatura, utilize tmpCnv() e @tmpCnv(). O operador de conversão 4 não processa unidades de temperatura. |
|
|
Catálogo > |
|
|
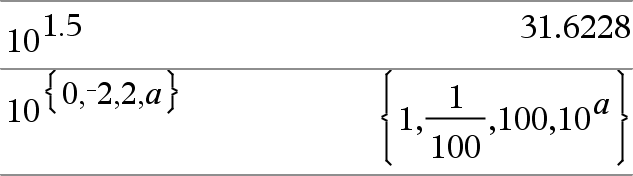
10^(Expr1) Þexpressão 10^(Lista1) Þlista Devolve 10 elevado à potência do argumento. Para uma lista, devolve 10 elevado à potência dos elementos em Lista1. |
|
|
10^(MatrizQuadrada1) ÞMatrizQuadrada Devolve 10 elevado à potência de MatrizQuadrada1. Isto não é o mesmo que calcular 10 elevado à potência de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
|
|
Catálogo > |
|
|
Lista1 ^/Þlista Devolve o recíproco do argumento. Para uma lista, devolve os recíprocos dos elementos em Lista1. |
|
|
MatrizQuadrada1 ^/ÞMatrizQuadrada Devolve o inverso de MatrizQuadrada1. MatrizQuadrada1 tem de ser uma matriz quadrada não singular. |
|
|
Teclas /k |
||||||||||
|
Expr | ExprBooleana1 [ Expr | ExprBooleana1 [ O símbolo de limite (“|”) serve como um operador binário. O operando à esquerda de | é uma expressão. O operando à direita de | especifica uma ou mais relações que servem para afetar a simplificação da expressão. Várias relações após | têm de ser reunidas por operadores “ O operador de limite fornece três tipos de funcionalidades básicas:
|
|
|||||||||
|
As substituições estão na forma de uma igualdade, como x=3 ou y=sin(x). Para ser mais eficaz, o membro esquerdo deve ser uma variável simples. Expr | Variável = valor substituem valor para todas as ocorrências de Variável em Expr. |
|
|||||||||
|
Os limites de intervalos tomam a forma de uma ou mais desigualdades reunidas pelos operadores “and” ou “or” lógicos. Os limites de intervalos também permitem a simplificação que caso contrário pode ser inválida ou não calculável. |
|
|||||||||
|
As exclusões utilizam o operador relacional “diferentes” (/= ou ƒ) para excluir um valor específico de consideração. |
|
|
Teclas /h |
|
|
Lista & Var Matriz & Var Expr & Função(Parâm1,...) Lista & Função(Parâm1,...) Matriz & Função(Parâm1,...) Se a variável Var não existir, cria-a e inicia-a para Expr, Lista ou Matriz. Se a variável Var já existir e não estiver bloqueada nem protegida, substitui o conteúdo por Expr, Lista ou Matriz. Sugestão: Se planear fazer cálculos simbólicos com variáveis indefinidas, evite guardar o quer que seja nas variáveis de uma letra mais utilizadas, como a, b, c, x, y, z, e por aí adiante. Nota: Pode introduzir este operador através da escrita de =: no teclado como um atalho. Por exemplo, escreva pi/4 =: myvar. |
|
|
Teclas /t |
|
|
Var := Lista Var := Matriz Função(Parâm1,...) := Expr Função(Parâm1,...) := Lista Função(Parâm1,...) := Matriz Se a variável Var não existir, cria Var e inicia-a para Expr, Lista ou Matriz. Se Var já existir e não estiver bloqueada nem protegida, substitui o conteúdo por Expr, Lista ou Matriz.
|
|
|
Teclas /k |
|
|
© [ texto] © processa texto como uma linha de comentário, permitindo anotar as funções e os programas criados. © pode estar no início ou em qualquer parte da linha. Tudo à direita de ©, no fim da linha, é o comentário. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
|
|
Teclas 0B, teclas 0H |
|
|
0b NúmeroBinário 0h NúmeroHexadecimal Indica um número binário ou hexadecimal, respectivamente. Para introduzir um número binário ou hexadecimal, utilize sempre o prefixo 0b ou 0h independentemente do modo Base. Sem um prefixo, um número é tratado como decimal (base 10). Os resultados aparecem de acordo com o modo base. |
No modo base Dec:
No modo base Bin:
No modo base Hex:
|








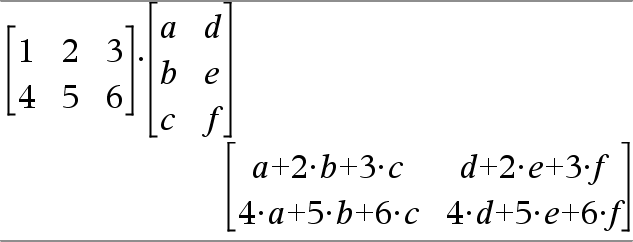












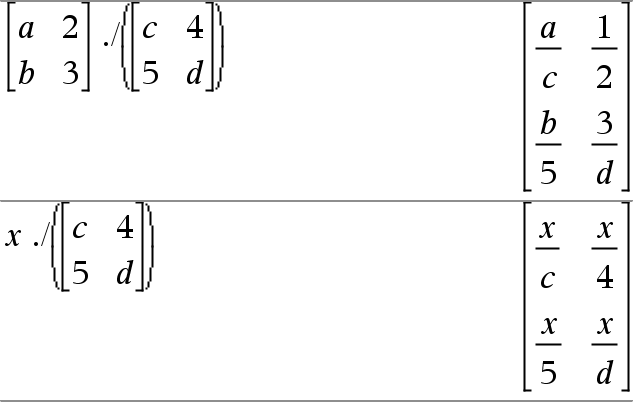

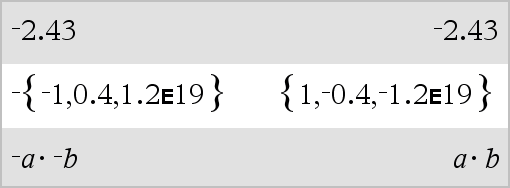
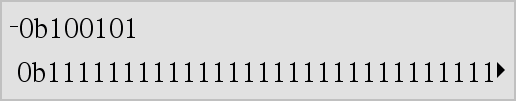
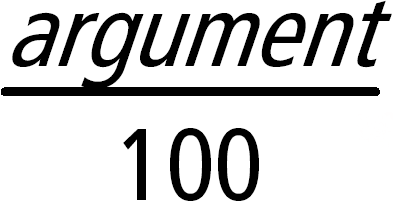
 .
.


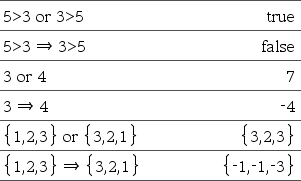
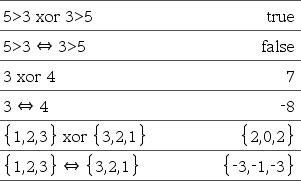



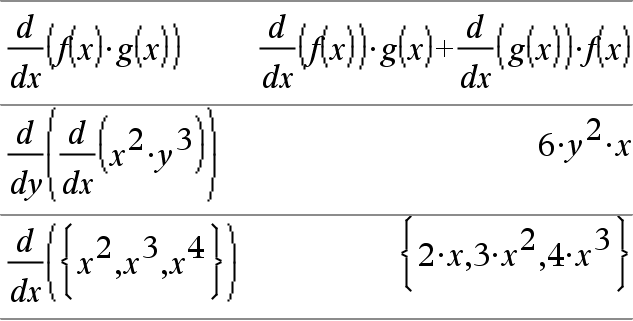


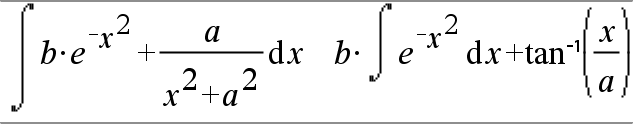

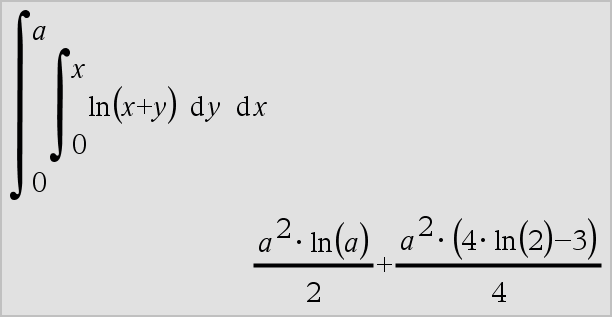

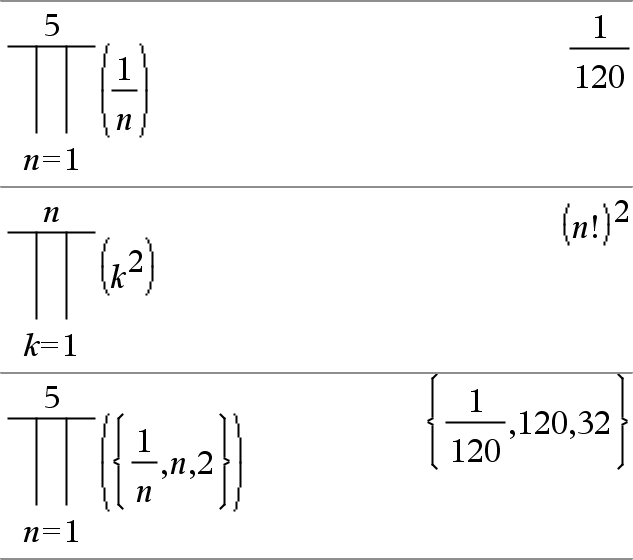

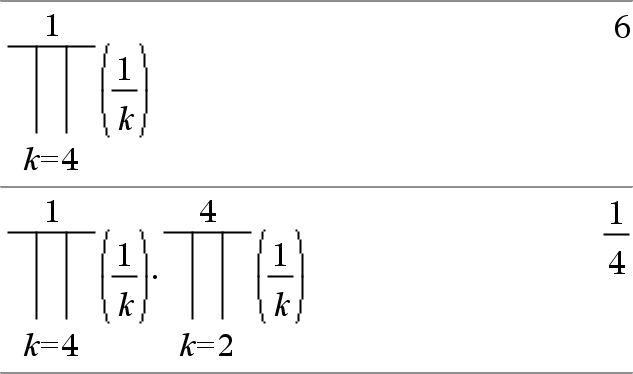
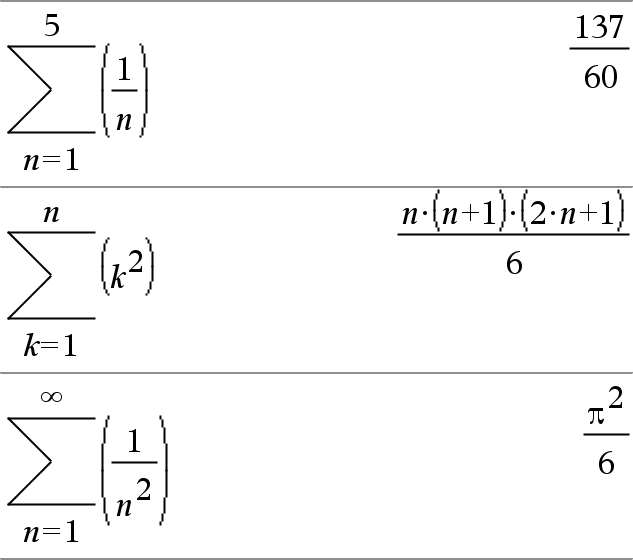

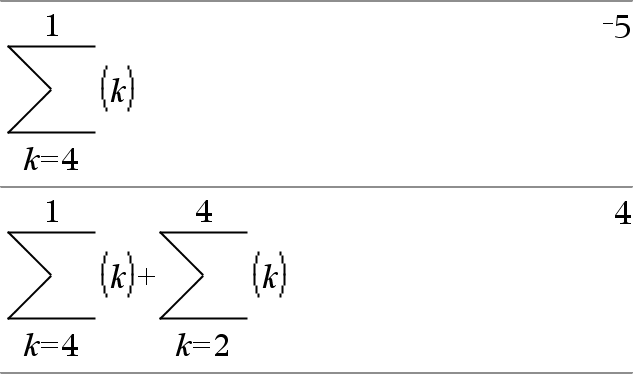
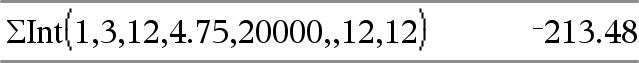
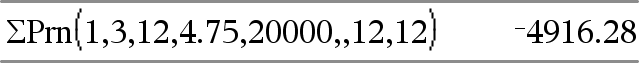







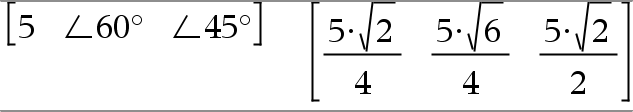
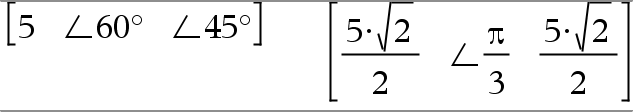

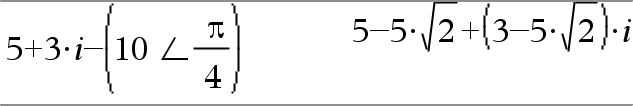
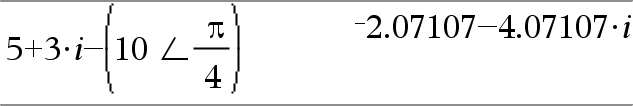
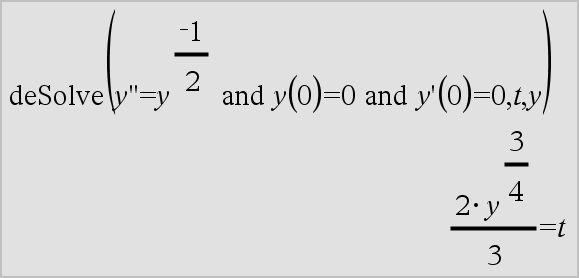

 e, em seguida, em
e, em seguida, em