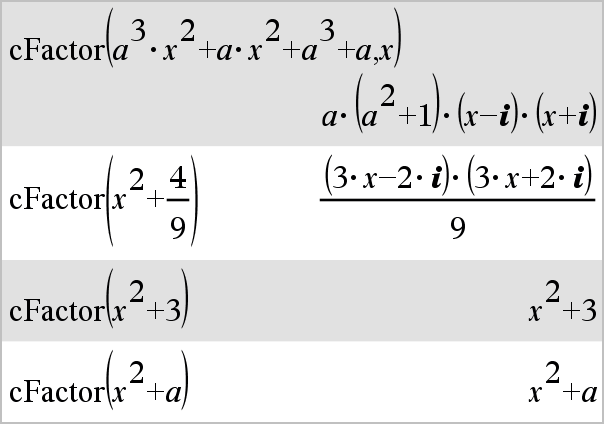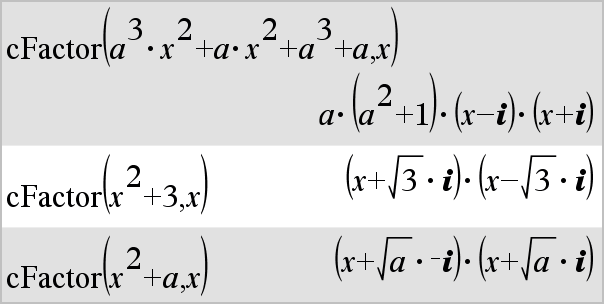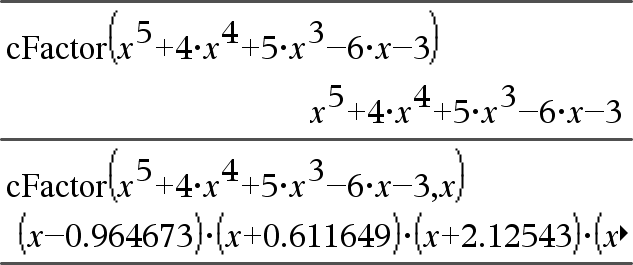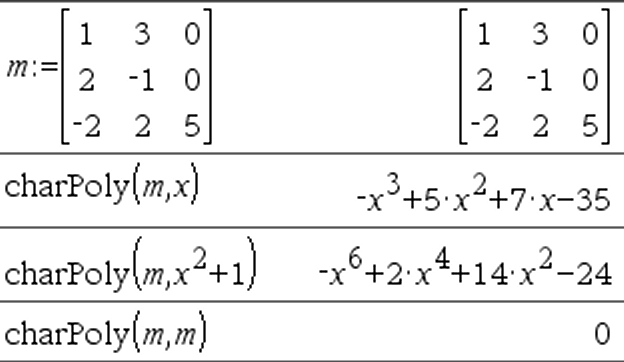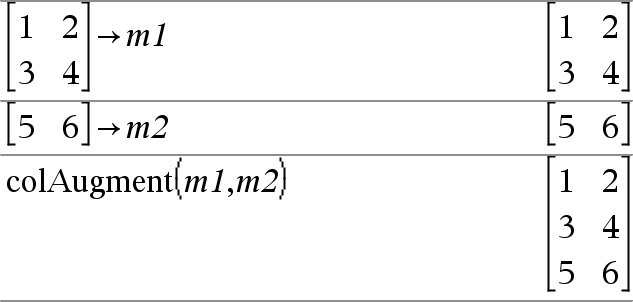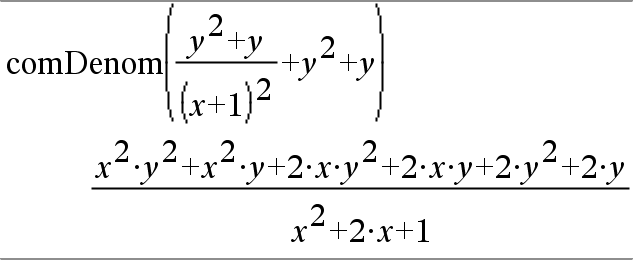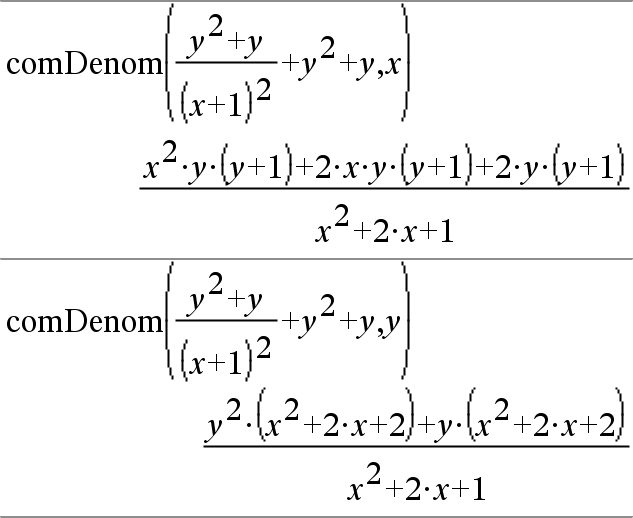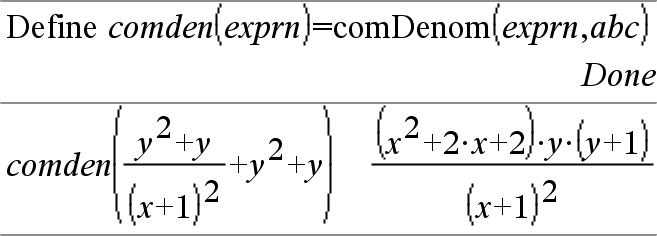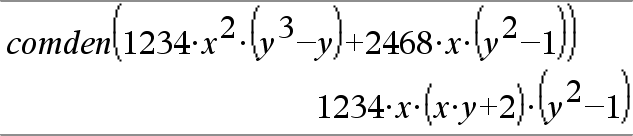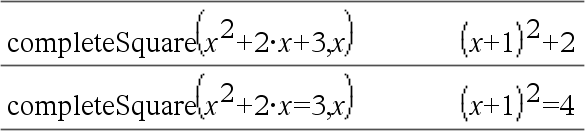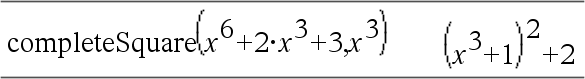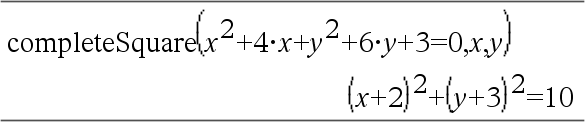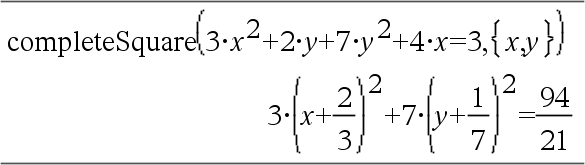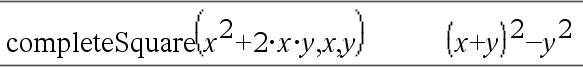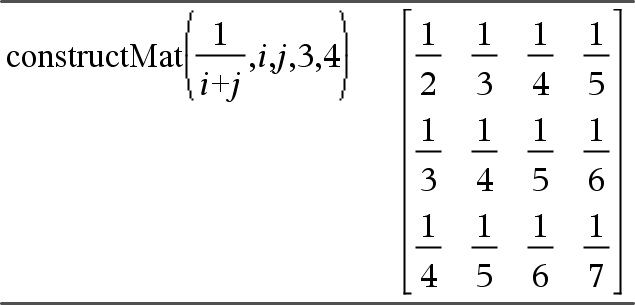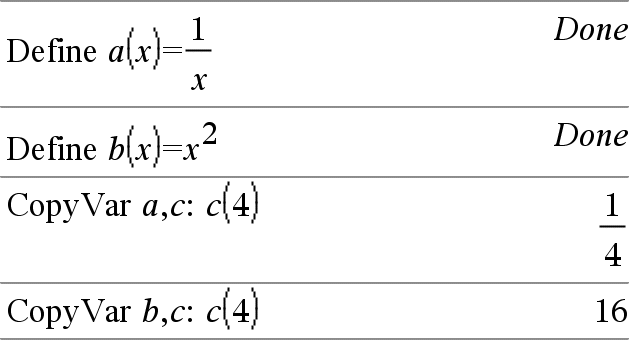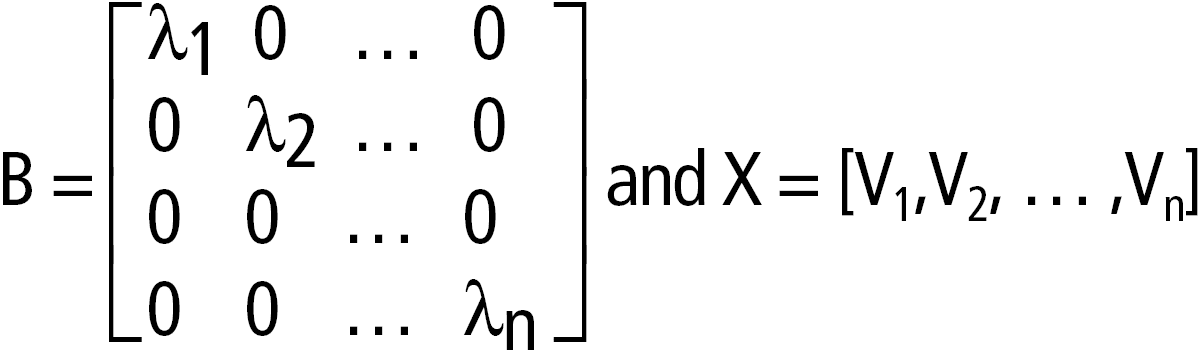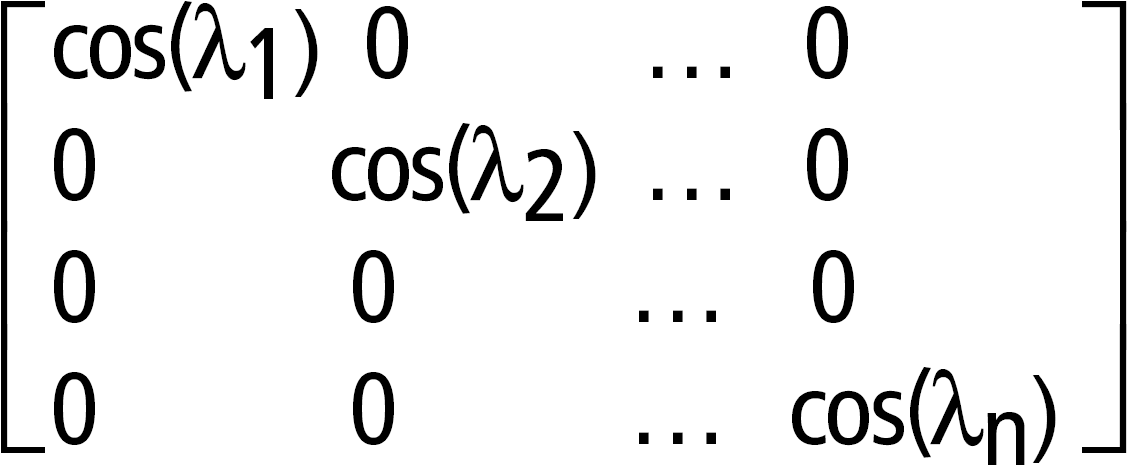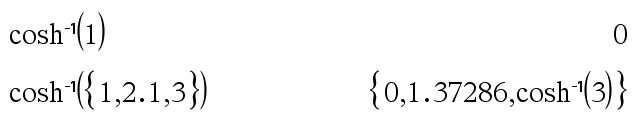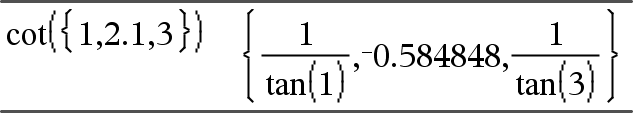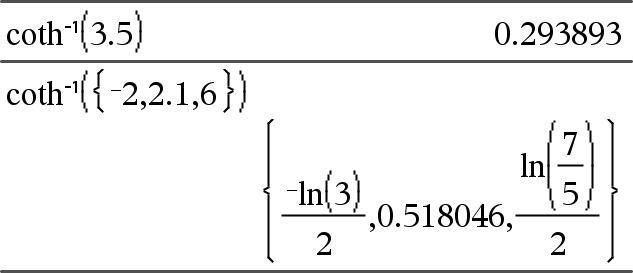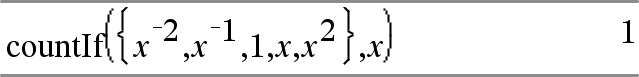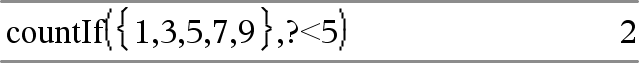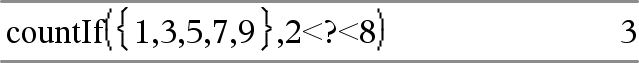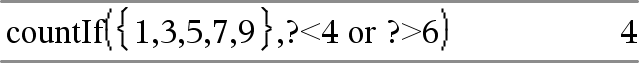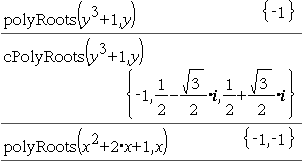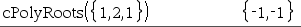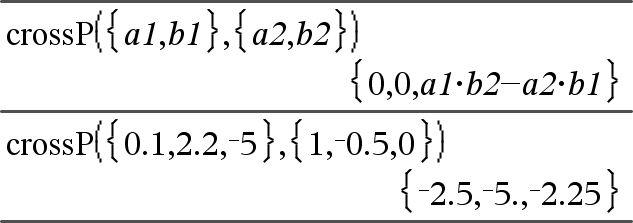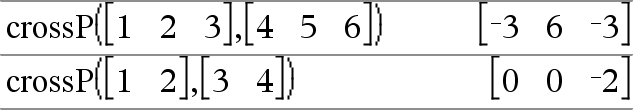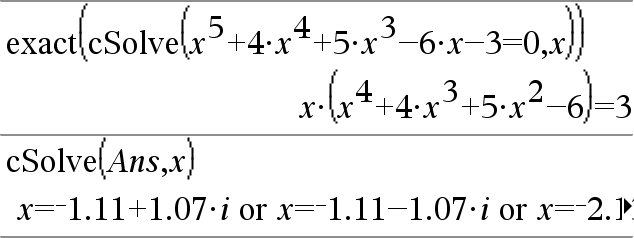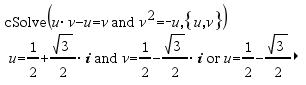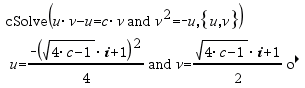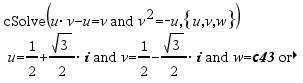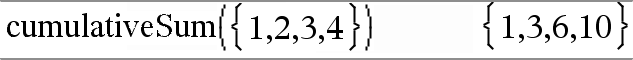|
Catálogo > |
|
|
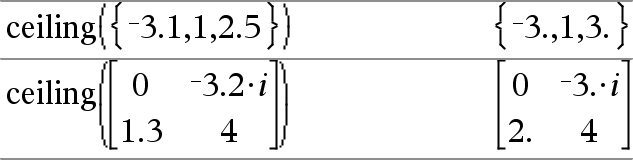
ceiling(Expr1) Þnúmero inteiro Devolve o número inteiro mais próximo que é | o argumento. O argumento pode ser um número complexo ou real. Nota: Consulte também floor(). |
|
|
ceiling(Lista1) Þlista ceiling(Matriz1) Þmatriz Devolve uma lista ou matriz do ceiling de cada elemento. |
|
|
Catálogo > |
|
|
Devolve a derivada numérica com a fórmula do quociente da diferença central. Ao especificar o Valor, substitui qualquer atribuição de variável anterior ou qualquer substituição atual “|” para a variável. Passo é o valor do passo. Se omitir Passo, predefine-se para 0,001. Quando utilizar Lista1 ou Matriz1 , a operação é mapeada através dos valores da lista ou dos elementos da matriz. Nota: Consulte também avgRC() |
|
|
Catálogo > |
|
|
cFactor(Expr1 [, Var ]) Þexpressão cFactor(Lista1 [, Var ]) Þlista cFactor(Matriz1 [, Var ]) Þmatriz
cFactor(Expr1) devolve Expr1 decomposta em factores em relação a todas as variáveis sobre um denominador comum. Expr1 é decomposta o mais possível em factores racionais lineares mesmo que isto introduza novos números não reais. Esta alternativa é adequada se quiser a factorização em relação a mais do que uma variável. |
|
|
cFactor(Expr1, Var) devolve Expr1 decomposta em factores em relação à variável Var. Expr1 é decomposta o mais possível em factores que são lineares em Var, com talvez constantes não reais, mesmo que introduza subexpressões ou constantes irracionais que são irracionais noutras variáveis. Os factores e os termos são ordenados com Var como variável principal. As potências similares de Var são recolhidas em cada factor. Inclua Var se a factorização for necessária em relação apenas a essa variável e estiver disposto a aceitar expressões irracionais em qualquer outra variável para aumentar a factorização em relação a Var. Pode existir alguma decomposição em factores incidental em relação a outras variáveis. |
|
|
Para a definição Auto do modo Auto ou Aproximado, incluindo Var, permite também a aproximação a coeficientes de pontos flutuantes em que os coeficientes irracionais não podem ser expressos explicitamente em termos das funções integradas. Mesmo quando exista apenas uma variável, incluindo Var, pode produzir a factorização mais completa. Nota: Consulte também factor(). |
Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. |
|
Catálogo > |
|
|
char(Número inteiro) Þcarácter Devolve uma cadeia de caracteres com o carácter numerado Número inteiro a partir do conjunto de caracteres da unidade portátil. O intervalo válido para o Número inteiro é 0–65535. |
|
|
Catálogo > |
|
|
charPoly(MatrizQuadrada,Var)Þexpressão polinomial charPoly(MatrizQuadrada,Expr)Þexpressão polinomial charPoly(MatrizQuadrada1,Matriz2)Þexpressão polinomial Devolve o polinómio característico de MatrizQuadrada. O polinómio característico de n×n matriz A, indicado por pA(l), é o polinómio definido por pA(l) = det(l• I NA) em que I indica a matriz identidade n×n. MatrizQuadrada1 e MatrizQuadrada2 têm de ter as dimensões iguais. |
|
|
Catálogo > |
|
|
c22way MatrizObs chi22way MatrizObs Calcula um teste c 2para associação à tabela de contagens bidireccional na matriz observada MatrizObs. Um resumo dos resultados é guardado na variável stat.results (aqui). Para mais informações sobre o efeito dos elementos vazios numa matriz, consulte “Elementos (nulos) vazios” (aqui). |
|
|
Variável de saída |
Descrição |
|
stat.c2 |
Estatística do Qui quadrado: soma (observada - prevista) 2 /prevista |
|
stat.PVal |
Menor nível de significância para o qual a hipótese nula pode ser rejeitada |
|
stat.df |
Graus de liberdade para a estatística do Qui quadrado |
|
stat.ExpMat |
Matriz da tabela de contagem de elementos previsto, assumindo a hipótese nula |
|
stat.CompMat |
Matriz de contribuições da estatística do Qui quadrado dos elementos |
|
Catálogo > |
|
|
c2Cdf(LimiteInferior,LimiteSuperior,df)Þnúmero se LimiteInferior e LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem listas chi2Cdf(LimiteInferior,LimiteSuperior,df)Þnúmero se LimiteInferior e LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem listas Calcula a probabilidade de distribuição c2 entre LimiteInferior e LimiteSuperior para os graus de liberdade especificados df. Para P(X { LimiteSuperior), defina LimiteInferior = 0. Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (aqui). |
|
|
Catálogo > |
|
|
c2GOF Lista obs, Lista exp, df chi2GOF Lista obs, Lista exp, df Efectua um teste para confirmar que os dados da amostra são de uma população que está em conformidade com uma distribuição especificada. Um resumo dos resultados é guardado na variável stat.results (aqui). Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (aqui). |
|
|
Variável de saída |
Descrição |
|
stat.c2 |
Estatística do Qui quadrado: soma((observada - prevista) 2 /prevista |
|
stat.PVal |
Menor nível de significância para o qual a hipótese nula pode ser rejeitada |
|
stat.df |
Graus de liberdade para a estatística do Qui quadrado |
|
stat.CompList |
Matriz de contribuições da estatística do Qui quadrado dos elementos |
|
Catálogo > |
|
|
c2Pdf(ValX,df)Þnúmero se ValX for um número, lista se ValX for uma lista chi2Pdf(ValX,df)Þnúmero se ValX for um número, lista se ValX for uma lista Calcula a função de densidade de probabilidade (pdf) para a distribuição c2 num valor ValX especificado para os graus de liberdade especificados df. Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (aqui). |
|
|
Catálogo > |
|
|
ClearAZ Apaga todas as variáveis de um carácter no espaço do problema actual. Se uma ou mais variáveis estiverem bloqueadas, este comando mostra uma mensagem de erro e só elimina as variáveis desbloqueadas. Consulte |
|
|
Catálogo > |
|
|
Apaga o estado de erro e define a variável do sistema errCode para zero. A proposição Else do bloco Try...Else...EndTry deve utilizar ClrErr ou PassErr. Se tiver de processar ou ignorar o erro, utilize ClrErr. Se não souber o que fazer com o erro, utilize PassErr para o enviar para a rotina de tratamento de erros seguinte. Se não existirem mais rotinas de tratamento de erros Try...Else...EndTry pendente, a caixa de diálogo de erros aparecerá como normal. Nota: Consulte também PassErr, aqui, e Try, aqui. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
Para ver um exemplo de ClrErr, consulte o exemplo 2 no comando Try, aqui.
|
|
Catálogo > |
|
|
colAugment(Matriz1, Matriz2) Þmatriz Devolve uma nova lista que é a Matriz2 acrescentada ao fim da Matriz1. As matrizes têm de ter dimensões de colunas iguais, e a Matriz2 é acrescentada à Matriz1 como novas colunas. Não altere Matriz1 ou Matriz2. |
|
|
Catálogo > |
|
|
colDim(Matriz) Þexpressão Devolve o número de colunas contidas em Matriz. Nota: Consulte também rowDim(). |
|
|
Catálogo > |
|
|
colNorm(Matriz) Þexpressão Devolve o máximo das somas dos valores absolutos dos elementos nas colunas em Matriz. Nota: Os elementos da matriz indefinidos não são permitidos. Consulte também rowNorm(). |
|
|
Catálogo > |
|
|
comDenom(Expr1 [, Var ]) Þexpressão comDenom(Lista1 [, Var ]) Þlista comDenom(Matriz1 [, Var ]) Þmatriz
comDenom(Expr1) devolve uma fracção simplificada com um numerador completamente expandido sobre um denominador completamente expandido. |
|
|
comDenom(Expr1, Var) devolve um rácio reduzido do numerador e do denominador expandidos em relação a Var. Os termos e os factores são ordenados com Var como variável principal. As potências similares de Var são recolhidas. Pode existir alguma decomposição em factores incidental dos coeficientes recolhidos. Comparada para omitir Var, esta poupa tempo frequentemente, memória e espaço no ecrã, enquanto torna a expressão mais compreensível. Torna também as operações subsequentes no resultado mais rápidas e poupa a memória. |
|
|
Se Var não ocorrer em Expr1, comDenom(Expr1, Var) devolve uma fracção simplificada com um numerador não expandido sobre um denominador não expandido. Estes resultados poupam geralmente mais tempo, memória e espaço no ecrã. Estes resultados decompostos parcialmente tornam também as operações subsequentes no resultado mais rápidas e poupam a memória. |
|
|
Mesmo quando não exista um denominador, a função comden é frequentemente uma forma rápida para alcançar a factorização parcial se factor() for muito lento ou se esgotar a memória. Sugestão: Introduza esta definição da função comden() e experimente-a rotinamente como uma alternativamente para comDenom() e factor(). |
|
|
Catálogo > |
|
|
Converte uma expressão polinomial quadrática da forma a·x2+b·x+c para a forma a·(x-h)2+k ou Converte uma equação do 2º grau da forma a·x2+b·x+c=d para a forma a·(x-h)2=k O primeiro argumento tem de ser uma expressão quadrática ou equação na forma padrão, em relação ao segundo argumento. O segundo argumento tem de ser um único termo de uma só variável ou um único termo de uma só variável elevado a uma potência racional, por exemplo x, y2 ou z(1/3). A terceira e quarta expressões de sintaxe para concluir o quadrado nas variáveis Var1, Var2 [,… ]). |
|
|
Catálogo > |
|
|
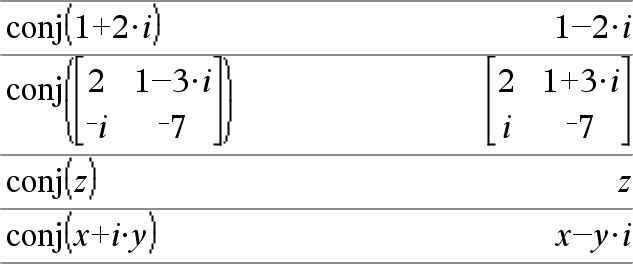
conj(Expr1) Þexpressão conj(Lista1) Þlista conj(Matriz1) Þmatriz Devolve o conjugado complexo do argumento. Nota: Todas as variáveis indefinidas são tratadas como variáveis reais. |
|
|
Catálogo > |
|
|
constructMat(Expr,Var1,Var2,NúmLinhas,NúmColunas) Þmatriz Devolve uma matriz de acordo com os argumentos. Expr é uma expressão nas variáveis Var1 e Var2. Os elementos da matriz resultante são formados através da avaliação de Expr para cada valor incrementado de Var1 e Var2. Var1 é incrementada automaticamente de 1 a NúmLinhas. Em cada linha, Var2 é incrementada de 1 a NúmColunas. |
|
|
Catálogo > |
|
|
CopyVar Var1, Var2 CopyVar Var1., Var2. CopyVar Var1, Var2 copia o valor da variável Var1 à variável Var2, criando Var2, se for necessário. A variável Var1 tem de ter um valor. Se Var1 for o nome de uma função definida pelo utilizador existente, copia a definição dessa função para a função Var2. A função Var1 tem de ser definida. Var1 tem de cumprir os requisitos de nomeação de variáveis ou tem de ser uma expressão indirecta que se simplifica para um nome de variável que cumpra os requisitos. |
|
|
CopyVar Var1., Var2. copia todos os membros da Var1. grupo de variáveis para a Var2. grupo, criando Var2. se for necessário. Var1. tem de ser o nome de um grupo de variáveis existentes, como, por exemplo, o da estatística stat.nn resultados ou variáveis criados com a função |
|
|
Catálogo > |
|
|
corrMat(Lista1, Lista2 [, …[, Lista20 ]]) Calcula a matriz de correlação para a matriz aumentada [ Lista1, Lista2, ..., Lista20 ]. |
|
|
Catálogo > |
|
|
Expr 4cos Nota: Pode introduzir este operador através da escrita de @>cos no teclado do computador. Representa Expr em função do co-seno. Este é um operador de conversão. Apenas pode ser utilizado no fim da linha de entrada. 4cos reduz todas as potências de sin(...) módulo 1Ncos(...)^2 para quaisquer polinómios residuais de potências de cos(...) tenham expoentes no intervalo [0, 2]. Por conseguinte, o resultado ficará livre de sin(...) se e só se sin(...) ocorrer na expressão fornecida apenas em potências pares. Nota: Este operador de conversão não é suportado nos modos de ângulos Graus ou Grados. Antes de o utilizar, certifique-se de que o modo Ângulo está definido para Radianos e que Expr não contém referências explícitas a ângulos em graus ou grados. |
|
|
Tecla µ |
|
|
cos(Expr1) Þexpressão cos(Lista1) Þlista
cos(Lista1) devolve uma lista de co-senos de todos os elementos na Lista1. Nota: O argumento é interpretado como um ângulo express em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Pode utilizar ¡, G ou R para substituir o modo de ângulo temporariamente. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
cos(MatrizQuadrada1) ÞMatriz quadrada Devolve o co-seno da matriz da MatrizQuadrada1. Isto não é o mesmo que calcular o co-seno de cada elemento. Quando uma função escalar f(A) operar na MatrizQuadrada1 (A), o resultado é calculado pelo algoritmo: Calcule os valores próprios (li) e os vectores próprios (Vi) de A. MatrizQuadrada1 tem de ser diagnolizável. Também não pode ter variáveis simbólicas sem um valor. Forme as matrizes:
A = X B X /e f(A) = X f(B) X /. Por exemplo, cos(A) = X cos(B) X / em que: cos(B) =
Todos os cálculos são efectuados com a aritmética de ponto flutuante. |
No modo de ângulo Radianos:
|
|
Tecla µ |
|
|
cos/(Expr1) Þexpressão cos/(Lista1) Þlista
cos/(Lista1) devolve uma lista de co-senos inversos de cada elemento de Lista1. Nota: O resultado é devolvido como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Nota: Pode introduzir esta função através da escrita de arccos(...) no teclado. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
cos/(MatrizQuadrada1) ÞMatriz quadrada Devolve o co-seno inverso da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o co-seno inverso de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
No modo de ângulo Radianos e Formato complexo rectangular:
Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. |
|
Catálogo > |
|
|
cosh(Expr1) Þexpressão cosh(Lista1) Þlista
cosh (Lista1) devolve uma lista dos co-senos hiperbólicos de cada elemento de Lista1. |
No modo de ângulo Graus:
|
|
cosh (MatrizQuadrada1) ÞMatriz quadrada Devolve o co-seno hiperbólico da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o co-seno hiperbólico de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
cosh/(Expr1) Þexpressão cosh/(Lista1) Þlista
cosh/(Lista1) devolve uma lista dos co-senos hiperbólicos inversos de cada elemento de Lista1. Nota: Pode introduzir esta função através da escrita de arccosh(...) no teclado. |
|
|
cosh/(MatrizQuadrada1) ÞMatriz quadrada Devolve o co-seno hiperbólico inverso da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o co-seno hiperbólico inverso de cada elemento. Para mais informações sobre o método de cálculo, consulte cos(). MatrizQuadrada1 tem de ser diagnolizável. O resultado contém sempre os números de ponto flutuante. |
No modo de ângulo Radianos e Formato complexo rectangular:
Para ver o resultado completo, prima 5 e, de seguida, utilize 7 e 8 para mover o cursor. |
|
Tecla µ |
|
|
cot(Expr1) Þ expressão cot(Lista1) Þ lista Devolve a co-tangente de Expr1 ou devolve uma lista das co-tangentes de todos os elementos em Lista1. Nota: O argumento é interpretado como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Pode utilizar ¡, G ou R para substituir o modo de ângulo temporariamente. Nota: Pode introduzir esta função através da escrita de arccot(...) no teclado. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
Tecla µ |
|
|
cot/(Expr1) Þexpressão cot/(Lista1) Þlista Devolve o ângulo cuja co-tangente é Expr1 ou devolve uma lista com as co-tangentes inversas de cada elemento de Lista1. Nota: O resultado é devolvido como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
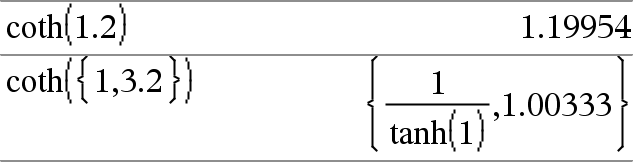
coth(Expr1) Þexpressão coth(Lista1) Þlista Devolve a co-tangente hiperbólica de Expr1 ou devolve uma lista das co-tangentes hiperbólicas de todos os elementos de List1. |
|
|
Catálogo > |
|
|
coth/(Expr1) Þexpressão coth/(Lista1) Þlista Devolve a co-tangente hiperbólica inversa de Expr1 ou devolve uma lista com as co-tangentes hiperbólicas inversas de cada elemento de Lista1. Nota: Pode introduzir esta função através da escrita de arccoth(...) no teclado. |
|
|
Catálogo > |
|
|
count(Valor1ouLista1 [, Valor2ouLista2 [,...]]) Þvalor Devolve a contagem acumulada de todos os elementos nos argumentos que se avaliam para valores numéricos. Cada argumento pode ser uma expressão, valor, lista ou matriz. Pode misturar tipos de dados e utilizar argumentos de várias dimensões. Para uma lista, matriz ou intervalo de dados, cada elemento é avaliado para determinar se deve ser incluído na contagem. Na aplicação Listas e Folha de cálculo, pode utilizar um intervalo de células no lugar de qualquer argumento. Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
No último exemplo, apenas 1/2 e 3+4* i são contados. Os restantes argumentos, partindo do princípio que x é indefinido, não se avaliam para valores numéricos. |
|
Catálogo > |
|||||||
|
countif(Lista, Critérios) Þvalor Devolve a contagem acumulada de todos os elementos em Lista que cumpram os critérios especificados. Critérios podem ser:
Na aplicação Listas e Folha de cálculo, pode utilizar um intervalo de células no lugar de Lista. Os elementos (nulos) vazios da lista são ignorados. Para mais informações sobre os elementos vazios, consulte aqui. |
Conta o número de elementos igual a 3.
Conta o número de elementos igual a “def.”
Conta o número de elementos igual a x; este exemplo assume que a variável x é indefinida.
Conta 1 e 3.
Conta 3, 5, e 7.
Conta 1, 3, 7 e 9. |
|
Catálogo > |
|
|
A primeira sintaxe,
A segunda sintaxe, Nota: Consulte também |
|
|
Catálogo > |
|
|
crossP(Lista1, Lista2) Þlista Devolve o produto cruzado de Lista1 e Lista2 como uma lista. Lista1 e Lista2 têm de ter dimensões iguais e a dimensão tem de ser 2 ou 3. |
|
|
crossP(Vector1, Vector2) Þvector Devolve um vector da linha ou coluna (dependendo dos argumentos) que é o produto cruzado de Vector1 e Vector2. Vector1 e Vector2 têm de ser vectores de linhas ou ambos têm de ser vectores de colunas. Ambos os vectores têm de ter dimensões iguais e a dimensão tem de ser 2 ou 3. |
|
|
Tecla µ |
|
|
csc(Expr1) Þexpressão csc(Lista1) Þlista Devolve a co-secante de Expr1 ou devolve uma lista com as co-secantes de todos os elementos em Lista1. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
Tecla µ |
|
|
csc/(Expr1) Þ expressão csc/(Lista1) Þ lista Devolve o ângulo cuja co-secante é Expr1 ou devolve uma lista com as co-secantes inversas de cada elemento de Lista1. Nota: O resultado é devolvido como um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Nota: Pode introduzir esta função através da escrita de arccsc(...) no teclado. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
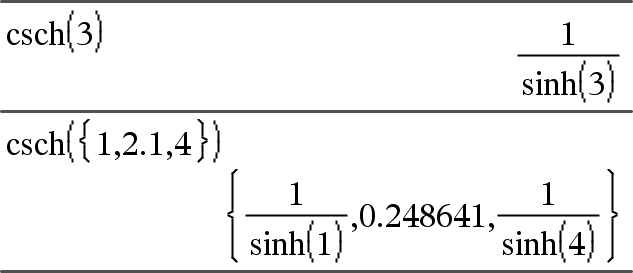
csch(Expr1) Þ expressão csch(Lista1) Þ lista Devolve a co-secante hiperbólica de Expr1 ou devolve uma lista das co-secantes hiperbólicas de todos os elementos de List1. |
|
|
Catálogo > |
|
|
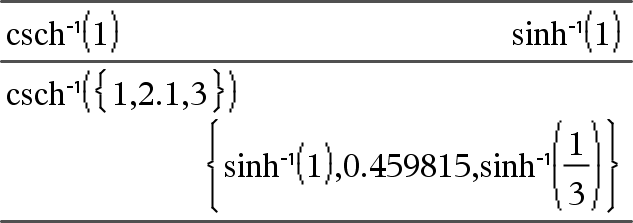
csch/(Expr1) Þ expressão csch/(Lista1) Þ lista Devolve a co-secante hiperbólica inversa de Expr1 ou devolve uma lista com as co-secantes hiperbólicas inversas de cada elemento de Lista1. Nota: Pode introduzir esta função através da escrita de arccsch(...) no teclado. |
|
|
Catálogo > |
|
|
CubicReg X, Y[, [Freq] [, Categoria, Incluir]] Calcula a regressão polinomial cúbicay = a·x3+b· x2+c·x+da partir das listas X e Y com a frequência Freq. Um resumo dos resultados é guardado na variável stat.results (aqui). Todas as listas têm de ter a mesma dimensão, excepto para Incluir. X e Y são listas de variáveis independentes e dependentes. Freq é uma lista opcional de valores de frequência. Cada elemento em Freq especifica a frequência de ocorrência para cada ponto de dados X e Y correspondente. O valor predefinido é 1. Todos os elementos têm de ser números inteiros | 0. Categoria é uma lista de códigos de categorias para os dados X e Y correspondentes. Incluir é uma lista de um ou mais códigos de categorias. Apenas os itens de dados cujo código de categoria está incluído nesta lista são considerados no cálculo. Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (aqui). |
|
|
Variável de saída |
Descrição |
|
stat.RegEqn |
Equação de regressão: a · x 3 +b · x 2 +c · x+d |
|
stat.a, stat.b, stat.c, stat.d |
Coeficientes de regressão |
|
stat.R2 |
Coeficiente de determinação |
|
stat.Resid |
Resíduos da regressão |
|
stat.XReg |
Lista de pontos de dados na Lista X modificada utilizada na regressão com base em restrições de Freq, Lista de categorias e Incluir categorias |
|
stat.YReg |
Lista de pontos de dados na Lista Y modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias |
|
stat.FreqReg |
Lista de frequências correspondentes a stat.XReg e stat.YReg |
|
Catálogo > |
|
|
cumulativeSum(Lista1)Þlista Devolve uma lista das somas acumuladas dos elementos em Lista1, começando no elemento 1. |
|
|
cumulativeSum(Matriz1)Þmatriz Devolve uma matriz das somas cumulativas dos elementos em Matriz1. Cada elemento é a soma cumulativa da coluna de cima a baixo. Um elemento (nulo) vazio em Lista1 ou em Matriz1 produz um elemento nulo na matriz ou lista resultante. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Catálogo > |
|
|
Cycle Transfere o controlo imediatamente para a iteração seguinte do ciclo actual (For, While ou Loop). Cycle não é permitido fora das três estruturas em espiral (For, While ou Loop). Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
Lista de funções que soma os números inteiros de 1 a 100 ignorando 50.
|
|
Catálogo > |
|
|
Vector 4Cylind Nota: Pode introduzir este operador através da escrita de @>Cylind no teclado do computador. Apresenta o vector da linha ou coluna em forma cilíndrica [r, ±q, z]. Vector tem de ter exactamente três elementos. Pode ser uma linha ou coluna. |
|