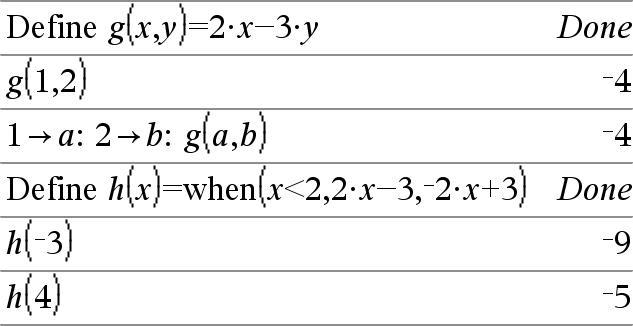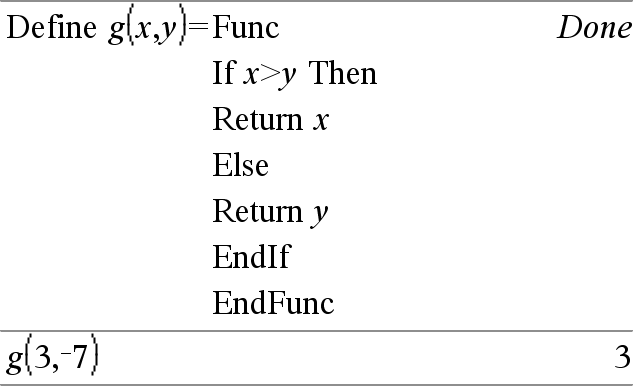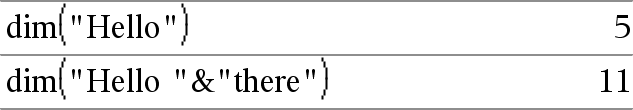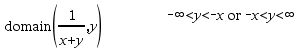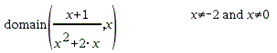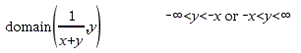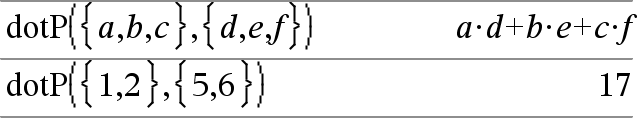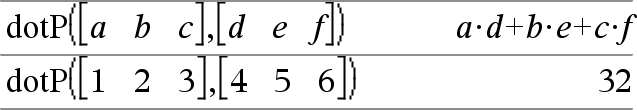|
Catálogo > |
|
|
dbd(data1,data2) Þvalor Devolve o número de dias entre data1 e data2 com o método de contagem de dias actual. data1 e data2 podem ser números ou listas de números no intervalo das datas no calendário padrão. Se data1 e data2 forem listas, têm de ter o mesmo comprimento. data1 e data2 têm de estar entre os anos 1950 e 2049. Pode introduzir as datas num de dois formatos. A colocação decimal diferencia-se entre os formatos de data. MM.AAAA (formato utilizado nos Estados Unidos) DDMM.AA (formato utilizado na Europa) |
|
|
Catálogo > |
|
|
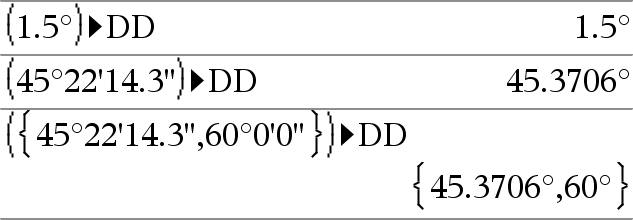
Expr1 4DD Þvalor Lista1 4DD Þlista Matriz1 4DD Þmatriz Nota: Pode introduzir este operador através da escrita de @>DD no teclado do computador. Devolve o decimal equivalente do argumento expresso em graus. O argumento é um número, uma lista ou uma matriz que é interpretada pela definição do modo ângulo em gradianos, radianos ou graus. |
No modo de ângulo Graus:
No modo de ângulo Gradianos:
No modo de ângulo Radianos:
|
|
Catálogo > |
|
|
Lista1 4Decimal Þexpressão Matriz1 4Decimal Þexpressão Nota: Pode introduzir este operador através da escrita de @>Decimal no teclado do computador. Mostra o argumento em forma decimal. Este operador só pode ser utilizado no fim da linha de entrada. |
|
|
Catálogo > |
|
|
Define Var = Expressão Define Função(Parâm1, Parâm2, ...) = Expressão Define a variável Var ou a função Função definida pelo utilizador. Os parâmetros como, por exemplo, Parâm1, fornecem marcadores para argumentos de passagem para a função. Quando chamar uma função definida pelo utilizador, tem de fornecer os argumentos (por exemplo, valores ou variáveis) correspondentes aos parâmetros. Quando chamada, a função avalia a Expressão com os argumentos fornecidos. Var e Função não podem ter o nome de uma variável do sistema, um comando ou uma função integrada. Nota: Esta forma de Define é equivalente à execução da expressão: expressão & Função(Parâm1,Parâm2). |
|
|
Define Função(Parâm1, Parâm2, ...) = Func Bloco EndFunc
Define Programa(Parâm1, Parâm2, ...) = Prgm Bloco EndPrgm Desta forma, o programa ou a função definida pelo utilizador pode executar um bloco de várias afirmações. Bloco pode ser uma afirmação ou uma série de afirmações em linhas separadas. O bloco pode também incluir expressões e instruções (como, por exemplo, If, Then, Else e For). Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. Nota: Consulte também Define LibPriv, aqui, e Define LibPub, aqui. |
|
|
Catálogo > |
|
|
Define LibPriv Var = Expressão Define LibPriv Função(Parâm1, Parâm2, ...) = Expressão Define LibPriv Função(Parâm1, Parâm2, ...) = Func Bloco EndFunc Define LibPriv Programa(Parâm1, Parâm2, ...) = Prgm Bloco EndPrgm Funciona da mesma forma que Define, excepto com um programa, uma função ou uma variável da biblioteca privada. As funções e os programas privados não aparecem no Catálogo. |
|
|
Catálogo > |
|
|
Define LibPub Var = Expressão Define LibPub Função(Parâm1, Parâm2, ...) = Expressão Define LibPub Função(Parâm1, Parâm2, ...) = Func Bloco EndFunc Define LibPub Programa(Parâm1, Parâm2, ...) = Prgm Bloco EndPrgm Funciona da mesma forma que Define, excepto com um programa, uma função ou uma variável da biblioteca pública. As funções e os programas públicos aparecem no Catálogo depois de guardar e actualizar a biblioteca. |
|
|
Consulte @List(), aqui. |
|
|
|
|
|
Consulte @tmpCnv(), aqui. |
|
|
|
|
|
Catálogo > |
|
|
DelVar Var1[, Var2] [, Var3] ... DelVar Var. Elimina a variável ou o grupo de variáveis especificado da memória. Se uma ou mais variáveis estiverem bloqueadas, este comando mostra uma mensagem de erro e só elimina as variáveis desbloqueadas. Consulte |
|
|
DelVar Var. elimina todos os membros da Var. grupo de variáveis (como, por exemplo, as estatísticas stat.nn resultados ou variáveis criados com a função LibShortcut()). O ponto (.) nesta forma do comando DelVar limita-o à eliminação do grupo de variáveis; a variável simples Var não é afectada. |
|
|
Catálogo > |
|
|
Devolve uma lista com o conteúdo de Lista1 com todos os elementos (nulos) vazios removidos. Para mais informações sobre os elementos vazios, consulte aqui. |
|
|
Consulte d(), aqui. |
|
|
|
|
|
Catálogo > |
|||||||
|
det(MatrizQuadrada[, Tolerância])Þexpressão Apresenta o determinante de MatrizQuadrada. Opcionalmente, qualquer elemento da matriz é tratado como zero se o valor absoluto for inferior à Tolerância. Esta tolerância é utilizada apenas se a matriz tiver entradas de ponto flutuante e não contiver nenhuma variável simbólica sem nenhum valor atribuído. Caso contrário, Tolerância é ignorada.
|
|
|
Catálogo > |
|
|
diag(Lista) Þmatriz diag(MatrizLinha) Þmatriz diag(MatrizColuna) Þmatriz Devolve uma matriz com os valores da matriz ou da lista de argumentos na diagonal principal. |
|
|
diag(MatrizQuadrada) ÞMatrizLinha Devolve uma matriz da linha com elementos da diagonal principal de MatrizQuadrada. MatrizQuadrada tem de ser quadrada. |
|
|
Catálogo > |
|
|
dim(Lista) Þnúmero inteiro Devolve a dimensão de Lista. |
|
|
dim(Matriz) Þlista Devolve as dimensões da matriz como uma lista de dois elementos {linhas, colunas}. |
|
|
dim(Cadeia) Þnúmero inteiro Devolve o número de caracteres contidos na cadeia de caracteres Cadeia. |
|
|
Catálogo > |
|
|
Disp exprOuCadeia1 [, exprOuCadeia2 ] ... Mostra os argumentos no histórico da Calculadora. Os argumentos são apresentados em sucessão com espaços pequenos como separadores. Útil principalmente em programas e funções para garantir a visualização de cálculos intermédios. Obs para introdução do exemplo: Para obter instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto. |
|
|
Catálogo > |
|||||
|
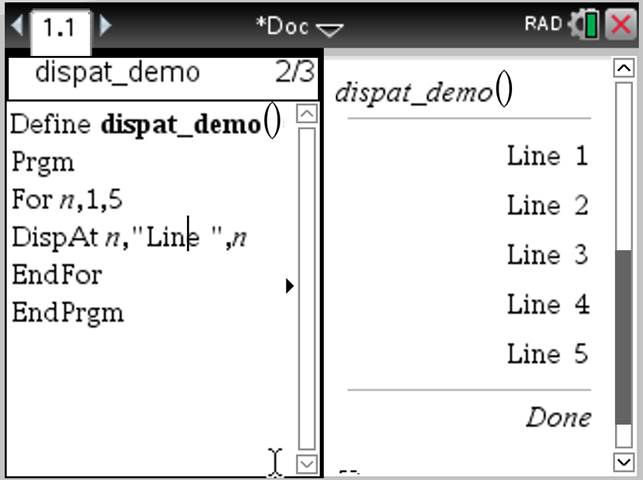
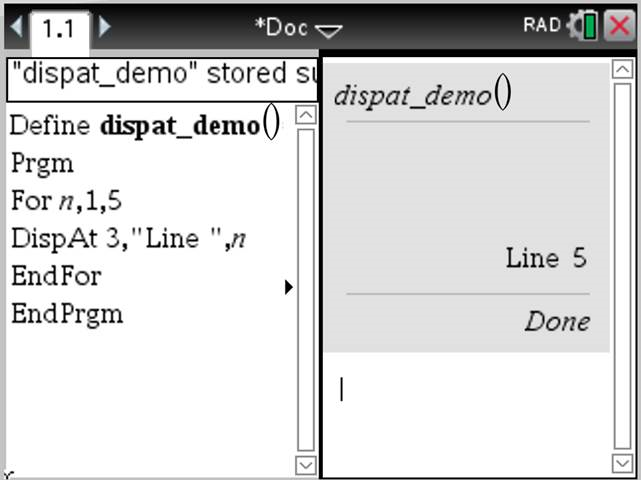
DispAt int,expr1 [,expr2 ...] ... DispAt permite-lhe especificar a linha onde a expressão ou cadeia será apresentada no ecrã. O número da linha pode ser especificado como uma expressão. Tenha em atenção que o número da linha não se destina ao ecrã inteiro, mas à área imediatamente a seguir ao comando/programa. Este comando permite uma apresentação de dados semelhante a um painel em que o valor de uma expressão ou de uma leitura de sensor é atualizado na mesma linha. DispAte Disp podem ser utilizados no mesmo programa. Nota: o número máximo está definido para 8, uma vez que esse número corresponde a um ecrã cheio de linhas no ecrã da unidade portátil - desde que as linhas não contenham expressões matemáticas 2D. O número exato de linhas depende do conteúdo da informação apresentada.
|
Exemplo
Exemplos ilustrativos:
|
Condições de erro:
|
Mensagem de erro |
Descrição |
|---|---|
|
O número de linha DispAt deve situar-se entre 1 e 8 |
A expressão avalia o número de linha fora do intervalo 1-8 (inclusive) |
|
Poucos argumentos |
A função ou o comando não tem um ou mais argumentos. |
|
Nenhum argumento |
Igual à caixa de diálogo atual 'erro de sintaxe' |
|
Demasiados argumentos |
Limitar argumento. Mesmo erro que Disp. |
|
Tipo de dados inválido |
O primeiro argumento tem de ser um número. |
|
Nulo: DispAt nulo |
O erro de tipo de dados "Olá mundo" é projetado para o nulo (se o callback estiver definido) |
|
Operador de conversão: DispAt 2_ft @> _m, "Olá mundo" |
CAS: O erro de tipo de dados é projetado (se o callback estiver definido) Numérico: A conversão será avaliada e, se o resultado for um argumento válido, DispAt imprime a cadeia na linha de resultados. |
|
Catálogo > |
|
|
Lista 4DMS Matriz 4DMS Nota: Pode introduzir este operador através da escrita de @>DMS no teclado do computador. Interpreta o argumento como um ângulo e mostra o número DMS equivalente (DDDDDD ¡MM ' SS.ss ''). Consulte ¡, ', '' (aqui) para o formato DMS (grau, minutos, segundos). Nota: 4DMS converterá de radianos para graus quando utilizado em modo de radianos. Se a entrada for seguida por um símbolo de grau ¡, não ocorrerá nenhuma conversão. Pode utilizar o 4DMS apenas no fim de uma linha de entrada. |
No modo de ângulo Graus:
|
|
Catálogo > |
|
|
domain(Expr1, Var)Þexpressão Devolve o domínio de Expr1 em relação à Var. domain() pode ser utilizado para examinar domínios e funções. Está limitado ao domínio real e finito. Esta funcionalidade tem limitações devido a deficiências de simplificação algébrica computacional e a algoritmos de resolução. Certas funções não podem ser utilizadas como argumentos para domain(), independentemente de aparecerem explicitamente ou em variáveis e funções definidas pelo utilizador. No exemplo seguinte, a expressão não pode ser simplificada porque ‰() é uma função não permitida.
|
|
|
Catálogo > |
|
|
dominantTerm(Expr1, Var [, Ponto])Þexpressão dominantTerm(Expr1, Var [, Ponto]) | Var>Ponto Þexpressão dominantTerm(Expr1, Var [, Ponto]) Var<Ponto Þexpressão Devolve o termo dominante de uma representação da série de potência deExpr1 aberta sobre Ponto. O termo dominante é aquele cuja magnitude cresce mais rapidamente junto a Var = Ponto. A potência resultante de (Var N Ponto) pode ter um expoente fraccionário e/ou negativo. O coeficiente desta potência pode incluir logaritmos de (Var N Ponto) e outras funções de Var que são dominadas por todas as potências de (Var N Ponto) com o mesmo sinal de expoente. O Ponto predefine-se para 0. O Ponto pode ser ˆ ou Nˆ, nestes casos, o termo dominante será o termo com o expoente maior de Var em vez do expoente menor de Var. dominantTerm(…) devolve “dominantTerm(…)” se não for capaz de determinar essa representação, como para singularidades essenciais, como, por exemplo, sin(1/z) a z=0, eN1/z a z=0, ou ez a z = ˆ ou Nˆ. Se a série ou um das derivadas tiver uma descontinuidade em Ponto, o resultado contém provavelmente subexpressões do sinal(…) ou abs(…) da forma para uma variável de expansão real ou (-1)floor(…ângulo(…)…)para uma variável de expansão complexa, que é uma que termina com “_”. Se quiser utilizar o termo dominante apenas para os valores num lado de Ponto, adicione ao dominantTerm(...), um valor adequado de “| Var > Ponto”, “| Var < Ponto”, “| “Var | Ponto” ou “Var { Ponto” para obter um resultado mais simples. dominantTerm() distribui-se pelas listas e matrizes do 1º argumento. dominantTerm() é útil quando quiser saber a expressão mais simples possível que é assimptótica para outra expressão como Var " Ponto. dominantTerm() é também útil quando não for óbvio qual é o grau do primeiro termo não zero de uma série, e não quiser descobrir iterativamente de forma interactiva ou através de um ciclo do programa. Nota: Consulte também série(), aqui. |
|
|
Catálogo > |
|
|
dotP(Lista1, Lista2) Þexpressão Devolve o produto do “ponto” de duas listas. |
|
|
dotP(Vector1, Vector2) Þexpressão Devolve o produto do “ponto” de dois vectores. Ambos têm de ser vectores da linha ou da coluna. |
|