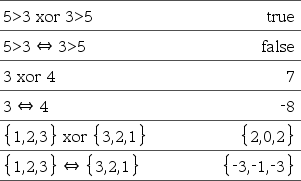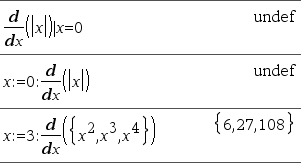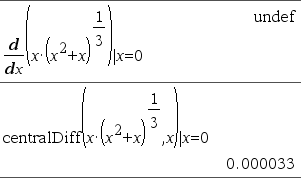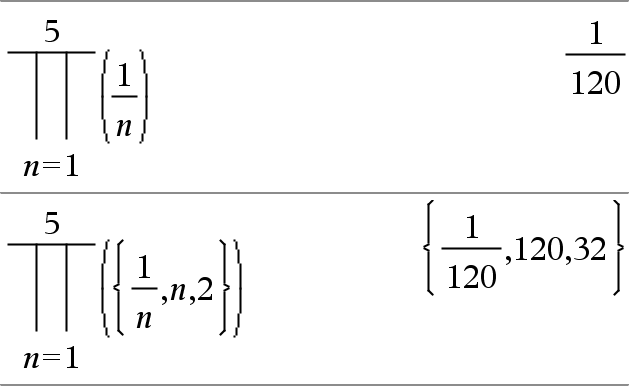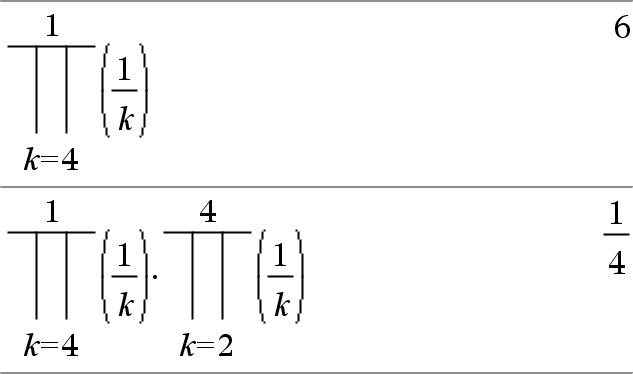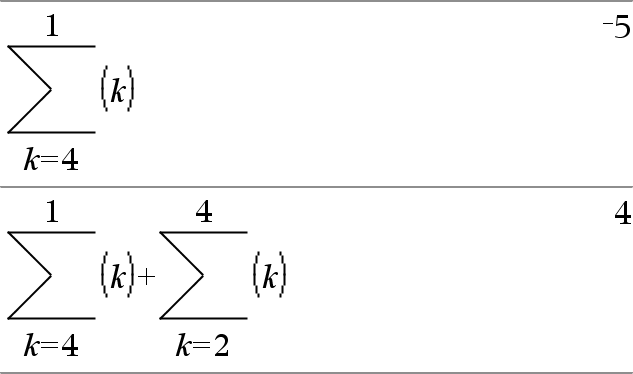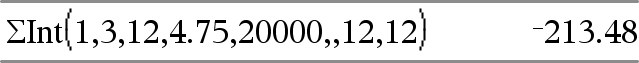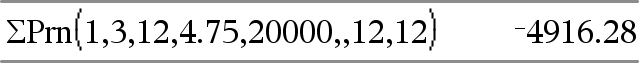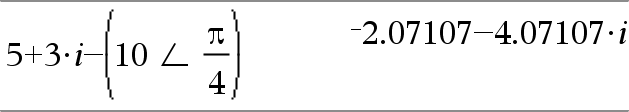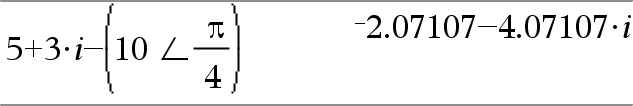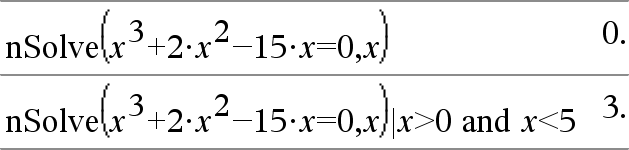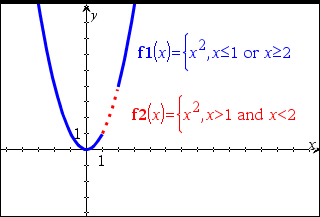|
+-tast |
|
|
Værdi1 + Værdi2Þværdi Returnerer summen af de to argumenter. |
|
|
Liste1 + Liste2Þliste Matrix1 + Matrix2Þmatrix Returnerer en liste (eller matrix), der indeholder summerne af tilsvarende elementer i Liste1 og Liste2 (eller Matrix1 og Matrix2). Argumenternes dimensioner må være ens. |
|
|
Tal + Liste1Þliste Liste1 + TalÞliste Returnerer en liste med summerne af Tal og hvert element i Liste1. |
|
|
Tal + Matrix1Þmatrix Matrix1 + TalÞmatrix Returnerer en matrix med Tal adderet til hvert element på diagonalen af Matrix1. Matrix1 skal være kvadratisk. Bemærk: Anvend .+ (punktum plus) til at addere et udtryk til hvert element. |
|
|
--tast |
|
|
Værdi1NVærdi2Þværdi Returnerer Værdi1 minus Værdi2. |
|
|
Liste1NListe2Þliste Matrix1NMatrix2Þmatrix Subtraherer hvert element i Liste2 (eller Matrix1) fra det tilsvarende element i Liste1 (eller Matrix1), og returnerer resultaterne. Argumenternes dimensioner må være ens. |
|
|
Tal NListe1Þliste Liste1NTalÞliste Subtraherer hver Liste1-element fra Tal eller subtraherer Tal fra hvert Liste1-element og returnerer en liste med resultaterne. |
|
|
Tal NMatrix1Þmatrix Matrix1NTalÞmatrix Tal N Matrix1 returnerer en matrix med Tal gange identitetsmatricen minus Matrix1. Matrix1 skal være kvadratisk. Matrix1 N Tal returnerer en matrix på Tal gange identitetsmatricen subtraheret fra Matrix1. Matrix1 skal være kvadratisk. Bemærk: Anvend .N (punktum minus) til at subtrahere et udtryk fra hvert element. |
|
|
r-tast |
|
|
Værdi1·Værdi2Þværdi Returnerer produktet af de to argumenter. |
|
|
Liste1·Liste2Þliste Returnerer en liste med produkterne af de tilsvarende elementer i Liste1 og Liste2. Listernes dimensioner må være ens. |
|
|
Matrix1·Matrix2Þmatrix Returnerer matrixproduktet af Matrix1 og Matrix2. Antallet af kolonner i Matrix1 skal være lig med antallet af rækker i Matrix2. |
|
|
Tal ·Liste1Þliste Liste1·TalÞliste Returnerer en liste med produkterne af Tal og hvert element i Liste1. |
|
|
Tal ·Matrix1Þmatrix Matrix1·TalÞmatrix Returnerer en matrix med produkterne af Tal og hvert element i Matrix1. Bemærk: Anvend .·(punktum gangetegn) til at gange et udtryk med hvert element. |
|
|
p-tast |
|
|
Værdi1à Værdi2Þværdi Returnerer kvotienten af Værdi1 divideret med Værdi2. Bemærk: Se også Brøkskabelon, her. |
|
|
Liste1 à Liste2Þliste Returnerer en liste med kvotienterne af Liste1 divideret medListe2. Listernes dimensioner må være ens. |
|
|
Tal àListe1Þliste Liste1àTalÞliste Returnerer en liste med kvotienterne af Tal divideret med Liste1 ellerListe1 divideret med Tal. |
|
|
TalàMatrix1Þmatrix Matrix1àTalÞmatrix Returnerer en matrix med kvotienterne af Matrix1àTal. Bemærk: Anvend . / (punktum divisionstegn) til at dividere et udtryk med hvert element. |
|
|
l-tast |
|
|
Værdi1 ^ Værdi2 Þ værdi Liste1 ^ Liste2 Þ liste Returnerer det første argument opløftet til potensen af det andet argument. Bemærk: Se også Eksponentskabelon, her. Ved en liste, returneres elementerne i Liste1 opløftet til potensen af de tilsvarende elementer i Liste2. I det reelle domæne anvender brøkpotenser, der har reducerede eksponenter med ulige nævnere, den reelle gren, i stedet for den principale gren i kompleks tilstand. |
|
|
Tal ^ Liste1Þliste Returnerer Tal opløftet til potensen af elementerne i Liste1. |
|
|
Liste1 ^ TalÞliste Returnerer elementerne i Liste1 opløftet til potensen af Tal. |
|
|
kvadratMatrix1 ^ heltalÞmatrix Returnerer kvadratMatrix1 opløftet til heltalspotensen. kvadratMatrix1 skal være en kvadratisk matrix. Hvis heltal = L1, beregnes den inverse matrix. Hvis heltal < L1, beregnes den inverse matrix til en passende positiv potens. |
|
|
q-tast |
|
|
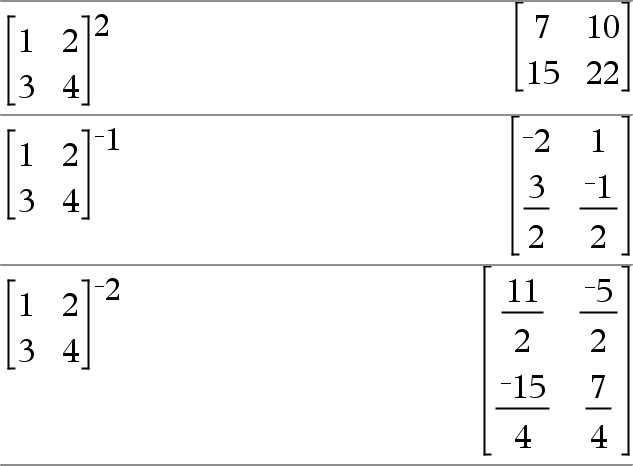
Værdi12 Þ værdi Returnerer kvadratet af argumentet. Liste12Þliste Returnerer en liste med kvadraterne på elementerne i Liste1. kvadratMatrix12 Þmatrix Returnerer matrix i anden potens af kvadratMatrix1. Dette er ikke det samme som at beregne kvadratet på hvert element. Brug .^2 til at beregne kvadratet på hvert element. |

|
|
^+-taster |
|
|
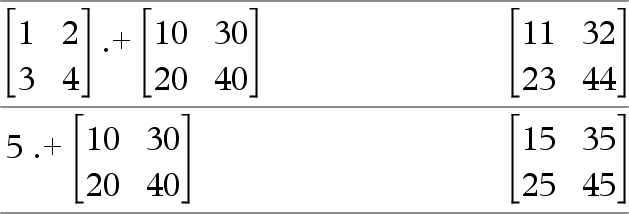
Matrix1 .+ Matrix2 Þ matrix Tal .+ Matrix1 Þ matrix Matrix1 .+ Matrix2 returnerer en matrix, der er summen af hvert par tilsvarende elementer i Matrix1 og Matrix2. Tal .+ Matrix1 returnerer en matrix, der er summen af Tal og hvert element i Matrix1. |
|
|
^--taster |
|
|
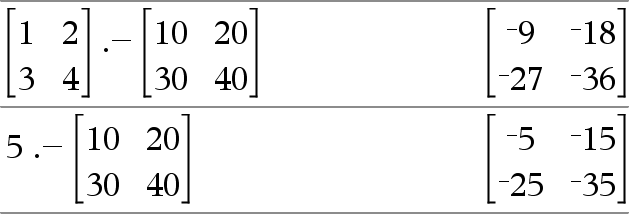
Matrix1 .NMatrix2 Þ matrix Tal .NMatrix1 Þ matrix Matrix1 .NMatrix2 returnerer en matrix, der er differensen mellem hvert par af tilsvarende elementer i Matrix1 og Matrix2. Tal .NMatrix1 returnerer en matrix, der er der er differensen af Tal og hvert element i Matrix1. |
|
|
^r-taster |
|
|
Matrix1 .· Matrix2 Þ matrix Tal .·Matrix1 Þ matrix Matrix1 .· Matrix2 returnerer en matrix, der er produktet af hvert par tilsvarende elementer i Matrix1 og Matrix2. Tal .· Matrix1 returnerer en matrix med produkterne af Tal og hvert element i Matrix1. |
|
|
^p-taster |
|
|
Matrix1 . / Matrix2 Þ matrix Tal . / Matrix1 Þ matrix Matrix1 ./ Matrix2 returnerer en matrix, der er kvotient af hvert par af tilsvarende elementer i Matrix1 og Matrix2. Tal ./ Matrix1 returnerer en matrix, der er kvotienten af Tal og hvert element i Matrix1. |
|
|
^l-taster |
|
|
Matrix1^Matrix2Þmatrix Tal.^Matrix1Þmatrix Matrix1 .^ Matrix2 returnerer en matrix, hvor hvert element i Matrix2 er eksponent til det tilsvarende element i Matrix1. Tal .^ Matrix1 returnerer en matrix, hvor hvert element i Matrix1 er eksponenten til Tal. |
|
|
v-tast |
|
|
LVærdi1 Þ værdi LListe1 Þ liste LMatrix1 Þ matrix Returnerer negationen til argumentet. Ved en liste eller matrix, returneres alle elementer negeret. Hvis argumentet er et binært eller hexadecimalt heltal, giver negationen 2's komplement. |
I binær tilstand: Vigtigt: Tallet nul, ikke bogstavet O
Du kan se hele resultatet ved at trykke på 5 og derefter bruge 7 og 8 til at bevæge markøren. |
|
/k-taster |
|
|
Værdi1 % Þ værdi Liste1 % Þ liste Matrix1 % Þ matrix Returnerer For en liste eller matrix returneres en liste eller matrix med hvert element divideret med 100. |
Bemærk: Sådan gennemtvinges et tilnærmet resultat, Håndholdt: Tryk på / ·.
|
|
=-tast |
|
|
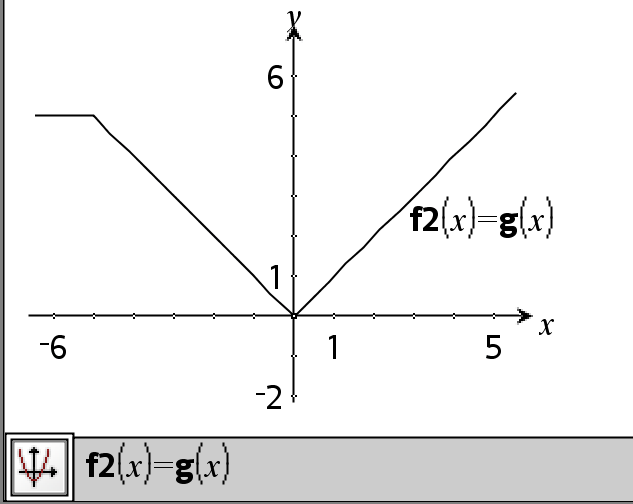
Udtr1 = Udtr2ÞBoolsk udtryk Liste1 = Liste2Þ Boolsk liste Matrix1 = Matrix2Þ Boolsk matrix Returnerer sand, hvis Udtr1 bestemmes til at være lig med Udtr2. Returnerer false, hvis Udtr1 bestemmes til at være forskelligt fra Udtr2. Alt andet returnerer en reduceret form af ligningen. For lister og matricer returneres sammenligninger element for element. Bemærk indtastning af eksemplet: For instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning. |
Eksempelfunktion, der anvender matematiske testsymboler: =, ƒ, <, {, >, |
Tegnet resultat af grafen g(x)
|
|
/=-taster |
|
|
Udtr1 ƒ Udtr2 Þ Boolsk udtryk Liste1 ƒ Liste2 Þ Boolsk liste Matrix1 ƒ Matrix2 Þ Boolsk matrix Returnerer true, hvis Udtr1 bestemmes til at være forskellig fra Udtr2. Returnerer false, hvis Udtr1 bestemmes til at være lig med Udtr2. Alt andet returnerer en reduceret form af uligheden. For lister og matricer returneres sammenligninger element for element. Bemærk: Du kan indsætte denne operator fra tastaturet ved at skrive /= |
Se “=” (lig med)-eksemplet. |
|
/= taster |
|
|
Udtr1 < Udtr2 Þ Boolsk udtryk Liste1 < Liste2 Þ Boolsk liste Matrix1 < Matrix2 Þ Boolsk matrix Returnerer true, hvis Udtr1 bestemmes til at være mindre end Udtr2. Returnerer false, hvis Udtr1 bestemmes til at være større end Udtr2. Alt andet returnerer en reduceret form af ligningen. For lister og matricer returneres sammenligninger element for element. |
Se “=” (lig med)-eksemplet. |
|
/= taster |
|
|
Udtr1 { Udtr2 Þ Boolsk udtryk Liste1 { Liste2 Þ Boolsk liste Matrix1 { Matrix2 Þ Boolsk matrix Returnerer true, hvis Udtr1 bestemmes til at være mindre end eller lig med Udtr2. Returnerer false, hvis Udtr1 bestemmes til at være større end eller lig med Udtr2. Alt andet returnerer en reduceret form af uligheden. For lister og matricer returneres sammenligninger element for element. Bemærk: Du kan indsætte denne operator fra tastaturet ved at skrive <= |
Se “=” (lig med)-eksemplet. |
|
/= taster |
|
|
Udtr1 > Udtr2 Þ Boolsk udtryk Liste1 > Liste2 Þ Boolsk liste Matrix1 > Matrix2 Þ Boolsk matrix Returnerer true, hvis Udtr1 bestemmes til at være større end Udtr2. Returnerer false, hvis Udtr1 bestemmes til at være mindre end eller lig med Udtr2. Alt andet returnerer en reduceret form af uligheden. For lister og matricer returneres sammenligninger element for element. |
Se “=” (lig med)-eksemplet. |
|
/= taster |
|
|
Udtr1 | Udtr2 Þ Boolsk udtryk Liste1 | Liste2 Þ Boolsk liste Matrix1 | Matrix2 Þ Boolsk matrix Returnerer true, hvis Udtr1 bestemmes til at være større end eller lig med Udtr2. Returnerer false, hvis Udtr1 bestemmes til at være mindre end Udtr2. Alt andet returnerer en reduceret form af uligheden. For lister og matricer returneres sammenligninger element for element. Bemærk: Du kan indsætte denne operator fra tastaturet ved at skrive >= |
Se “=” (lig med)-eksemplet. |
|
/=-taster |
|
|
BoolskUdtryk1 Þ BoolskUdtryk2 returnerer Boolsk udtryk BoolskListe1 Þ BoolskListe2 returnerer Boolsk liste BoolskMatrix1 Þ BoolskMatrix2 returnerer Boolsk matrix Heltal1 Þ Heltal2 returnerer Heltal
Beregner udtrykket For lister og matricer returneres sandhedsværdier element for element. Bemærk: Du kan indsætte denne operator fra tastaturet ved at skrive => |
|
|
/=-taster |
|
|
BoolskUdtryk1 Û BoolskUdtryk2 returnerer Boolsk udtryk BoolskListe1 Û BoolskListe2 returnerer Boolsk liste BoolskMatrix1 Û BoolskMatrix2 returnerer Boolsk matrix Heltal1 Û Heltal2 returnerer Heltal
Returnerer negationen af en logisk XOR Boolsk operation anvendt på de to argumenter. Returnerer true eller false eller en forenklet form af ligningen. For lister og matricer returneres sandhedsværdierne element for element. Bemærk: Du kan indsætte denne operator fra tastaturet ved at skrive <=> |
|
|
º-tast |
|
|
Værdi1! Þ værdi Liste1! Þ liste Matrix1! Þ matrix Returnerer fakultetværdien af argumentet. For en liste eller matrix returneres en liste eller matrix af elementerne. |
|
|
/k-taster |
|
|
Streng1 & Streng2 Þ streng Returnerer en tekststreng, der er Streng2 adderet til Streng1. |
|
|
Katalog > |
|
|
d(Udtr1, Var[,Orden]) | Var=VærdiÞværdi d(Udtr1, Var[,Orden])Þværdi d(1, Var[,Orden])Þliste d(Matrix1,Var[,Orden])Þmatrix Med undtagelse af, når første syntaks anvendes, skal den numeriske værdi lagres i en variabel Var, før der beregnes på d(). Se eksemplerne. d() kan anvendes til beregning af differentialkvotienter af første og anden orden numerisk i et punkt ved hjælp af automatiske differentiationsmetoder. Hvis Orden medtages, skal den være =1 eller 2. Standardindstillingen er 1. Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive Bemærk: Se også Differentialkvotient af første orden, her eller Differentialkvotient af anden orden, her. |
|
|
Bemærk: Algoritmen d() har en begrænsning: Den arbejder sig rekursivt gennem det uforkortede udtryk og beregner den numeriske værdi af differentialkvotienten af første orden (og anden, hvis relevant) af hvert deludtryk, hvilket kan føre til et utilsigtet resultat. Betragt eksemplet til højre. Differentialkvotienten af første orden af x·(x^2+x)^(1/3) at x=0 er lig med 0. Man da differentialkvotienten af underudtrykket (x^2+x)^(1/3) ikke er defineret i x=0, og denne værdi anvendes til at beregne differentialkvotienten af det samlede udtryk, rapporterer d() resultatet som udefineret og viser en advarsel. Hvis du rammer denne begrænsning, skal du kontrollere løsningen grafisk. Du kan også prøve med centralDiff(). |
|
|
Katalog > |
|
|
‰(Udtr1, Var, Nedre, Øvre) Þ værdi Returnerer integralet af Udtr1 med hensyn til variablen var fra Nedre til Øvre. Kan anvendes til at beregne det bestemte integral numerisk med samme metode som nInt(). Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive integral(...). Bemærk: Se også nInt(), her, og Bestemt integralskabelon, her. |
|
|
/q-taster |
|
|
‡ (Værdi1)Þværdi ‡ (Liste1)Þliste Returnerer kvadratroden af argumentet. For en liste returneres kvadratrødderne af alle elementer i Liste1. Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive sqrt(...) Bemærk: Se også Kvadratrodsskabelon, her. |
|
|
Katalog > |
|
|
P(Udtr1, Var, Lav, Høj)Þudtryk Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive prodSeq(...). Beregner Udtryk1 for hver værdi af Var fra Lav til Høj og returnerer produktet af resultaterne. Bemærk: Se også Produktskabelon (P), her. |
|
|
P(Udtr1, Var, Lav, LavN1)Þ1 P(Udtr1, Var, Lav, Høj) Þ1/P(Udtr1, Var, Høj+1, LavN1) hvis Høj < LavN1
De anvendte produktformler stammer fra følgende reference: Ronald L. Graham, Donald E. Knuth og Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Katalog > |
|
|
G(Udtr1, Var, Lav, Høj)Þudtryk Bemærk: Du kan indsætte denne funktion fra computerens tastatur ved at skrive sumSeq(...). Beregner Udtr1 for hver værdi af Var fra Lav til Høj og returnerer summen af resultaterne. Bemærk: Se også Sumskabelon, her. |
|
|
G(Udtr1, Var, Lav, LavN1) Þ 0 G(Udtr1, Var, Lav, Høj) Þ LG(Udtr1, Var, Høj+1, LavN1) hvis Høj < LavN1
De anvendte summationsformler stammer fra følgende reference: Ronald L. Graham, Donald E. Knuth og Oren Patashnik. Concrete Mathematics: A Foundation for Computer Science. Reading, Massachusetts: Addison-Wesley, 1994. |
|
|
Katalog > |
||||||||||
|
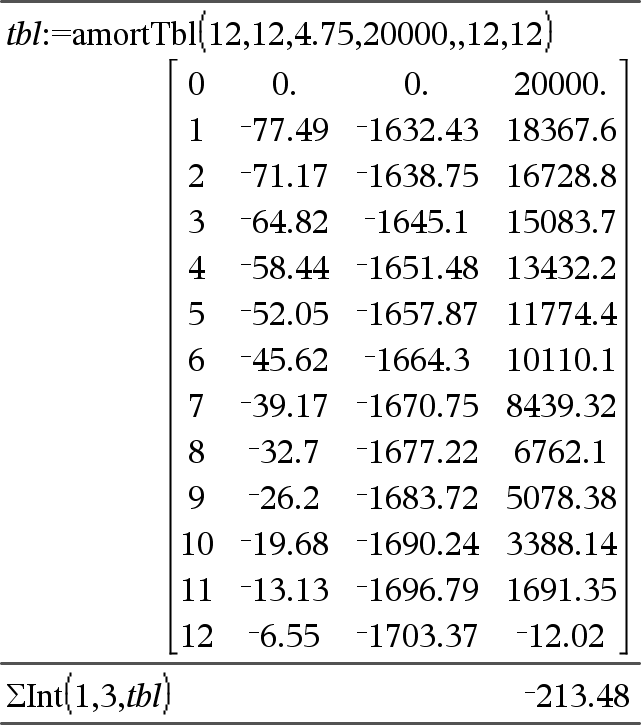
GInt(NPmt1, NPmt2, N, I, PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [afrundVærdi])Þværdi GInt(NPmt1,NPmt2,amortTabel)Þværdi Amortiseringsfunktion, der beregner summen af renter under en angivet række af betalinger. NPmt1 og NPmt2 definerer starten og slutningen af betalingsrækken. N, I, PV, Pmt, FV, PpY, CpY og PmtAt er beskrevet i tabellen over TVM-argumenter på her.
afrundVærdi angiver antallet af decimaler til afrunding. Standardværdi=2. GInt(NPmt1,NPmt2,amortTabel) beregner summen af renten baseret på amortiseringstabellen amortTabel. amortTabel-argumentet skal være en matrix i formen beskrevet under amortTbl(), her. Bemærk: Se også GPrn() nedenfor og Bal(), her. |
|
|
Katalog > |
||||||||||
|
GPrn(NPmt1, NPmt2, N, I, PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [afrundVærdi])Þværdi GPrn(NPmt1,NPmt2,amortTabel)Þværdi Amortiseringsfunktion, der beregner summen af afdraget under en angivet række af betalinger. NPmt1 og NPmt2 definerer starten og slutningen af betalingsrækken. N, I, PV, Pmt, FV, PpY, CpY og PmtAt er beskrevet i tabellen over TVM-argumenter på her.
afrundVærdi angiver antallet af decimaler til afrunding. Standardværdi=2. GPrn(NPmt1,NPmt2,amortTabel) beregner summen af afdrag på hovedstolen baseret på amortiseringstabellen amortTabel. amortTabel-argumentet skal være en matrix i formen beskrevet under amortTbl(), her. Bemærk: Se også GInt() ovenfor og Bal(), her. |
|
|
/k-taster |
|
|
# varNavnestreng Kalder variablen, hvis navn er varNavnestreng. Dermed kan du anvende strenge til at oprette variabelnavne fra en funktion. |
Opretter eller kalder variablen xyz.
Returnerer værdien af variablen (r), hvis navn er lagret i variablen s1. |
|
i-tast |
|
|
mantisseEeksponent Indtaster et tal i videnskabelig notation. Tallet fortolkes som mantisse × 10eksponent. Tip: Hvis du vil indtaste en 10. potens uden at give et decimalværdiresultat, skal du bruge 10^heltal. Bemærk: Du kan indsætte denne operator fra computerens tastatur ved at skrive @E. Skriv for eksempel 2.3@E4 for at indtaste 2.3E4. |
|
|
1-tast |
|
|
Udtr1gÞudtryk Udtr1gÞudtryk Liste1gÞliste Matrix1gÞmatrix Denne funktion giver mulighed for at angive en vinkel i nygrader, mens programmet er i vinkeltilstanden Grader eller Radianer. I vinkeltilstanden Radian ganges Udtr1 med p/200. I vinkeltilstanden Grader ganges Udtr1 med g/100. I vinkeltilstanden Nygrader returneres Udtr1 uændret. Bemærk: Du kan indsætte dette symbol fra computerens tastatur ved at skrive @g. |
I vinkeltilstanden Grader, Nygrader eller Radianer:
|
|
1-tast |
|
|
Værdi1RÞværdi Liste1RÞliste Matrix1RÞmatrix Denne funktion giver mulighed for at angive en vinkel i radianer, mens programmet er i vinkeltilstanden Grader eller Nygrader. I vinkeltilstanden Grader ganges argumentet med 180/p. I vinkeltilstanden Radian, returneres argument uændret. I vinkeltilstanden Nygrader ganges argumentet med 200/p. Tip: Anvend R, hvis du vil fremtvinge radianer i en funktionsdefinition uanset den aktuelle tilstand, når funktionen anvendes. Bemærk: Du kan indsætte dette symbol fra computerens tastatur ved at skrive @r. |
I vinkeltilstanden Grader, Nygrader eller Radianer:
|
|
1-tast |
|
|
Værdi1¡Þværdi Liste1¡Þliste Matrix1¡Þmatrix Denne funktion giver mulighed for at angive en vinkel i grader, mens programmet er i vinkeltilstanden Nygrader eller Radianer. I vinkeltilstanden Radian ganges argumentet med p/180. I vinkeltilstanden grader returneres argument uændret. I vinkeltilstanden Nygrader ganges argumentet med 10/9. Bemærk: Du kan indsætte dette symbol fra computerens tastatur ved at skrive @d. |
I vinkeltilstanden Grader, Nygrader eller Radianer:
I vinkeltilstanden Radianer: |
|
/k-taster |
|||||||
|
gg¡mm'ss.ss''Þudtryk ggEt positivt eller negativt tal mmEt ikke-negativt tal ss.ssEt ikke-negativt tal Returnerer gg+(mm/60)+(ss.ss/3600). Med denne indtastning i 60‑talsformat kan du:
Bemærk: Efterfølg ss.ss med to apostroffer (''), ikke et citationstegn ("). |
I vinkeltilstanden Grader:
|
|
/k-taster |
|
|
[Radius,±q_Vinkel ]Þvektor [Radius,±q_Vinkel,Z_Koordinat ]Þvektor [Radius,±q_Vinkel,±q_Vinkel ]Þvektor Returnerer koordinater som en vektor afhængigt af tilstandsindstillingen for vektorformat: rektangulær, cylindrisk eller sfærisk. Bemærk: Du kan indsætte dette symbol fra computerens tastatur ved at skrive @<. |
I vinkeltilstanden Radian og vektorformatet indstillet til: rektangulær
cylindrisk
sfærisk
|
|
(Størrelse ± Vinkel)ÞkompleksVærdi Indtaster en kompleks værdi i den polære form (r±q). Vinkel fortolkes efter den aktuelle indstilling af vinkeltilstand. |
I vinkeltilstanden radian og rektangulært komplekst format:
|
|
Se |“Tomme (ugyldige) elementer” her, . |
|
|
|
|
|
/_-taster |
|
|
Variabel_ Når Variabel ikke har nogen værdi, behandles den, som om den repræsenterer et komplekst tal. Uden_ behandles variablen som reel. Hvis Variabel har en værdi, ignoreres _, og Variabel bevarer sin oprindelige datatype. |
Det antages, at z er udefineret:
|
|
Katalog > |
|
|
10^ (Værdi1)Þværdi 10^ (Liste1)Þliste Returnerer 10 opløftet til potensen af argumentet. I en liste returneres 10 opløftet til potensen af elementerne i Liste1. |
|
|
10^(kvadratMatrix1)Þkvadratmatrix Returnerer 10 opløftet til potensen af kvadratMatrix1. Dette er ikke det samme som at beregne 10 opløftet til potensen af hvert element. Oplysninger om beregningsmetoden findes i cos(). KvadratMatrix1 skal være diagonaliserbar. Resultatet indeholder altid tal med flydende decimaler. |
|
|
Katalog > |
|
|
Værdi1 ^/Þværdi Liste1 ^/Þliste Returnerer den reciprokke værdi af argumentet. For en liste returneres de reciprokke værdier af elementerne i Liste1. |
|
|
kvadratMatrix1 ^/ÞkvadratMatrix Returnerer den inverse værdi af kvadratMatrix1. kvadratMatrix1 skal være en ikke-singulær kvadratisk matrix. |
|
|
/k-taster |
||||||||||
|
Udtryk | BoolskUdtryk1 [ Udtryk | BoolskUdtryk1 [ (“|”)-betingelses-tegnet fungerer som en binær operator. Argumentet til venstre for | er et udtryk. Argumentet til højre for | angiver en eller flere betingelser, der skal tages hensyn til i reduktionen af udtrykket. Hvis der er flere betingelser efter |, skal de samles med en logisk “ Betingelses-operatoren bruges på tre grundlæggende måder:
|
|
|||||||||
|
Substitutioner er i form af en ligning, som x=3 eller y=sin(x). For at være så effektiv som muligt skal venstre side af betingelsen være en simpel variabel. Udtryk | Variabel = værdi vil substituere værdi for enhver forekomst af Variabel i Udtryk. |
|
|||||||||
|
Intervalafgrænsning antager form af en eller flere uligheder samlet af logiske “ |
|
|||||||||
|
Udelukkelser benytter “forskellig fra”-kommandoen (/= eller ƒ) til at udelukke en specifik værdi fra reduktionen. |
|
/h-tast |
|
|
Værdi &Var Liste&Var Matrix&Var Udtr&Funktion(Param1,...) List&Funktion(Param1,...) Matrix&Funktion(Param1,...) Hvis variablen Var ikke findes, oprettes Var og initialiseres til Værdi, Liste eller Matrix. Hvis Var findes i forvejen og ikke er låst eller beskyttet, erstattes dens indhold med Værdi, Liste eller Matrix. Bemærk: Du kan indsætte denne operator fra tastaturet ved at skrive =: som en genvej. Skriv for eksempel pi/4 =: myvar. |
|
|
/t -taster |
|
|
Var := Værdi Var := Liste Var := Matrix Funktion(Param1,...) := Udtr Funktion(Param1,...) := Liste Funktion(Param1,...) := Matrix Hvis variablen Var ikke findes, oprettes Var og initialiseres til Værdi, Liste eller Matrix. Hvis Var findes i forvejen og ikke er låst eller beskyttet, erstattes dens indhold med Værdi, Liste eller Matrix. |
|
|
/k-taster |
|
|
© [tekst] © behandler tekst som en kommentarlinje, så du kan skrive kommentarer til funktioner og programmer, du opretter. © kan være i starten eller overalt i linjen. Alt til højre for © til linjens slutning er kommentaren. Bemærk indtastning af eksemplet: For instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning. |
|
|
0B-taster, 0H-taster |
|
|
0b binærtTal 0h hexadecimaltTal Betegner henholdsvis binært eller hexadecimalt tal. For at indtaste et binært eller hexadecimalt tal skal du indtaste præfikset 0b eller 0h uanset talsystemet. Uden præfiks behandles tallet som decimaltal (10 talssystem). Resultatet vises i den valgte tilstand for talsystem. |
I decimal tilstand:
I binær tilstand:
I hexadecimal tilstand:
|















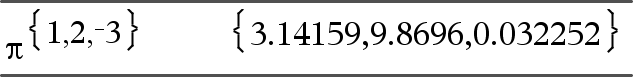

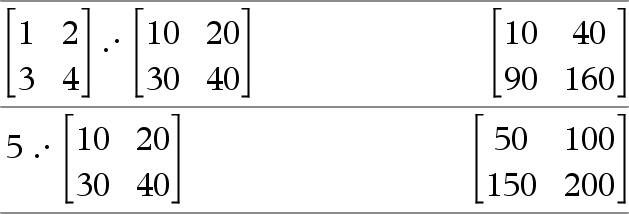
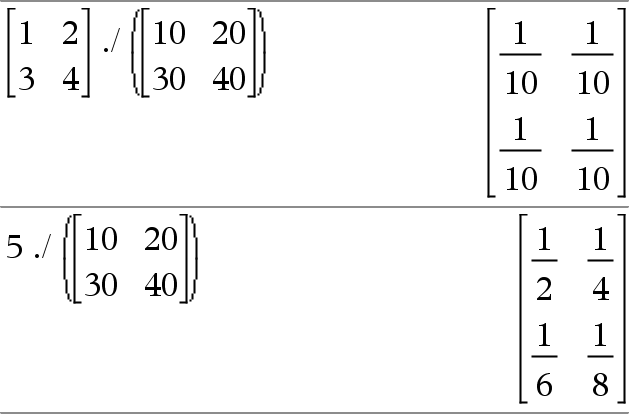
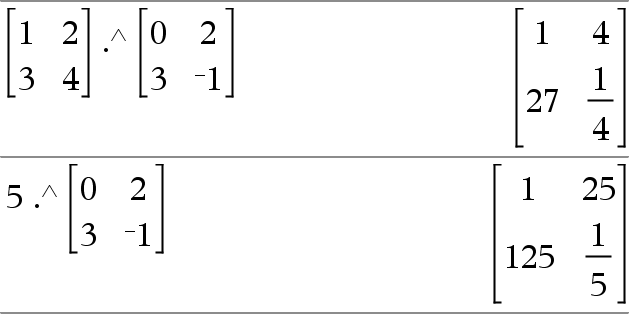
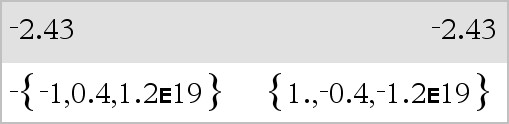
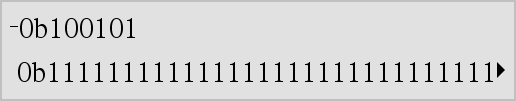
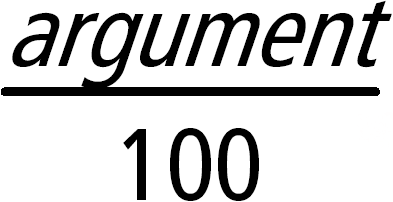
 .
.