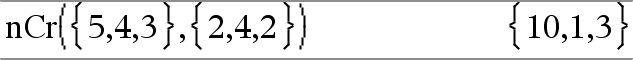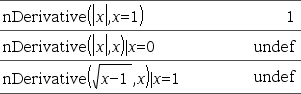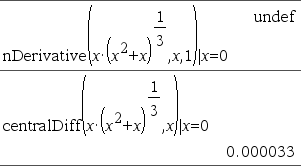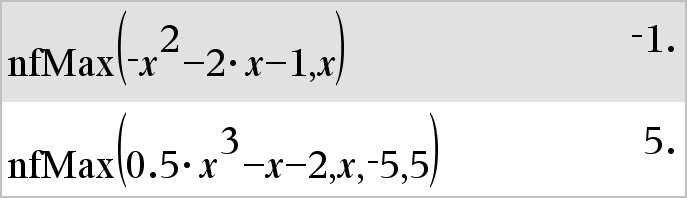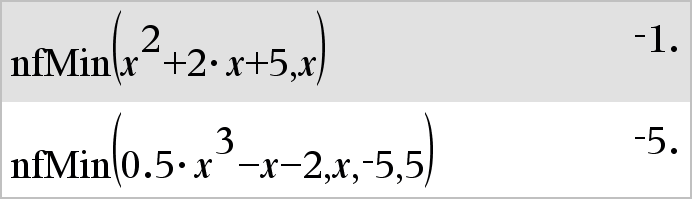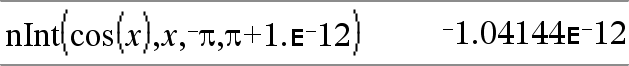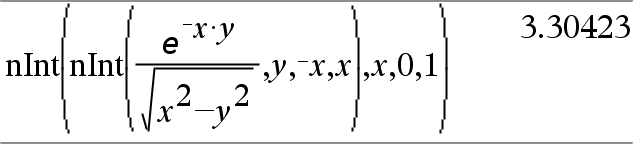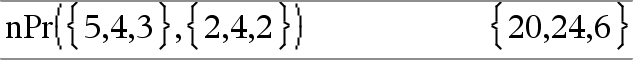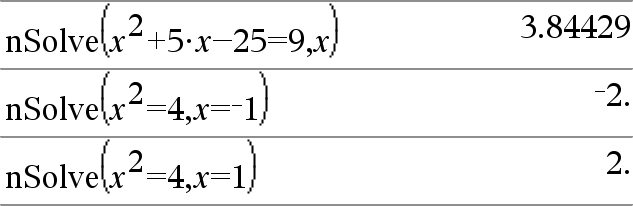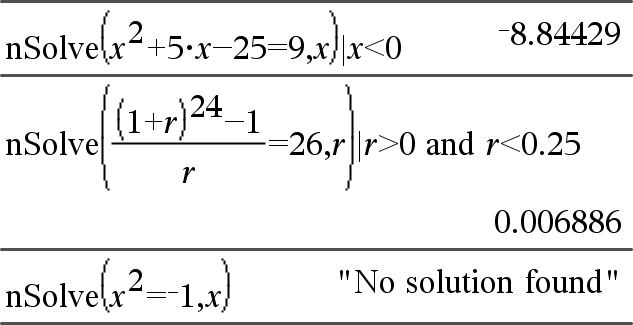|
Katalog > |
|
|
nCr(Værdi1, Værdi2)Þudtryk For heltal Værdi1 og Værdi2 med Værdi1 | Værdi2 | 0, nCr() er antallet af kombinationer af Værdi1 ting taget Værdi2 ad gangen. (Dette kendes også som en binomial koefficient). nCr(Tal, 0)Þ1 nCr(Tal, negHeltal)Þ0
(TalNposHeltal+1)/posHeltal!
|
|
|
nCr(Liste1, Liste2)Þliste Returnerer en liste med kombinationer baseret på de sammenhørende elementpar i de to lister. Argumenterne skal være lister af samme størrelse. |
|
|
nCr(Matrix1, Matrix2)Þmatrix Returnerer en matrix af kombinationer baseret på de sammenhørende elementpar i de to matricer. Argumenterne skal være matricer af samme størrelse. |
|
|
Katalog > |
|
|
Returnerer den numeriske differentialkvotient udregnet med en automatisk differentiationsmetode. Når Værdi er angivet, tilsidesætter den alle forudgående variabeltildelinger og alle nuværende “|” substitutioner for variablen. Hvis variablen Var ikke indeholder en numerisk værdi, skal du angive Værdi. Differentialkvotientens orden skal være 1 eller 2. |
|
|
Betragt eksemplet til højre. Differentialkvotienten af første orden af x·(x^2+x)^(1/3) i x=0 er lig med 0. Men da differentialkvotienten af underudtrykket (x^2+x)^(1/3) ikke er defineret i x=0, og denne værdi anvendes til at beregne differentialkvotienten af det samlede udtryk, rapporterer nDerivative() resultatet som udefineret og viser en advarsel. Hvis du rammer denne begrænsning, skal du kontrollere løsningen grafisk. Du kan også prøve med centralDiff(). |
|
|
Katalog > |
|
|
newList(antalElementer)Þliste Returnerer en liste med en dimension af antalElementer. Hvert element er nul. |
|
|
Katalog > |
|
|
newMat(antalRækker, antalKolonner)Þmatrix Returnerer en matrix med nulpunkter af dimensionen antalRækker gange antalKolonner. |
|
|
Katalog > |
|
|
nfMax(Udtr, Var)Þværdi nfMax(Udtr, Var, nedreGrænse)Þværdi nfMax(Udtr, Var, nedreGrænse, øvreGrænse)Þværdi nfMax(Udtr, Var) | nedreGrænse{Var{øvreGrænseÞværdi Returnerer mulig numerisk værdi for variablen Var, hvor det lokale maksimum for Udtr optræder. Hvis du opgiver nedreGrænse og øvreGrænse, søger funktionen i det lukkede interval [nedreGrænse,øvreGrænse] efter det lokale maksimum. |
|
|
Katalog > |
|
|
nfMin(Udtr, Var)Þværdi nfMin(Udtr, Var, nedreGrænse)Þværdi nfMin(Udtr, Var, nedreGrænse, øvreGrænse)Þværdi nfMin(Udtr, Var) | nedreGrænse{Var{øvreGrænseÞværdi Returnerer mulig numerisk værdi for variablen Var, hvor det lokale minimum for Udtr optræder. Hvis du opgiver nedreGrænse og øvreGrænse, søger funktionen i det lukkede interval [nedreGrænse,øvreGrænse] efter det lokale minimum. |
|
|
Katalog > |
|
|
nInt(Udtr1, Var, nedre, øvre)Þudtryk Hvis integranden Udtr1 ikke indeholder andre variable end Var, og hvis Nedre og Øvre er konstante, + ˆ eller - ˆ, så returnerer nInt() en tilnærmet værdi af ‰(Udtr1, Var, Nedre, Øvre). Denne tilnærmede værdi er et vægtet gennemsnit af nogle eksempelværdier af integranden i intervallet Nedre<Var<Øvre. |
|
|
Målet er seks betydende cifre. Algoritmen, der kan tilpasses, afsluttes hvis det virker sandsynligt, at målet er nået, eller når det virker usandsynligt, at ydeligere eksempler vil give en væsentlig forbedring. Der vises en advarsel (“Tvivl om nøjagtighed“) når målet ikke ser ud til at være nået. |
|
|
Indskyd flere nInt(), for at foretage numerisk integration i flere variable. Integrationsgrænser kan afhænge af integrationsvariable uden for dem. |
|
|
Katalog > |
|
|
nom(effektivRente,CpY)Þværdi Finansfunktion, der omregner den effektive årlige rente effektivRente til en nominel rente, hvor CpY er antallet af rentetilskrivninger per år. effektivRente skal være et reelt tal, og CpY skal være et reelt tal > 0. Bemærk: Se også eff(), her. |
|
|
/=-taster |
|
|
BoolskUdtryk1 BoolskListe1 BoolskMatrix1
Returnerer negationen af en logisk or operation anvendt på de to argumenter. Returnerer true eller false eller en forenklet form af ligningen. For lister og matricer returneres sandhedsværdierne element for element. |
|
|
Heltal1
Sammenligner to reelle heltal bit for bit med en nor operation. Internt konverteres begge heltal til 64-bit binære tal med fortegn. Når de tilsvarende bits sammenlignes, er resultatet 0, hvis begge bits er 1. Ellers er resultatet 1. Den returnerede værdi repræsenterer bit-resultaterne og vises i overensstemmelse med den valgte talsystemtilstand. Du kan indtaste heltallene i ethvert talsystem. Til binære eller hexadecimale indtastninger skal du som præfiks benytte henholdsvis 0b eller 0h. Uden præfiks behandles heltallene som decimaltal (10 talssystem) |
|
|
Katalog > |
|
|
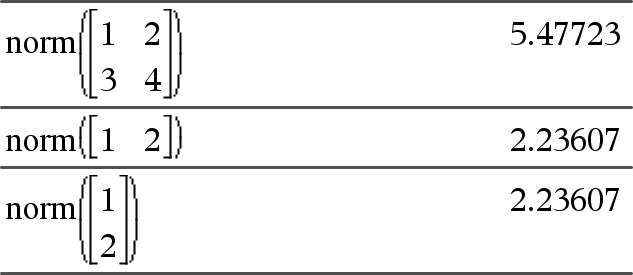
norm(Matrix)Þudtryk norm(Vektor)Þudtryk Returnerer Frobenius-normen. |
|
|
Katalog > |
|
|
normCdf(nedreGrænse,øvreGrænse[,m[,s]])Þtal hvis nedreGrænse og øvreGrænse er tal, liste hvis nedreGrænse og øvreGrænse er lister Beregner normalfordelingenssandsynligheden mellem nedreGrænse og øvreGrænse for de angivne m (standard=0) og s (standard=1). For P(X { øvreGrænse), sæt nedreGrænse= .9E999. |
|
|
Katalog > |
|
|
normPdf(XVærdi[,m,s])Þtal hvis XVærdi er et tal, liste hvis XVærdi er en liste Beregner tæthedsfunktionen for normalfordelingen i en angivet XVærdi for de angivne m og s. |
|
|
Katalog > |
|
|
not Boolsk udtr1ÞBoolsk udtryk Returnerer true eller false eller en forenklet form af argumentet. |
|
|
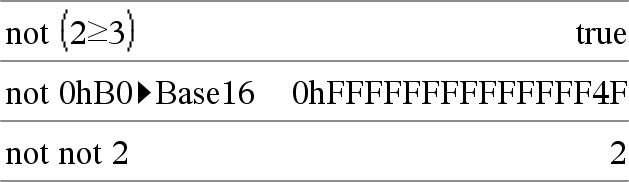
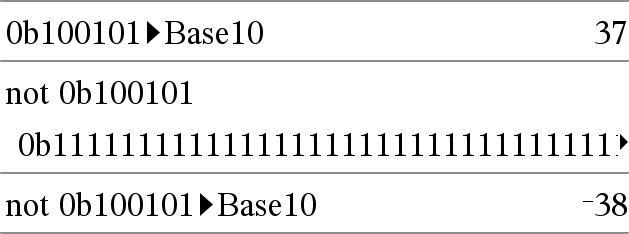
not Heltal1Þheltal Returnerer 1's komplement til et reelt heltal. Internt konverteres Heltal1 til et 64-bit binært tal med fortegn. Værdien af hver bit vendes (0 bliver 1, og omvendt) for 1's komplement. Resultatet vises i den valgte tilstand for talsystem. Du kan indtaste heltallet i ethvert talsystem. Til binære eller hexadecimale indtastninger skal du som præfiks benytte henholdsvis 0b eller 0h. Uden præfiks behandles heltallet som decimaltal (10-talssystem). Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær form med fortegn, anvendes en symmetrisk modulo-operation til at bringe værdien ind i det korrekte område. Yderligere oplysninger findes under 4Base2, her. |
I hexadecimal tilstand: Vigtigt: Tallet nul, ikke bogstavet O.
I binær tilstand:
Du kan se hele resultatet ved at trykke på 5 og derefter bruge 7 og 8 til at bevæge markøren. Bemærk: En binær indtastning kan have op til 64 cifre (præfikset 0b ikke medregnet). En hexadecimal indtastning kan have op til 16 cifre. |
|
Katalog > |
|
|
nPr(Værdi1, Værdi2)Þudtryk For heltal er Værdi1 og Værdi2 med Værdi1 | Værdi2 | 0, nPr() antallet af permutationer af Værdi1 ting taget Værdi2 ad gangen. nPr(Tal, 0)Þ1 nPr(Tal, negHeltal) Þ 1/((Tal+1)·(Tal+2)... (TalNnegHeltal)) nPr(Tal, posHeltal) Þ Tal·(TalN1)... (TalNposHeltal+1) nPr(Tal, ikke-Heltal) |
|
|
nPr(Liste1, Liste2) Þ liste Returnerer en liste med permutationer baseret på de sammenhørende elementpar i de to lister. Argumenterne skal være lister af samme størrelse. |
|
|
nPr(Matrix1, Matrix2)Þmatrix Returnerer en matrix med permutationer baseret på de sammenhørende elementpar i de to matricer. Argumenterne skal være matricer af samme størrelse. |
|
|
Katalog > |
|
|
npv(RenteSats,CFO,CFListe[,CFFrekv]) Finansfunktion, der beregner nettonutidsværdien. Summen af de aktuelle værdier for indkommende og udgående pengestrømme. Et positivt resultat for npv indikerer en profitabel investering. RenteSats er renten, som pengestrømmen skal reduceres med over en periode (pengenes pris). CF0 er startpengestrømmen på tidspunkt 0. Den skal være et reelt tal. CFListe er en liste over pengestrømsbeløb efter startpengestrømmen CF0. CFFrekv er en liste, hvor hvert element angiver hyppighedsfrekvensen for et grupperet (fortløbende) pengestrømsbeløb, som er det tilsvarende element i CFListe. Standardværdien er 1. Hvis du indtaster værdier, skal de være positive heltal < 10.000. |
|
|
Katalog > |
|
|
nSolve(Ligning,Var[=Gæt])Þtal eller fejlstreng nSolve(Ligning,Var[=Gæt],nedreGrænse) Þtal eller fejlstreng nSolve(Ligning,Var[=Guess],nedreGrænse,øvreGrænse) Þtal eller fejlstreng nSolve(Ligning,Var[=Guess]) | nedreGrænse{Var{øvreGrænse Þ tal eller fejlstreng Søger iterativt efter en approksimeret reel numerisk løsning af Ligning for dens ene variabel. Angiv variablen som: variabel – eller – variabel = reelt tal For eksempel er x gyldig, og det er x=3 også. |
Bemærk: Hvis der er flere løsninger, kan du anvende et gæt til at finde en partikulær løsning. |
|
nSolve() forsøger at bestemme enten et punkt, hvor residualen er nul, eller to forholdsvis tætte punkter, hvor residualerne har modsatte fortegn, og residualen ikke er for stor. Hvis dette ikke kan opnås med et beskedent antal datapunkter, returneres strengen “Ingen løsning blev fundet.” |
|